Whibox part 1: Indistinguishability Obfuscation posted August 2016

I landed in Santa Barbara in a tiny airplane, at a tiny airport, so cute that I could have mistakenly taken it for an small university building collecting toy aircrafts. Outside the weather was warm and I could already smell the ocean.

A shuttle dropped me at the registration building and I had to walk through a large patio filled with people sitting in silence, looking at their notes or their laptops, in what seemed like comfortable couches arranged in a Moroccan way. I thought to myself "they all seem so comfortable, it looks like they've been here many times". As it turns out, Crypto is taking place in Santa Barbara every year and people have got used to it.

I registered at the desk, then went to my assigned room in these summer-vacant student residences, passing by the numerous faces I will probably see again this coming week. I went to sleep early and woke up the next day for the first workshop: WhibOx.

First, let me say that in theory, workshops are cool. Cooler than conferences, because they are here to teach you something. Crypto conferences are filled with PHD students trying to get their publication ratio (the rule of thumb is 3 good papers accepted at 3 big conferences before defending) and researchers trying to market their papers. (Well, some of them are actually good speakers and care about teaching you something in their 45 minutes time frame.)

Back to our workshop, it is the first ever workshop on whitebox crypto and indistinguishability obfuscation (iO). Pascal Pailier -- the author of the homomorphic cryptosystem -- starts the course with a few words: whitebox crypto is something relatively old/new, but it's starting to rise. There is a clear problem that real companies are trying to solve, and whitebox seems to be the answer. Pailier notes that it's not a concept that is well understood, and the speakers will proove his point again and again later, trying to come up with a different definition. In this blogpost I will summarize the day, if you're interested to see the talks yourself the slides should shortly be uploaded, as well as the videos on the ECRYPT channel.

Amit Sahai - Indistinguishability Obfuscation

Indistinguishability Obfuscation was the first topic to be discussed about. Amit reminded us that iO was quite recent, and aimed towards our modern world attack models: programs are routinely leaked to the adversary, often they are even given directly to the adversary.

For a while, they thought about multi-party computation (MPC), but it was not the answer. This is because it requires some portion of the computation to be completely hidden from the adversary.

In the idea of general purpose obfuscation, every part is known by the adversary. But the adversary can still use the program as he wishes! Amit gives an example where a program would give you a different output if you feed it an integer greater or lesser than some fixed value. By just querying the program an attacker could learn it... So for this to work, you would first need some function/program that is un-learnable by queries.

BGIRSVY2001 showed that the concept of a virtual black box (VBB) is impossible for all circuits. That is, a program that you entirely control, and that is indistinguishable from a black box (you can only see input and output).

But then... there are some contrived "self-eating programs", for which this idea of black box obfuscation is not ruled-out. The idea of these self-eating programs is that you have a program P that takes an input x, and it checks if x is a program equivalent to P itself. If so, it outputs a secret s, otherwise 0. But even these have "explicit attacks" against them. So they define an even weaker definition that is iO: a polynomial slowdown + indistinguishability.

The idea of iO is to bring the best possible obfuscation. The first construction was done in 2013, and surprisingly, it was useful! it was used to resolve long-standing open problems like:

• functional encryption
• deniable encryption
• multi-input FE
• patchable iO
• ...

It's kind of a central hub of crypto, anything you want to do in cryptography (except for efficiency), you can use iO to do it.

But first, if you want to obfuscate something, you need a language! They use a Matrix Branching Program (MBP), which is not a straight forward language at all...

It's a bunch of invertible matrix over \(Z_n\), and the input tells you which matrix in each pair to choose. Then you repeat the same pattern over and over until you reach the last pair.

In the image below you can see the pairs on the right, here let's imagine that you take an input of 3 bits. If the input is 011 you would choose \(M_{1,0}\) then \(M_{2,1}\) and then \(M_{3,1}\). You would then repeat this pattern until you reach the last matrix. The output of your program is the multiplication of all the matrices your input chose.

You can implement a bunch of stuff like that it seems, and here's a XOR:

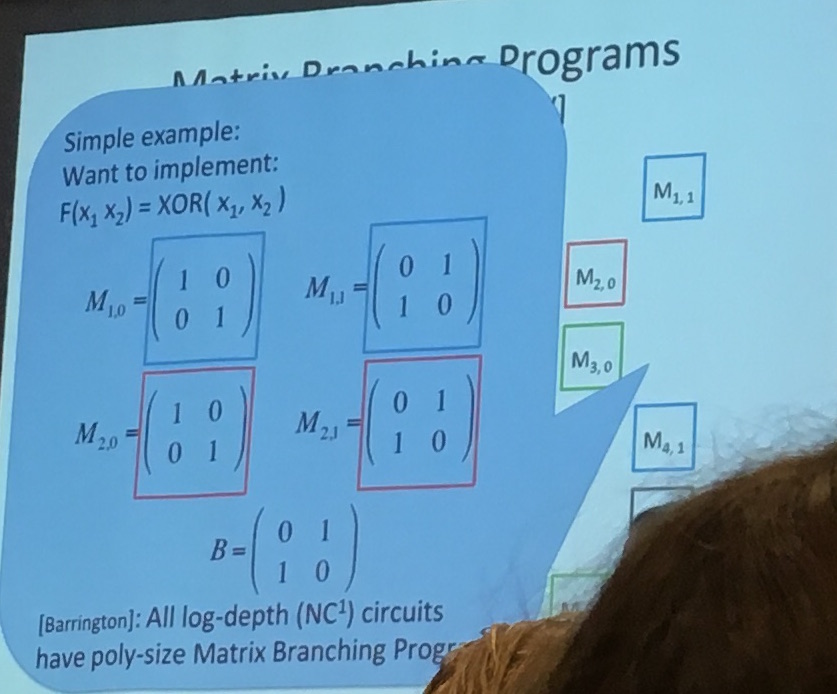
But this is not enough to obfuscate (it's a start). To obfuscate you want to use Kilian randomization: multiply each matrice \(M\) with some \(R\) and its inverse like so: \(RMR^{-1}\).

(slide from a crypto conf)

Now to hide everything you encode the matrices in some way that will still allow matrix multiplications. And for this you use the now famous Multilinear Maps (MMaps) aka Granded Encodings. There are still attacks on that (Annihilation attacks) but new ways to counter against these as well.

But it is still not enough, there are some input-mixing attacks (what if you do not respect the repeating pattern and multiply the wrong matrix), then they can't efficiently bound the information learned by these tricks.

There are of course ways to avoid that... Finally they add some more randomness to the mix... A final construction is made (Miles-Sahai-Zhandry, TTC2016):

They end up using \(3\times3\) matrices instead of the initial matrices to finish the obfuscation. It seems like this technique is making the thing look random, so that the adversary now has to distinguish it from randomness as well.

It's of course confusing and it seems like reading the paper might help more. But the idea is here. A circuit, that is obfuscable according to some definition, is transformed into this MBP language, then obfuscated using an encoding (MMaps) and some other techniques.

It's an incredibly powerful construction, which is still at its infancy stage (they are still exploring many other constructions). And its biggest problem right now is efficiency. Amit talks about a \(2^{100}\) overhead for programs like AES (It's almost as good as the complexity of an attack on AES).

So yeah. Completely theoretical at the moment. No way anyone is going to use that. But they're quickly improving the constructions and they're really happy that they have planted the seeds for a new generation of crypto primitives.

Mariana Raykova - 5Gen: a framework for prototyping applications using multilinear maps and matrix branching programs

The workshop had a lot of speakers, and so a lot of repetions were made. Which is not necessarily a bad thing since it's always good to see new concepts being defined by different persons.

The point of obfuscation for Raykova is to protect proprietary algorithms, software patches and avoid malware detection.

Now, the talk is about Functional Encryption: some construction that allows you to generate decryption keys that reveal only functions of the encrypted message.

They implemented a bunch of stuff. For that they use a compiler (called Cryfms) that transforms Cryptol code ("Cryptol is used mostly in the intelligence community") to a minimal finite state machine and then to Matrix Branching Programs (MBPs). It's called 5gen and it's on github!

Like many speakers at this workshop, she made fun of the efficiency of iO

And then explained again how iO worked. Here you can see the same kind of explanation as Amit did.

Barrington has a construction to convert circuits to MBP, but the bad thing is that the size of the MBP is exponential in the circuit depth. Urg... That's why they transform the Cryptol code in a finite state automata first before converting it to MBP. It's better to transform a finite state automata in a MBP directly:

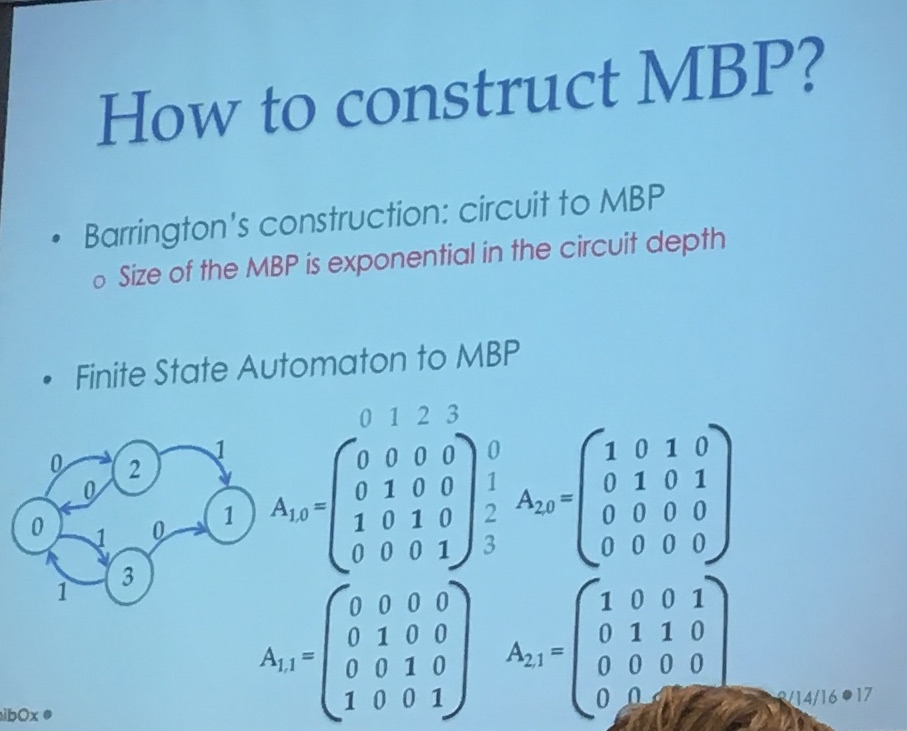
Raykova explained that they used a bunch of optimization, sometimes the second matrix wouldn't change anything (or wouldn't change a part of the state) she said, so they could pre-multiply them...

Now to obfuscate you use Kilian88 to do Randomized branching programs (RBP) as Amit already explained

And as Amit said, this is not enough for obfuscation, you need to apply encoding techniques (MMaps). MMaps gives you a way to encode an element (which is hiding the element), and give you some nice property on the encoding (to do operations).

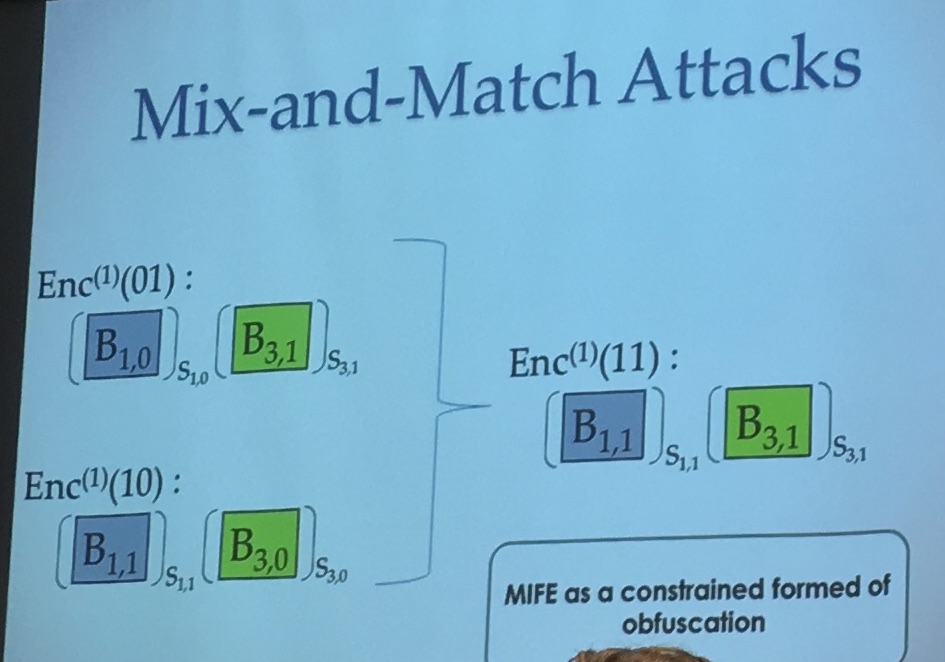
But you still have these mix and match attacks. In the iO model the adversary can use the whole program and feed it all sort of inputs, but in FE we don't want that.

You can read part 2 here