Key wrapping and nonce-misuse resistance posted March 2021

If you know about authenticated encryption, you could stop reading here, understand that you can just use AES-GCM or Chacha20-Poly1305 whenever you need to encrypt something, and move on with your life. Unfortunately real-world cryptography is not always about the agreed standard, it is also about constraints. Constraints in size, constraints in speed, constraints in format, and so on. For this reason, we need to look at scenarios where these AEADs won't fit, and what solutions have been invented by the field of cryptography.

Wrapping keys: how to encrypt secrets

One of the problem of nonce-based AEADs is that they all require a nonce, which takes additional space. In worse scenarios, the nonce to-be-used for encryption comes from an untrusted source and can thus lead to nonce repetition that would damage the security of the encryption. From these assumptions, it was noticed that encrypting a key might not necessarily need randomization, since what is encrypted is already random.

Encrypting keys is a useful paradigm in cryptography, and is used in a number of protocol as you will see in the second part of this book.

The most widely adopted standard is NIST Special Publication 800-38F, Recommendation for Block Cipher Modes of Operation: Methods for Key Wrapping. It specifies two key wrapping algorithms based on AES: the AES Key Wrap (KW) mode and the AES Key Wrap With Padding (KWP) mode.

These two algorithms are often implemented in Hardware Security Modules (HSM). HSMs are devices that are capable of performing cryptographic operations while ensuring that keys they store cannot be extracted by physical attacks. That's at least if you're under a certain budget.

These key-wrapping algorithms do not take an additional nonce or IV, and randomize their encryption based on what they are encrypting. Consequently, they do not have to store an additional nonce or IV next to the ciphertexts.

AES-GCM-SIV and nonce-misuse resistance authenticated encryption

In 2006, Rogaway published a new key-wrapping algorithm called Synthetic initialization vector (SIV), as part of Deterministic Authenticated-Encryption: A Provable-Security Treatment of the Key-Wrap Problem. In the white paper, Rogaway notes that the algorithm is not only useful to encrypt keys, but as a general AEAD algorithm as well that is resistant to nonce repetitions. As you probably know, a repeating nonce in AES-GCM or Chacha20-Poly1305 has catastrophic consequences. It not only reveals the XOR of the two plaintexts, but it also allows an attacker to recover an authentication key and to forge more messages. In Nonce-Disrespecting Adversaries: Practical Forgery Attacks on GCM in TLS, a group of researchers found 184 HTTPS servers being guilty of reusing nonces. (I even wrote here about their super-cool live demo.)

The point of a nonce-misuse resistant algorithm is that encrypting two plaintexts with the same nonce will only reveal if the two plaintexts are equal or not.

It is sometimes hard to obtain good randomness on constrained devices or mistakes can be made. In this case, nonce-misuse resistant algorithms solve real problems.

In the rest of this section, I describe the scheme standardized by Google in RFC 8452, AES-GCM-SIV: Nonce Misuse-Resistant Authenticated Encryption.

The idea of AES-GCM-SIV is to generate the encryption and authentication keys separately via a main key every time a message has to be encrypted (or decrypted). This is done by producing a keystream long enough with AES-CTR, the main key and a nonce:

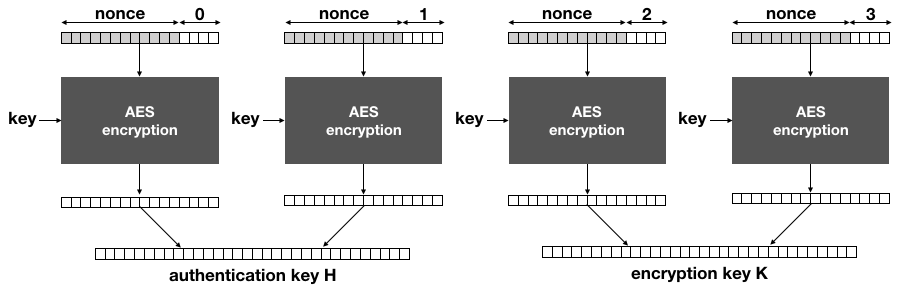
The main key of AES-GCM-SIV is used solely with AES-CTR to derive the encryption key K and the authentication key H.

Notice that if the same nonce is used to encrypt two different messages, the same keys will be derived here.

Next, AES-GCM-SIV authenticates the plaintext, instead of the ciphertexts as we have seen in the previous schemes. This creates an authentication tag over the associated data and the plaintext (and their respective lengths). Instead of GMAC, AES-GCM-SIV defines a new MAC called Polyval. It is quite similar and only attempts to optimize some of GMAC's operations.

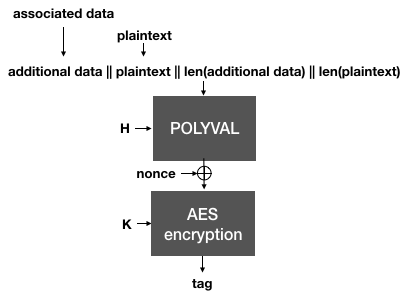
The Polyval function is used to hash the plaintext and the associated data. It is then encrypted with the encryption key K to produce an authentication tag.

Importantly, notice that if the same nonce is reused, two different messages will of course produce two different tags. This is important because in AES-GCM-SIV, the tag is then used as a nonce to AES-CTR in order to encrypt the plaintext.

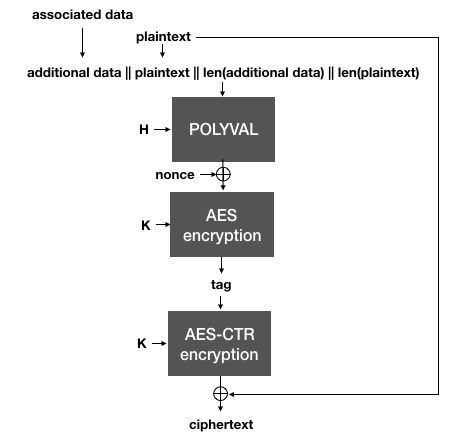
AES-GCM-SIV uses the authentication tag (created with Polyval over the plaintext and the associated data) as a nonce for AES-CTR to encrypt the plaintext.

This is the trick behind SIV: the nonce used to encrypt in the AEAD is generated from the plaintext itself, which makes it highly unlikely that two different plaintexts will end up being encrypted under the same nonce. To decrypt, the same process is done in reverse:

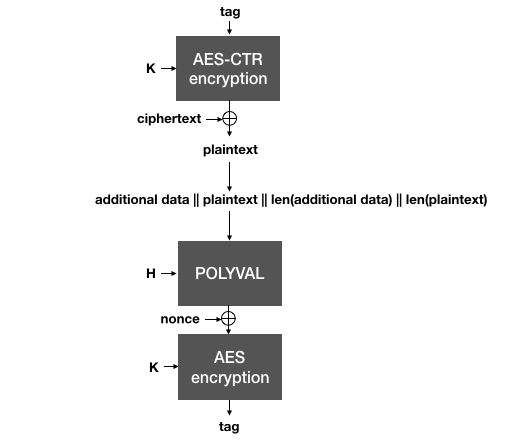
AES-GCM-SIV decrypts a ciphertext by using the authentication as a nonce for AES-CTR. The plaintext recovered is then used along with the associated data to validate the authentication tag. Both tags need to be compared (in constant-time) before releasing the plaintext to the application.

As the authentication tag is computed over the plaintext, the ciphertext must first be decrypted (using the tag as an effective nonce). Then, the plaintext must be validated against the authentication tag. Because of that, one must realize two things:

• The plaintext is released by the algorithm before it can be authenticated. For this reason it is extremely important that nothing is done with the plaintext, until it is actually deemed valid by the authentication tag verification.
• Since the algorithm works by decrypting the ciphertext (respectively encrypting the plaintext) as well as authenticating the plaintext, we say that it is two-pass -- it must go over the data twice. Because of this, it usually is slower than its counterpart AES-GCM.

SIV is a powerful concept that can be implemented for other algorithms as well.