How did length extension attacks made it into SHA-2? posted August 2017

If you don't know about length extension attacks, it is a very simple and straight forward attack that let you forge a new hash by extending another one, letting you pretend that hashing had previously not been terminated.

The attack targets such hashes: SHA-256(key | message) where the key is secret and where | means concatenation.

This is because a SHA-2 hash (unless we're talking about the truncated versions) is literally a full copy of the state of the hash. It is not the state of hashing key and message, but rather key and message and some padding. Because like everything in the symmetric crypto world you need to pad to the block size. I believe this is 512 bits in the Secure Hash Algorithm 2.

The attack lets you take such a hash, and continue the hashing to obtain the hash of key | message | padding | more where more is whatever you want. And all of this without any knowledge of the secret key!

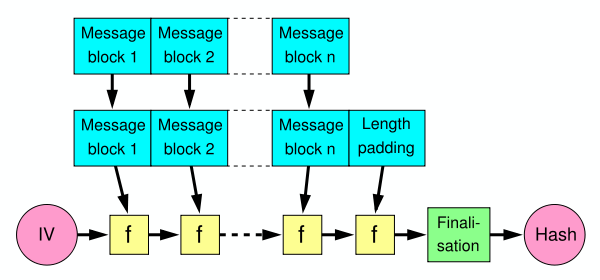
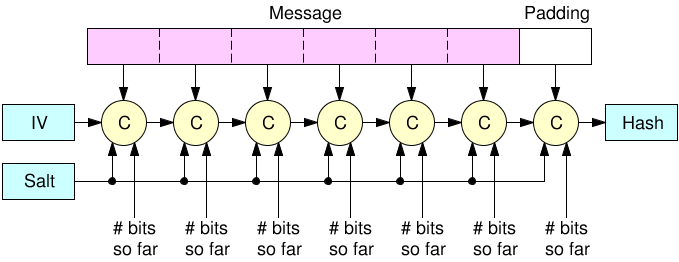
Interestingly, this comes from the way the Merkle-Damgard construction is applied (without a good finalization function). And because of this hash functions like MD4, MD5, SHA-1 and SHA-2 have all suffered from the same issues. You'd be glad to hear that this issue is fixed in any of the SHA-3 contestant (read: BLAKE2 and SHAKE and SHA-3 are fine). Keccak (SHA-3's winner) fixes it by using a Sponge construction, not letting you see a big part of the state (the capacity) while BLAKE2 fixes it by using the HAsh Iterative FrAmework (HAIFA), using a "number of bits hashed so far" (not including the padding) inside of the compression function.

While looking at the exact date length extension attacks were found (which I couldn't find), Samuel Neves came up with an interesting response.

It looks like the NIST was made aware, during the standardization process of SHA-2, that simple fixes would prevent length extension attacks.

This comment from John Kelsey (who later joined the NIST) is from 28 august 2001 (by the way it doesn't make sense to write dates as month/day/year. Nobody can understand it outside of the US. We have an ISO format that specifies a logical year-month-day). In it he talks about the attack, and proposes a simple fix:

Niels Ferguson suggested the following simple fix to me, some time ago: Choose some nonzero constant C0, of the same size as the hash function chaining variable. Hash messages normally, until we come to the last block in the padded message. XOR C0 into the chaining variable input into that last compression function computation. The resulting compression function output is used as the hash result. For concreteness, I propose C0 = 0xa5a5...a5, with the 0xa5 repeated until every byte is filled in. This should be interpreted in little-endian bit ordering.

Why did the NIST ignore this when it could have modified the draft before publication? I have no idea. Is this one more fuck up from their part?