About Disco (again) posted October 2018

I was in Milan two weeks ago presenting on Disco at Advances in permutation-based cryptography. I prepared a few figures to show the current state of Disco.

The funny one is this realistically proportional figure where the areas of the different circles are representing the number of lines-of-code of each libraries.

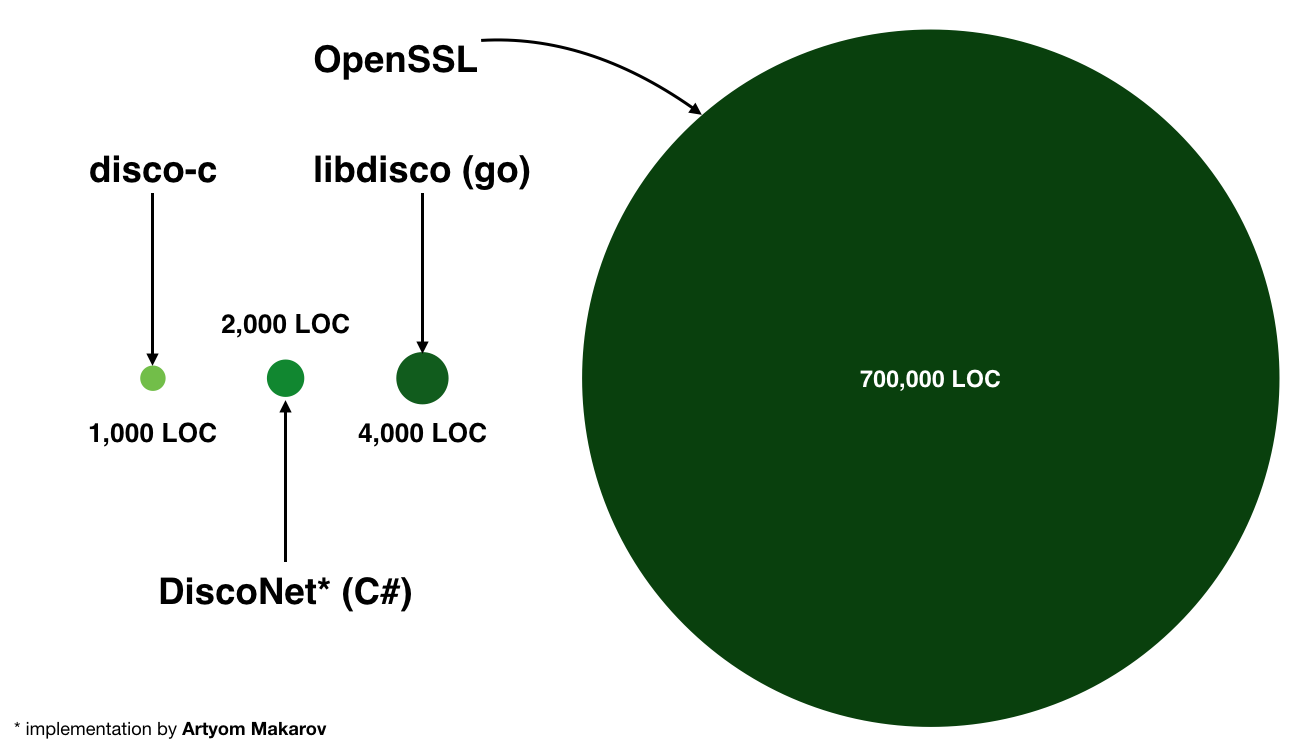
The C library is currently awful, so I won't link to it until I get it to a prettier place, but as a proof of concept it shows that this can be achieve in a mere 1,000 lines-of-code. That while supporting the same functionalities of a TLS library and even more. The following diagram is the dependency graph or "trust graph" of an implementation of Disco:

As one can see, Disco relies on Strobe (which further relies on keccak-f) for the symmetric cryptography, and X25519 for the asymmetric cryptography. The next diagram shows the trust graph of a biased TLS 1.3 implementation for comparison:

This was done mostly for fun, so I might be missing some things, but you can see that it's starting to get more involved. Finally, I made a final diagram on what most installations actually depend on:

In this one I included other versions of TLS, but not all. I also did not include their own trust graph. Thus, this diagram is actually less complex that it could be in reality, especially knowning that some companies continue to support SSL 3.0 and TLS 1.0.

I've also included non-cryptographic things like x509 certificates and their parsers, because it is a major dependency which was dubbed the most dangerous code in the world by M. Georgiev, S. Iyengar, S. Jana, R. Anubhai, D. Boneh, and V. Shmatikov.