What's my birthday? posted September 2019

My colleague Mesut asked me if using random identifiers of 128-bit would be enough to avoid collisions.

I've been asked similar questions, and every time my answer goes something like this:

you need to calculate the number of outputs you need to generate in order to get good odds of finding collisions. If that number is impressively large, then it's fine.

The birthday bound is often used to calculate this. If you crypto, you must have heard of something like this:

with the SHA-256 hash function, you need to generate at least 2¹²⁸ hashes in order to have more than 50% chance of finding collisions.

And you know that usually, you can just divide the exponent of your domain space by two to find out how much output you need to generate to reach such a collision.

Now, this figure is a bit deceiving when it comes to real world cryptography. This is because we probably don't want to define "OK, this is bad" as someone reaching the point of having 50% chance of finding a collision. Rather, we want to say:

someone reaching one in a billion chance (or something much lower) to find a collision would be bad.

In addition, what does it mean for us? How many identifiers are we going to generate per second? How much time are we willing to keep this thing secure?

To truly answer this question, one needs to plug in the correct numbers and play with the birthday bound formula. Since this is not the first time I had to do this, I thought to myself "why don't I create an app for this?" and voila.

You can play with it here.

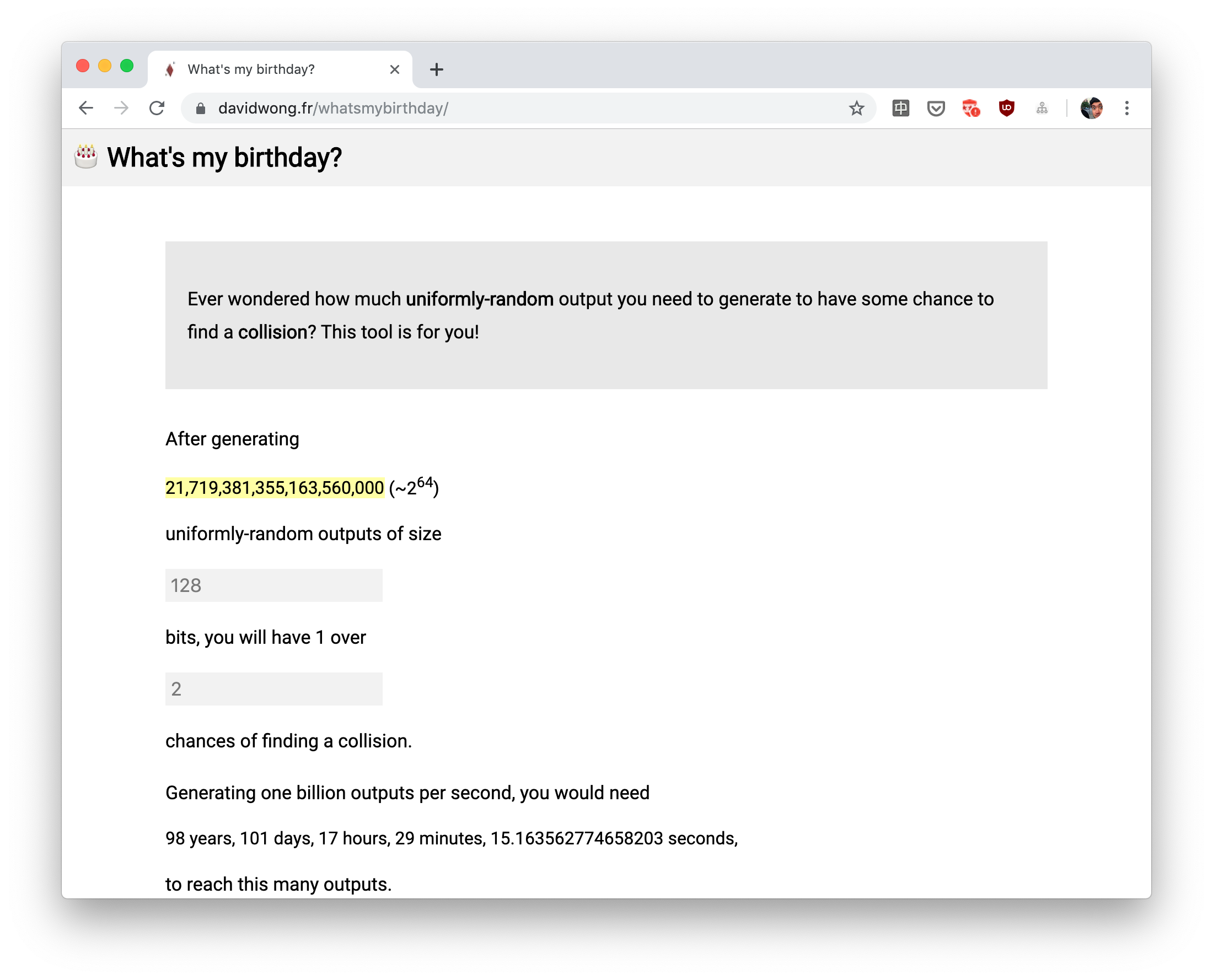
Thanks to my tool, I can now answer Mesut's question:

If you generate one million identifiers per second, in 26 years you will have one in a billion chance to generate a collision. Is this enough? If this is not adversary-controlled, or it is rate-limited, you will probably not generate millions of identifiers per second though, but rather thousands, in this case it will take 265 centuries to get these odds.