''This destroyes the RSA cryptosystem'' posted March 2021
Schnorr just released a new paper Fast Factoring Integers by SVP Algorithms with the words "This destroyes the RSA cryptosystem." (spelling included) in the abstract.
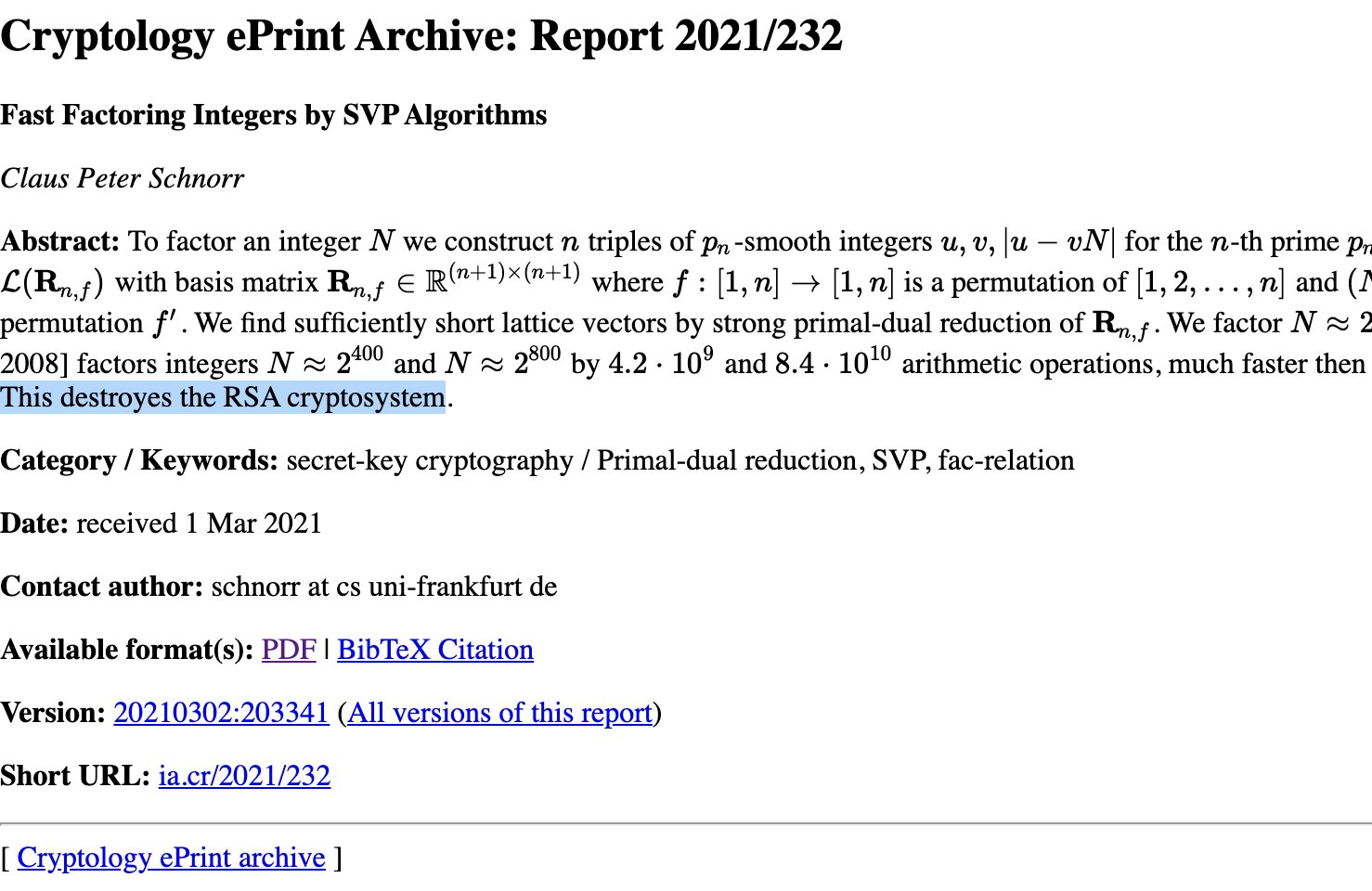
What does this really mean? The paper is honestly quite dense to read and there's no conclusion in there.
UPDATE: Several people have pointed out that the "This destroyes the RSA cryptosystem" is not present in the paper itself, that is until the paper was updated to include the sentence without the typo.
UPDATE: There was some discussion about a potential fake, but several people in the industry are confirming that this is from Schnorr himself:
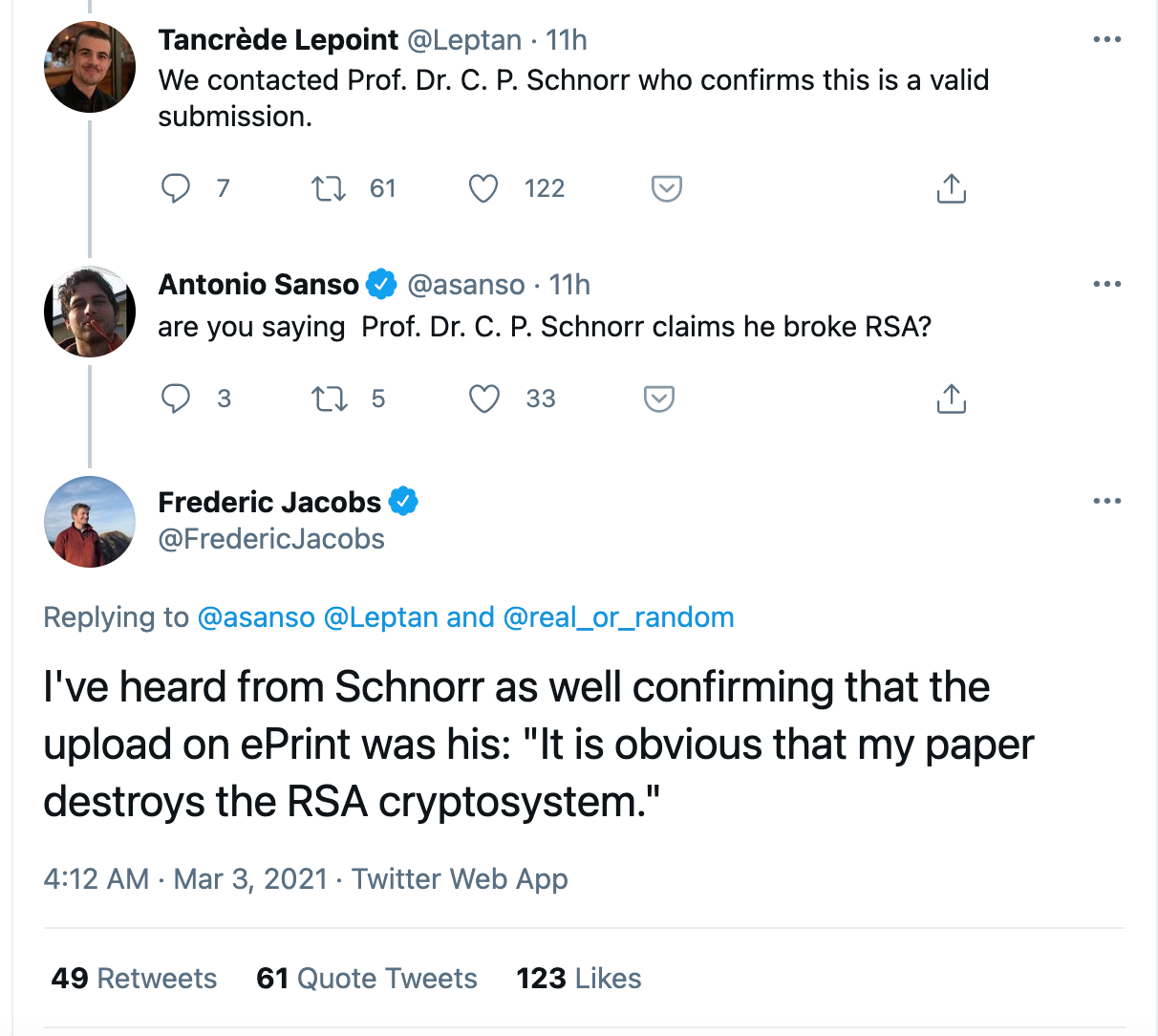
UPDATE: Sweis is calling for a proof of concept:
According to the claims in Schnorr’s paper, it should be practical to set significant new factoring records. There is a convenient 862-bit RSA challenge that has not been factored yet. Posting its factors, as done for the CADO-NFS team’s records, would lend credence to Schnorr’s paper and encourage more review of the methodology.
UPDATE: Léo Ducas has been trying to implement the claim, without success.
UPDATE: Geoffroy Couteau thinks the claim is wrong:
several top experts on SVP and CVP algorithms have looked at the paper and concluded that it is incorrect (I cannot provide names, since it was in the context of anonymous reviews).
UPDATE: Daniel Shiu pointed out an error in the paper
UPDATE: Pedro Fortuny Ayuso is very skeptical of the claim. Will he end up eating his shirt?
Schnorr is 78 years old. I am not gerontophobic (being 50 I am approaching that age) but: Atiyah claimed the Riemann Hypothesis, Hironaka has claimed full resolution of singularities in any characteristic... And I am speaking of Fields medalists. So: you do really need peer-review for strong arguments.


Comments
Richard Harris
In mathematics, when one reads something that is reasonably clear, there are two routes to take:
1. trash it entirely without reserve when there is no idea, only so called "mathematics"
2. assume it correct when the idea shows its originality, and then carefully vet the details
As pertaining to Schnorr's FFIBSA (Fast Factoring Integers by SVP Algorithms), my opinion is definitely the latter category. In other words, unless details show some kind of real miss, RSA can be considered destroyed.
I am almost, I repeat almost, ignorant in this regard, but just some personal feeling.
To me, there is only ONE issue to be clarified:
What is or could be the (suspected) degradation of the probability (assuming any reasonable distribution) of finding the "fac-relations" (as the "composite of exactly two" grows in size)?
There have been ample brilliance shown over the announcement of Schnorr, some are mathematical in nature, others are not even wrong.
First, about some non-math stuff.
1. Is it reasonable to not take FFIBSA seriously? It is a slightly difficult question. Normally, one does not take a person such as Schnorr lightly. But looking at the way this is announced, mis-upload, typos, a good mixture of Deutch and English, it does give one the impression of casual treatment. On the other hand, we all make such mistakes. But even going easy on the age of 78, I do think this can easily leave people with some undesirable impression. Maybe, Schnorr was in a hurry to announce? We can only speculate unless we hear from him directly. It really shouldn't happen that way.
2. The comparison between Schnorr and Atiyah is "apples and oranges". For a proof of RH, there is hardly any room for even the slightest inaccuracy. However, there is great lax in the breaking of a security system. You simply do not need to be exactly exact to render a security system "broken". A security system is not defined as, for example, our ability to "easily" double the key length. One is destroyed if the assumption(s) made for its security is shown kaput (surprises beyond your security parameters). When Arjen Lenstra, for example, found a collision based on Wang's findings, would MD5 be considered broken? Would Arjen have to forge every signature there is (or every that a clueless challenges him with)? It is normal brain's knowledge that a _non-negligible_ chance of failure hoses the system. Or am I wrong? Patches, please?
Sometimes, it may not be the failure of a/the system. It could be the end of an entire concept.
3. The age issue is ill-placed as well. There is no (and cannot be) proof, though highly plausible, that with the progress of age fresh insight is less likely. Therefore, to be able to prove RH may be much less likely at older ages than otherwise. But application of LLL, to me, is exactly the opposite. The more experience, the better chance.
Now, a bit more math-inclined. Let me be specific (which is made easy as the issues raised are ACTUALLY mostly reflected here)!
4. "Calling for a proof of concept" may be a good idea, but not quite appropriate here. As mentioned above, if the idea is valid, you won't find composites stand as they did. Verification just does not add anything much. We should first read/understand the basic idea. Proof of concept, in computer science application jargon perhaps, is low level.
5. Leo Ducas's runs without success: work as designed. Read comment by Huck Bennet (this link please: https://twitter.com/DucasLeo/status/1367367057055109125). Nothing after Huck's comment so far. What is f, please? We can always feel superb while being much less so.
6. Keegan Ryan (link: https://twitter.com/inf_0_/status/1367376526300172288?fbclid=IwAR19Ip7XyoPjHfm9WBzqiUkQpxUVLGfVTgLGQmmncgrkUsvcLIrkzbOPw_U) got the two (2^1600 and 0.002) together. Does anybody know what was being talked about? I am perhaps dumb enough to not be able to tell det from the values in a matrix/basis. Where did the 2^200 come from? Schnorr makes a mistake like that? You more than surprised me. What size of the numbers are we looking at most of the time? How do the numbers blow up the complexity (even if we are talking about 1600-bit ones)? Can somebody ask Arjen Lenstra about his multi-precision C-package (developed while he was at Visa), to get an idea of what can be contributed to the exponent (of the overall complexity)? Multiplication is only sub-O(n^2), right?
7. Geoffroy Couteau mentioned experts. What experts? As far as I know, there are only two. One is Andrew Odlyzko (and the other, I am afraid to mention his name). What experts? Irresponsible rumor before rigorous conclusions?
8. I am not going to point to each source. All may be similar to this seemingly baseless thing of factorial (instead of n(n+1)/2). Guys, isn't it only the the diagonal? Where is the factorial?
My math is lousy and am not knowledgeable in this area. But I am really confused by the apparent crap all around.
I admit that I am not too sure of the ease in finding the "fac-relation". Peter gave some idea (such as the rho probability) and I seem to get the impression that the relation is easily found. I am not too sure. But that, as I said, may perhaps be the only thing we need clarification. It is quite possible that Schnorr missed something crucial. But keep in mind: a non-negligible chance of failure is the end of the story.
Apologies for any error and/or misunderstanding on my part.
John Nix
This paper, if passing peer review and also reproducible, is significant for the combination of Schnorr's algorithm with a quantum computer:
https://arxiv.org/pdf/2212.12372.pdf
Basically, a quantum computer is applied with a "quantum approximate optimization algorithm (QAOA)" to "We take advantage of QAOA to optimize the most time-consuming part of Schnorr’s algorithm to speed up the
overall computing of the factorization progress". I can't speak to the details, but it could be important.
leave a comment...