Kimchi: The latest update to Mina's proof system posted March 2022

I initially posted this on https://minaprotocol.com/blog/kimchi-the-latest-update-to-minas-proof-system

(photo taken from https://unsplash.com/photos/M_mDgb8guhA)

We recently released an update to our proof system for Mina called Kimchi. Kimchi is the main machinery we use to generate the recursive proofs that allow the Mina blockchain to remain of a fixed size of 22KB. It will also soon enable privacy and local execution of smart contracts with our snapps update. In this post, we'll go through what Kimchi is and what's different about it.

First, it is good to see where in the stack we are. Looking at the edge of the network, what we can see is a big blackbox: Mina.

If you're curious enough, you can open it and see what's inside. At some point you'll end up with pickles. Pickles is the recursion layer, it is the protocol that we use to create proofs of proofs of proofs of ... and reduce the blockchain to a fixed-size of under 22KB.

Pickles need something to create proofs though, and this is what Kimchi is:

In this post, we'll attempt to create some abstractions and simplifications to teach intuitions about what Kimchi is. We will try to keep explanations at a relatively high level, so it will be up to you to open the blackboxes that we will lay before you.

One of these black boxes, for example, are the pasta curves.

There's clearly a theme here. All that's left is to change Mina's name to another pickled condiment.

A bit of context

Kimchi is based on PLONK, a proof system released in 2019 by Ariel Gabizon, Zachary J. Williamson, and Oana Ciobotaru. Since then, many ameliorations and extensions have been proposed. There's been fflonk, turbo PLONK, ultra PLONK, plonkup, and recently plonky2. It's hard to follow, but essentially all these protocols implement variants of PLONK. Thus, we call them plonkish protocols. Kimchi is such a plonkish protocol.

Today, PLONK is regarded as one of the most ambitious general-purpose zero-knowledge proof constructions. Many projects like Zcash, Polygon Zero (formerly known as Mir Protocol), Aztec network, Dusk, MatterLabs (zksync), Astar, and anoma, have their own implementation of the proof system.

But first, what is a proof system?

Let's look at a scenario that should shed some light on the construction's interface. If you understand this section, you're halfway there, as you'll be able to think for yourself on how general-purpose zero knowledge proofs can be used without having to figure out what's going on inside of it.

Let's imagine that Alice has a sudoku puzzle. She sends it to Bob, and Bob finds a solution to the puzzle. To prove it to her, he sends her the solution.

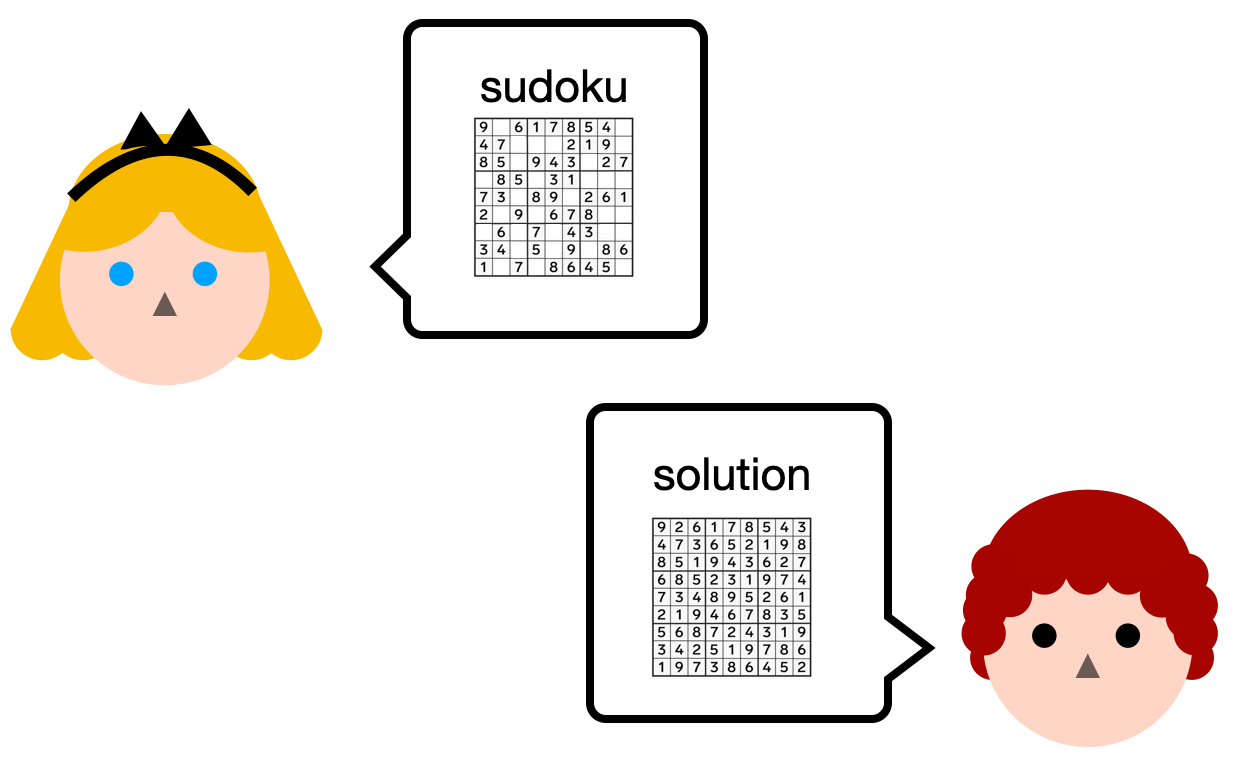
Alice can then run the solution, with the sudoku, in a program that will return true if the solution is correct.

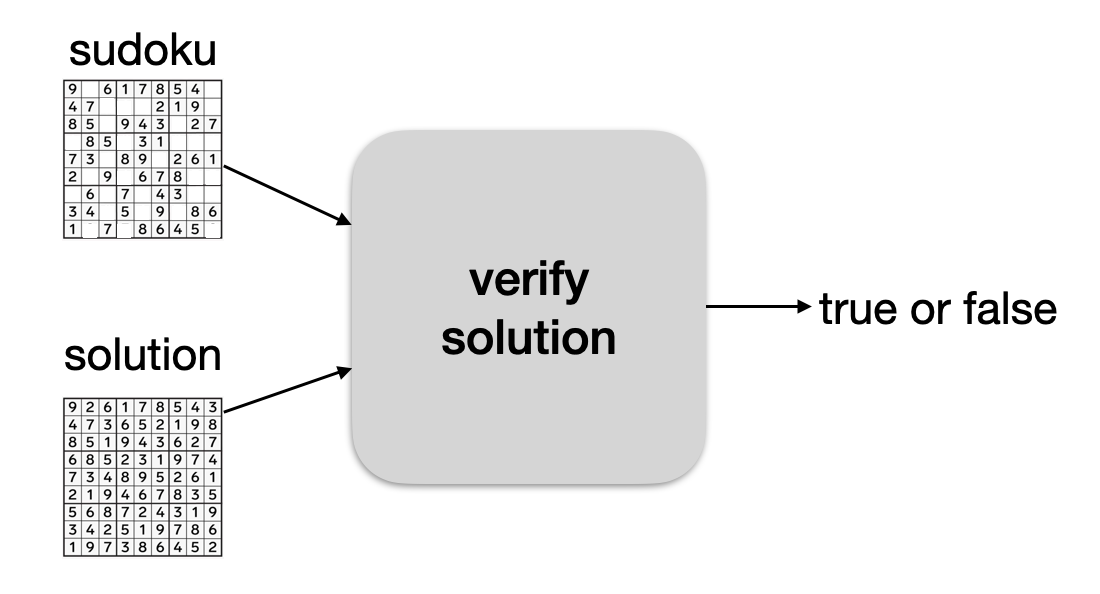
The problem is that Bob doesn't really want to share his solution... So instead, he runs the program himself, on his laptop, and tells Alice "I know a solution, trust me, I just ran the verify solution program on my laptop and it returned true".

Obviously Alice has no reason to trust Bob. We're in a bit of a pickle. This is where protocols like PLONK can be useful. The first step is to take our verify solution program in a special format (I'll come back to that later) and compile it down to two distinct blobs of data:

• the prover index (sometimes called the prover key, although it's not a real key)
• the verifier index (sometimes called the verifier key, not a key either)

Then the prover (Bob) can use a prove algorithm with the prover index, the sudoku puzzle, as well as his solution to execute the program and produce a proof of correct execution (a proof that the program returned true in this case).

We call the sudoku the public input, as it is known by others (like Alice), and the solution the private input, as Bob wants it to remain secret.

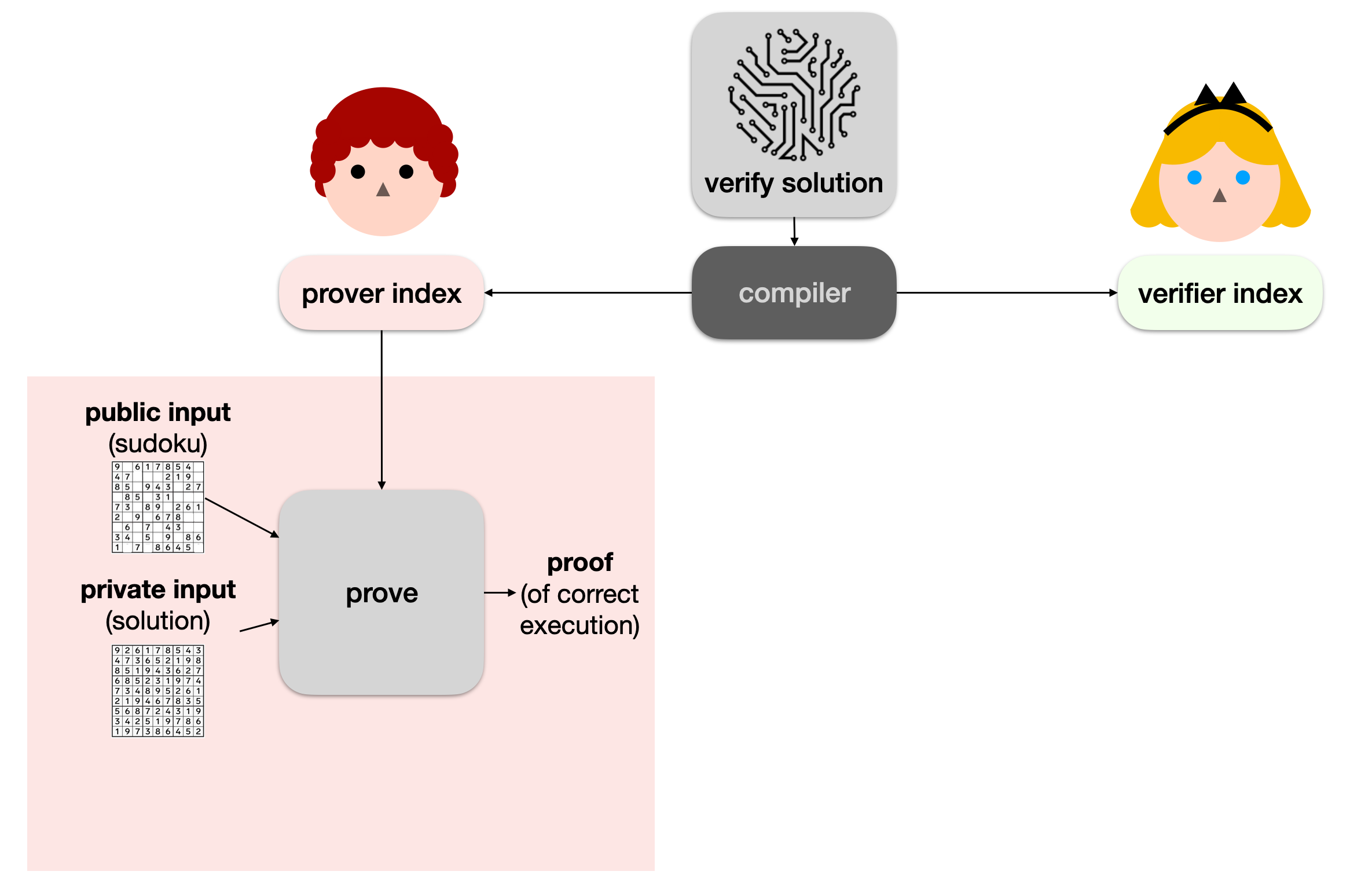
Note: here we don't really care about the output (we just want the program to correctly run to completion, which is equivalent to returning true). Sometimes though, we do care about having a public output (perhaps the result of the execution, which Alice can use). In these cases, the public output is part of the public input. (This detail doesn't really matter in practice.)

Now, Bob can simply give the proof to Alice, and Alice can verify it with another algorithm called verify. If the verify function returns true, she knows that Bob correctly ran the program verify solution to completion (using her sudoku puzzle and his solution).

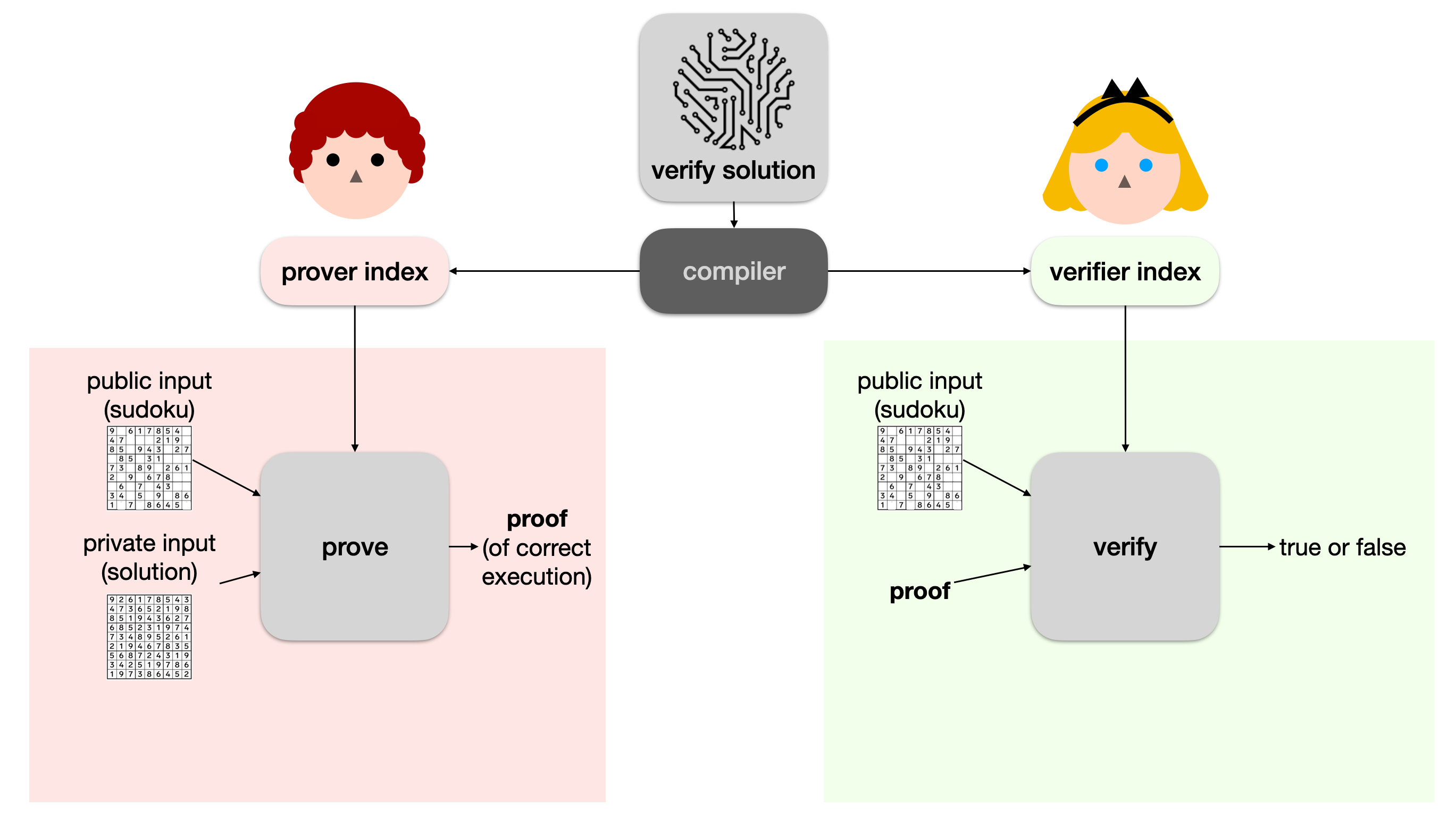
What about Snapps?

In Mina, snapps (zero-knowledge smart contracts) can be written in typescript using the snarkyjs library, and then compiled down to some intermediary representation with snarky. A Kimchi compiler can then be used to compile the program into the prover and verifier indexes, and both sides can use Kimchi provided functionalities to produce proofs as well as verify them.

The verifier index is uploaded on chain, which allows anyone to verify proofs contained in transactions that claim that they executed a snapp correctly.

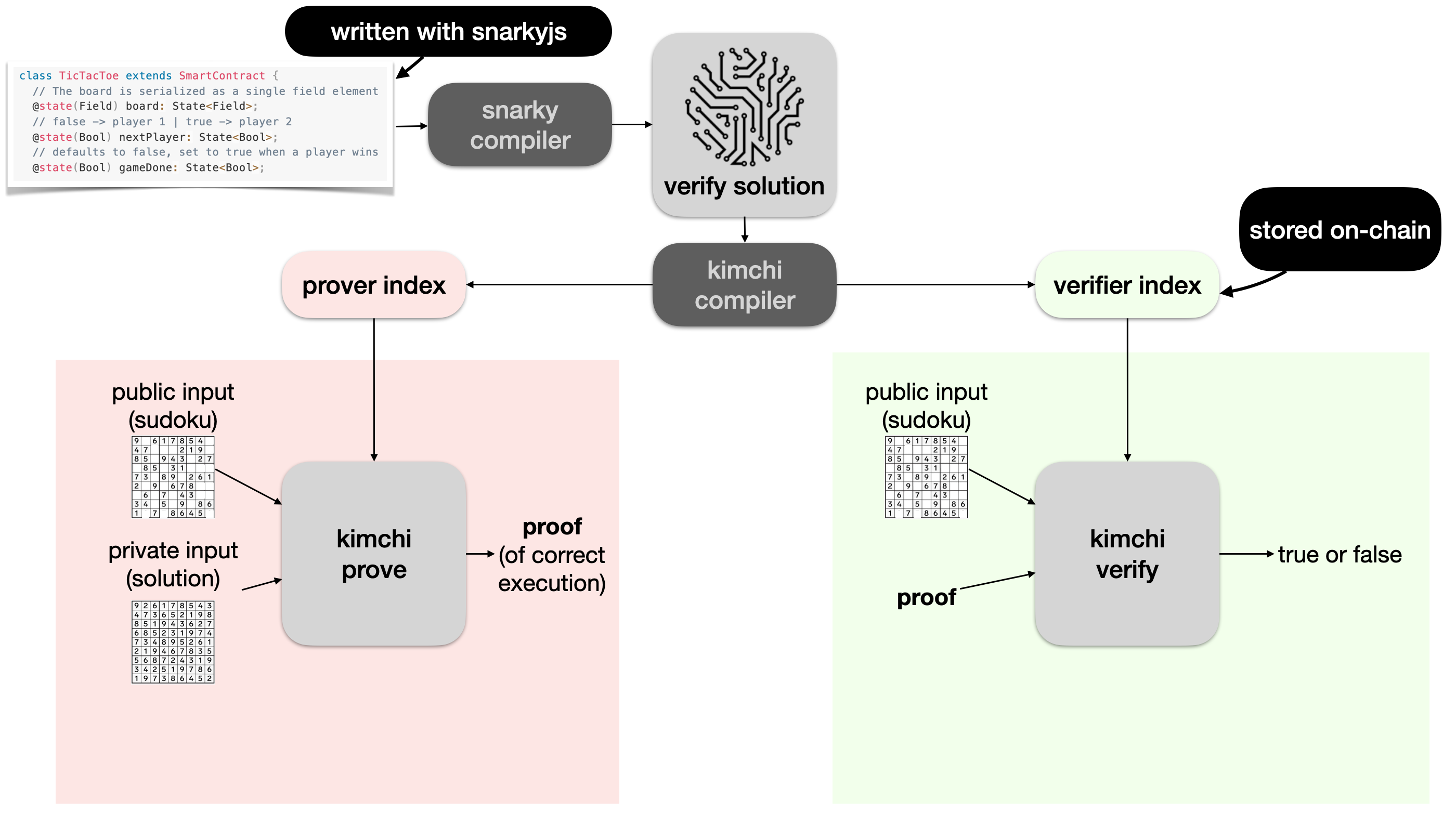
Arithmetic circuits

Let's now address the elephant in the room: cryptography is about math and numbers, but programs like our sudoku solution verifier are about instructions and bits. That's not going to work. What can we do about it? The solution is to use arithmetic circuits!

Arithmetic circuits are circuits made out of arithmetic gates:

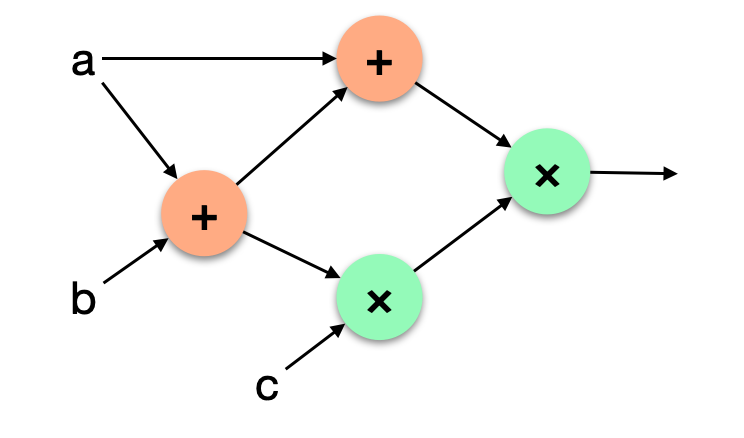
I'll argue that with an addition gate (that adds two numbers together) and a multiplication gate (that multiplies two numbers together) we can rewrite most programs.

Let's look at a simple example. Let's imagine that I want to use a bit x in a computation. To do that, I first need to make sure that x is indeed a bit (that it is 0 or 1).

Look at the following equation: x(x-1) = 0. This should be true, only if x is 0 or 1. We call that a constraint (we're constraining x to some values). Writing circuits for our proof system is about writing such constraints. Many of them in fact.

Let's see how that works with our arithmetic gates.

First we add 1 to -x (I'll explain how to get -x from x later). Then we use the multiplication gate with the output:

The output of the multiplication gate must be 0 (that's the constraint we want to write).

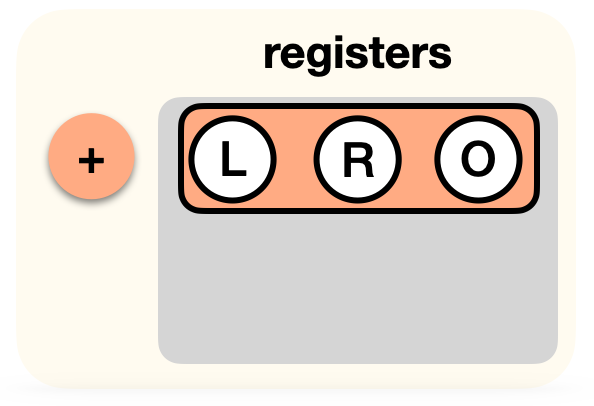
This is it, our circuit for now only has two gates. In PLONK, you would write this down as a list of gates acting on registers (the two inputs L and R, and the output O):

Now, we aren't really doing an addition of L and R here, we're rather adding 1 to -R. How do we do this? Perhaps we could have a "add with constant" gate, and a "subtract gate"? Instead, we "tweak" our addition gate:

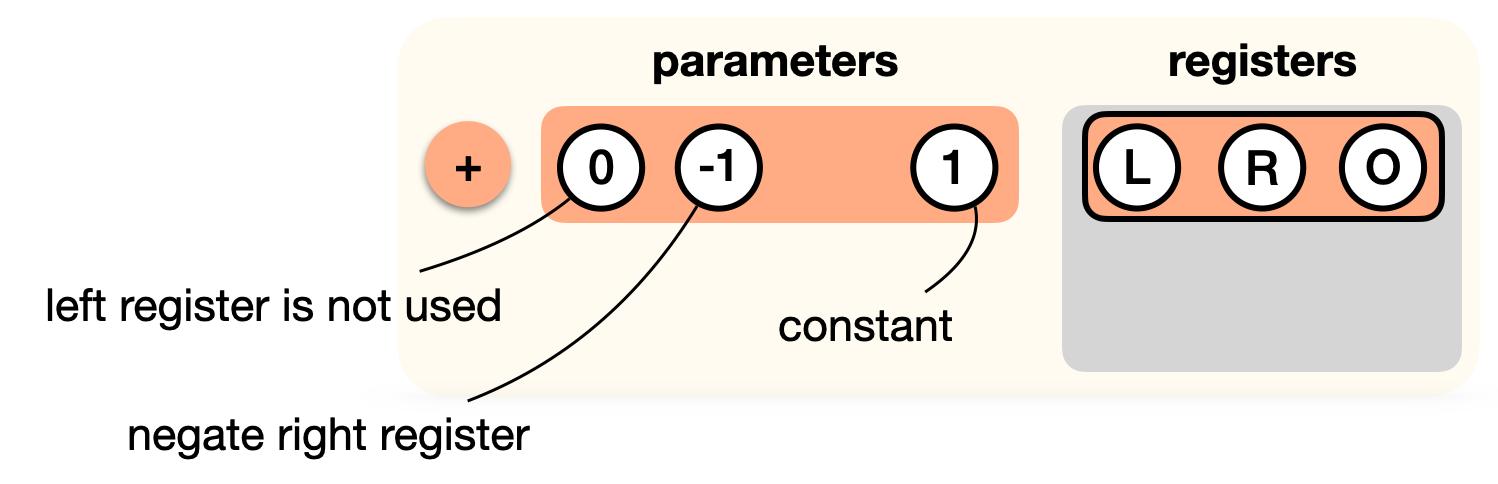
Now let's add the multiplication gate to the list. But remember, the output register is not used, as it must be 0. So we tweak that gate as well:

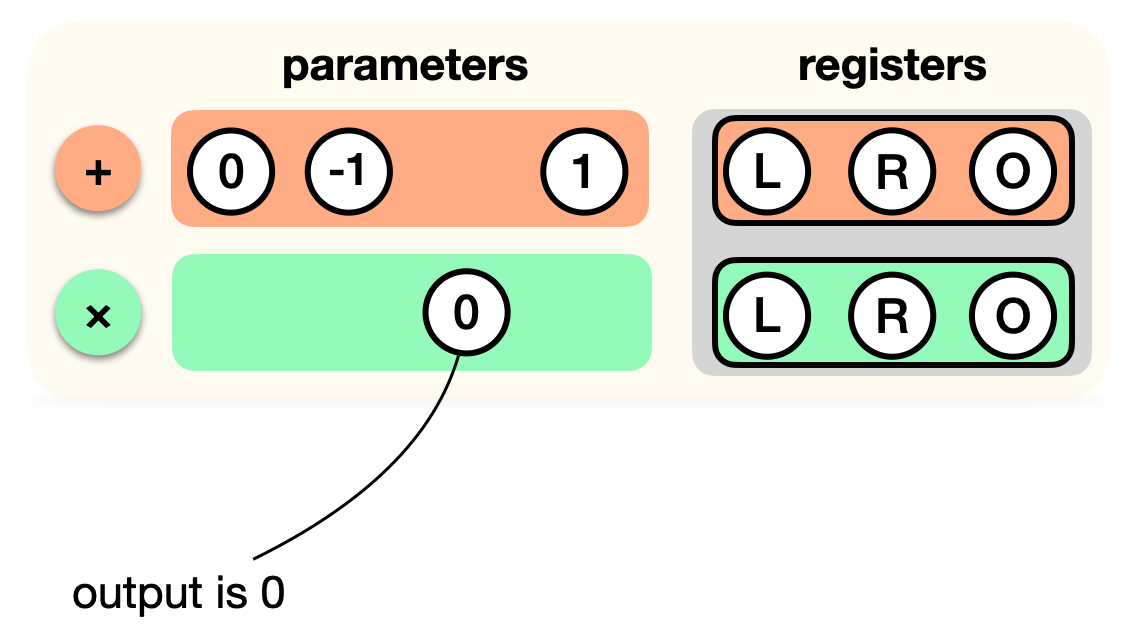
More on tweaking these gates later.

There's one last thing that we're missing: the output register of the first gate is the left register of the second gate. We can simply wire the two registers to encode this correspondance:

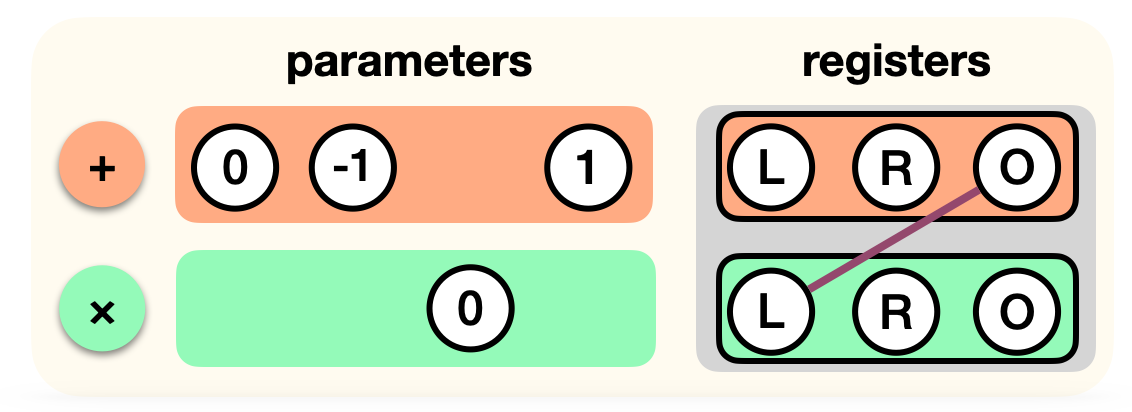
And this is how we represent a circuit in PLONK! We just list all the gates (and their parameters) as well as the wiring between the registers they act on.

Now, when a prover wants to produce a proof, they will run the program and record the values of each registers in an execution trace. For example, here is one that takes x = 0.

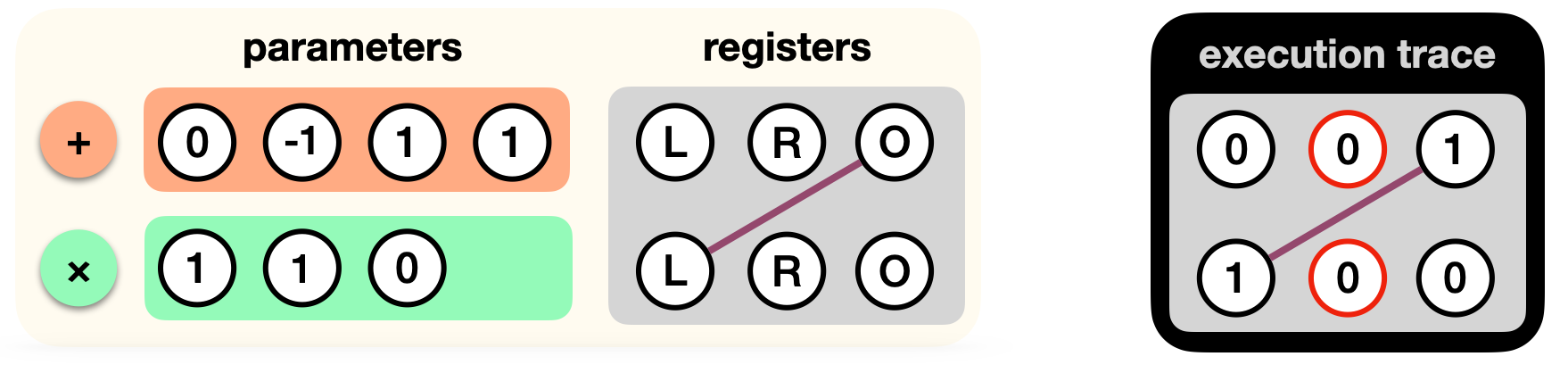
Note: the values in the left register of the first gate, and the output register of the second gate, can be anything as they are not used by the gates.

One simplification I made, is that we don't know where x comes from here. In a real circuit, the right registers of this execution trace are wired to another register containing the value x (or perhaps it is given as private or public input to the circuit, but I will avoid explaining how this works here).

Another simplification I made, is that in reality the addition and multiplication gates are implemented as a single tweakable gate that we call the generic gate in Kimchi:

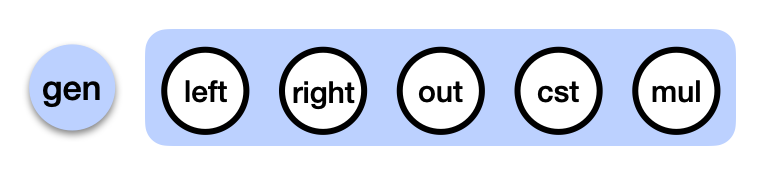
Tweaking the parameters of the generic gate essentially turns it into different gates (addition, multiplication, addition with constant, subtraction, etc.)

From PLONK to Kimchi

Kimchi is a collection of improvements, optimizations, and alterations made on top of PLONK. For example, it overcomes the trusted setup limitation of PLONK by using a bulletproof-style polynomial commitment inside of the protocol. This way, there is no need to trust that the participants of the trusted setup were honest (if they were not, they could break the protocol). Talking about circuits, since we're talking about circuits here, Kimchi adds 12 registers to the 3 registers PLONK already had:

These registers are split into two types of registers: the IO registers, which can be wired to one another, and temporary registers (sometimes called advice wires) that can be used only by the associated gate.

More registers means that we now can have gates that take multiple inputs instead of just one:

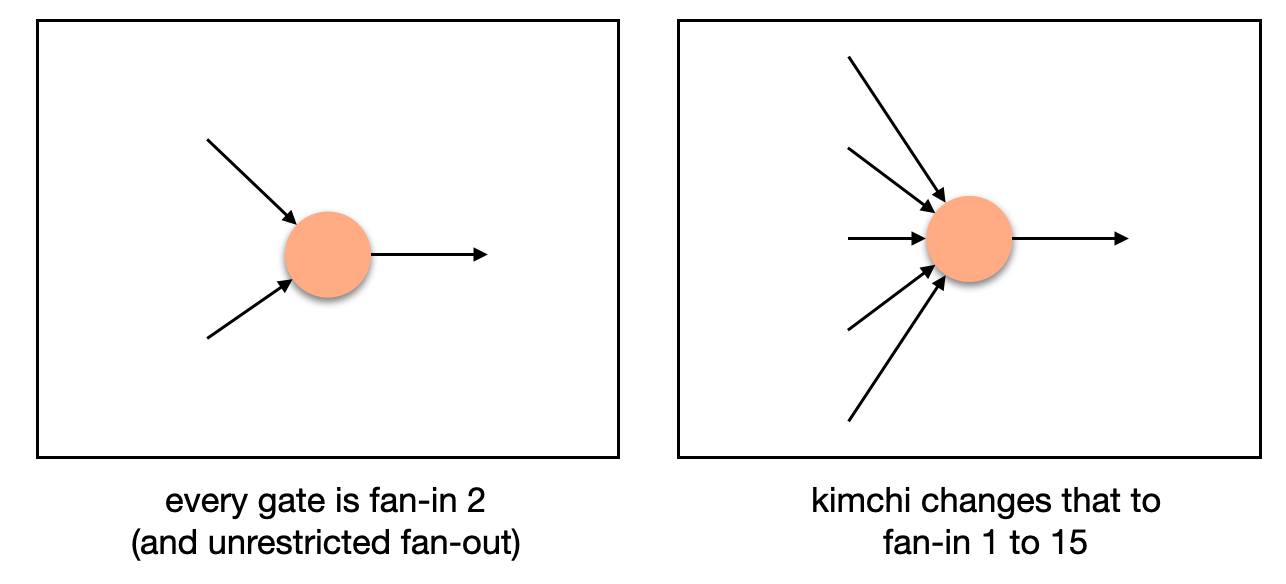
This opens new possibilities. For example, a scalar multiplication gate would require at least three inputs (a scalar, and two coordinates for the curve point). As some operations happen more often than others, they can be rewritten more efficiently as new gates. Kimchi offers 9 new gates at the moment of this writing:

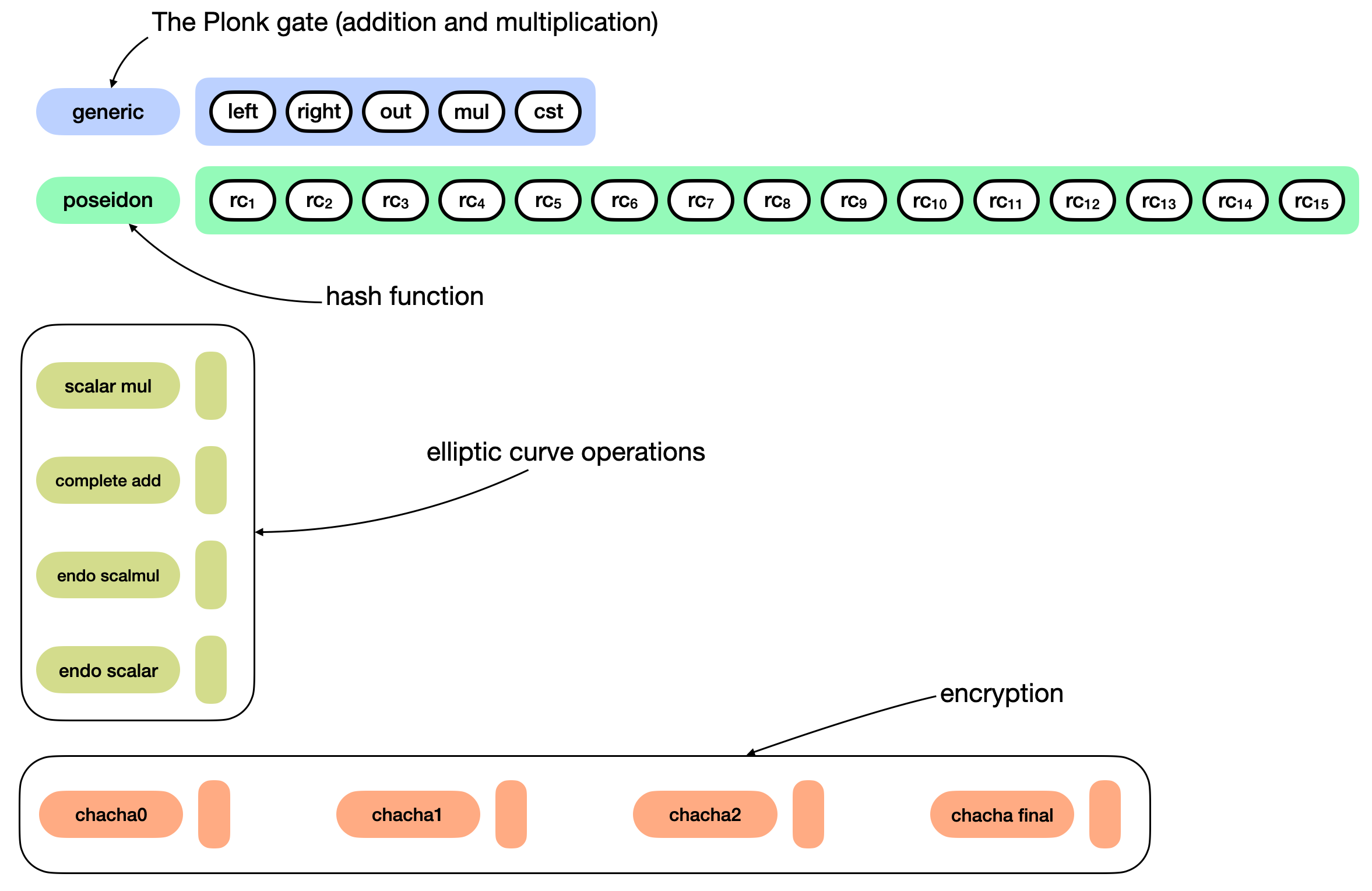
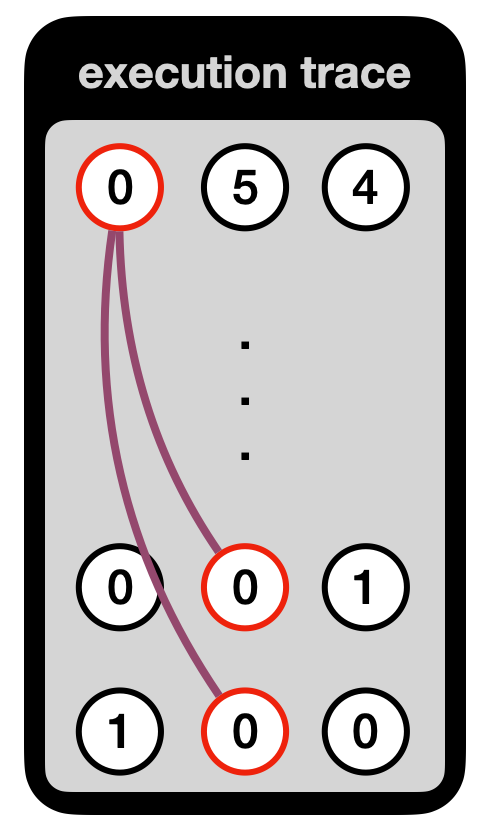
Another concept in Kimchi is that a gate can directly write its output on the registers used by the next gate. This is useful in gates like "poseidon", which need to be used several times in a row (11 times, specifically) to represent the poseidon hash function:

Another performance improvement implemented in Kimchi are lookups. Sometimes, some operations can be written as a table. For example, an XOR table:

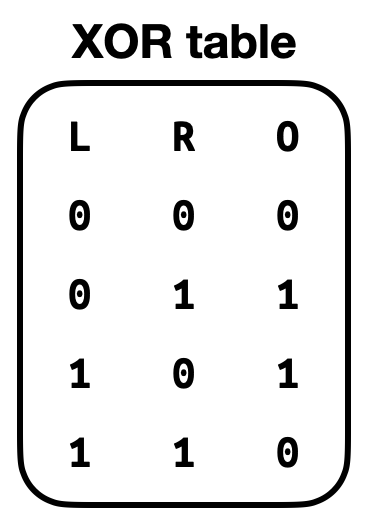
An XOR table for values of 4 bits is of size 2⁸. Implementing this with generic gates would be hard and lengthy, so instead Kimchi builds the table and allows gates (so far only Chacha uses it) to simply perform a lookup into the table to fetch for the result of the operation.

There's much more to Kimchi, but this is for another time. You can check out the implementation here and if you're curious opening the other blackboxes you can check our our in-depth explanations here.

To summarize

Pickles now uses an upgraded proof system: Kimchi. Kimchi brings several optimizations and quality-of-life improvements to circuit builders. This should allow for faster provers, larger circuits, and potentially shorter proof sizes!