Quick access to articles on this page:
more on the next page...
I spent some days over Christmas to read the paper Cairo – a Turing-complete STARK-friendly CPU architecture. First, it's a work of art. I find a lot of the papers in the field of general-purpose zero-knowledge proofs (GP-ZKPs) quite hard to read, but this one has a lot of emphasis on the flow and on examples. More than that, the ideas contained in the paper are quite mind-blowing (although everything is mind-blowing in the land of GP-ZKPs).
What is this paper? It's the layout, in quite the detail, of a protocol that can be used to produce zero-knowledge proofs that a program executed correctly (what they call proof of computational integrity*). While most approaches "compile" each program into its fixed protocol (with a prover part and a verifier part), Cairo is a single protocol that works for any program (of some bounded size of course). They call this the CPU approach, as opposed to the ASIC approach. Effectively, the program you want to prove is encoded in some Cairo instruction set and passed as input to another program that will simply run it, like a VM. Translated in ZKP-lingo, a circuit will constrain the execution trace to match the execution of the program passed as public input. (This last sentence might be hard to understand if you are not familiar with at least one GP-ZKP system.)
Cairo is also a higher-level language, that you can play with on the Cairo playground. If you click on "debug" you can see the program it compiles to. Essentially a series of instructions and data, which you can think of as code and data segments of a binary. The rest of the memory essentially acts as a "stack" that is used during the execution of the program.
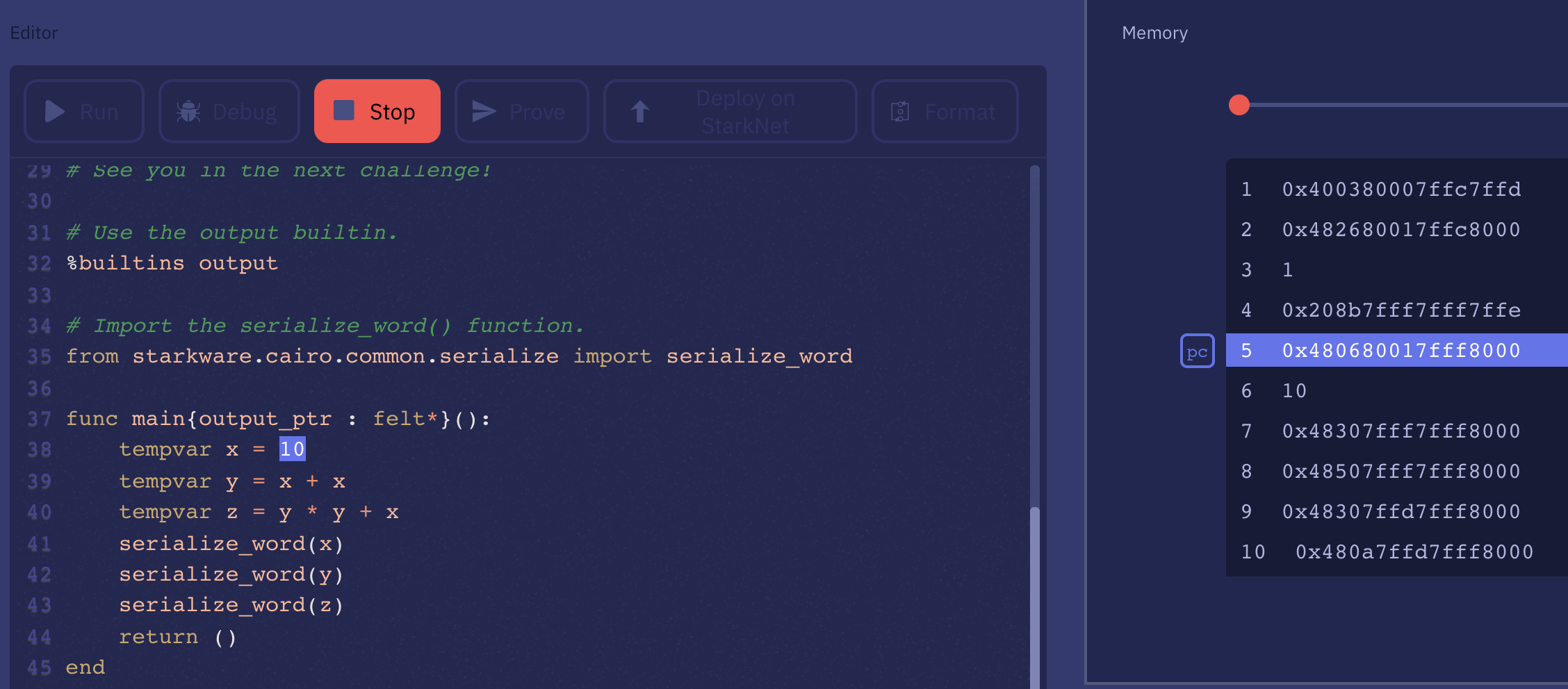
The higher-level language is out of scope of the paper. Instead, the paper details the set of instructions and its encoding, which is then unpacked in the constraint of the circuit executing the program. In the paper, they go through a simple example, the Fibonacci sequence, to illustrate how a program works and how the state transition logic works. As I had to reverse engineer it I thought I would share this here.

Here's our program, which is two instructions followed by three values.
Let's start simple and let's look at what the first instruction tells us.
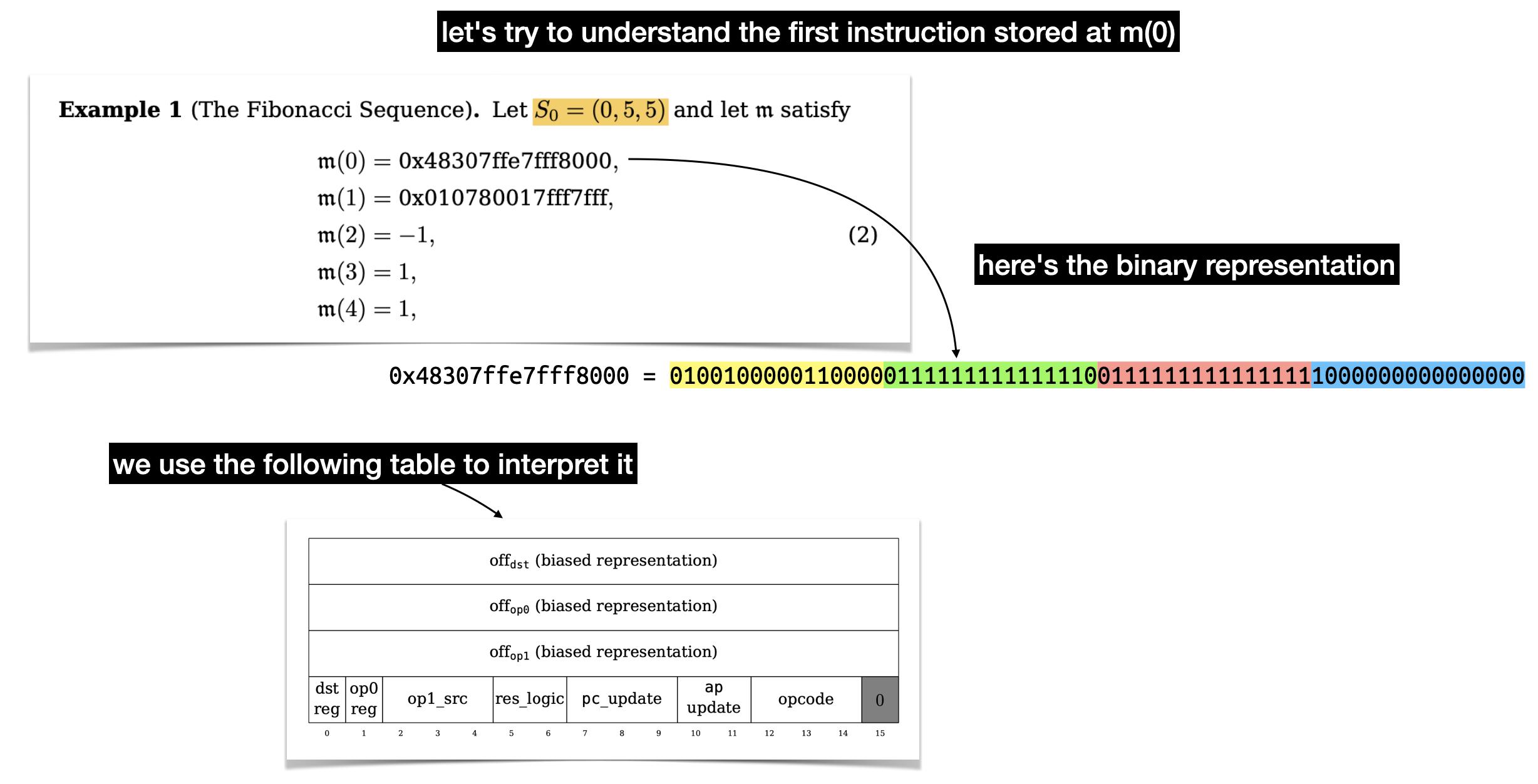
There's a lot to unpack here, there's three values of 16 bits that represent offsets in our memory. Two for the two operands (op0 and op1) of a binary operation, and one (dst) to indicate where to store the result of the operation. Let's ignore these for now and focus on the last part: the flags.
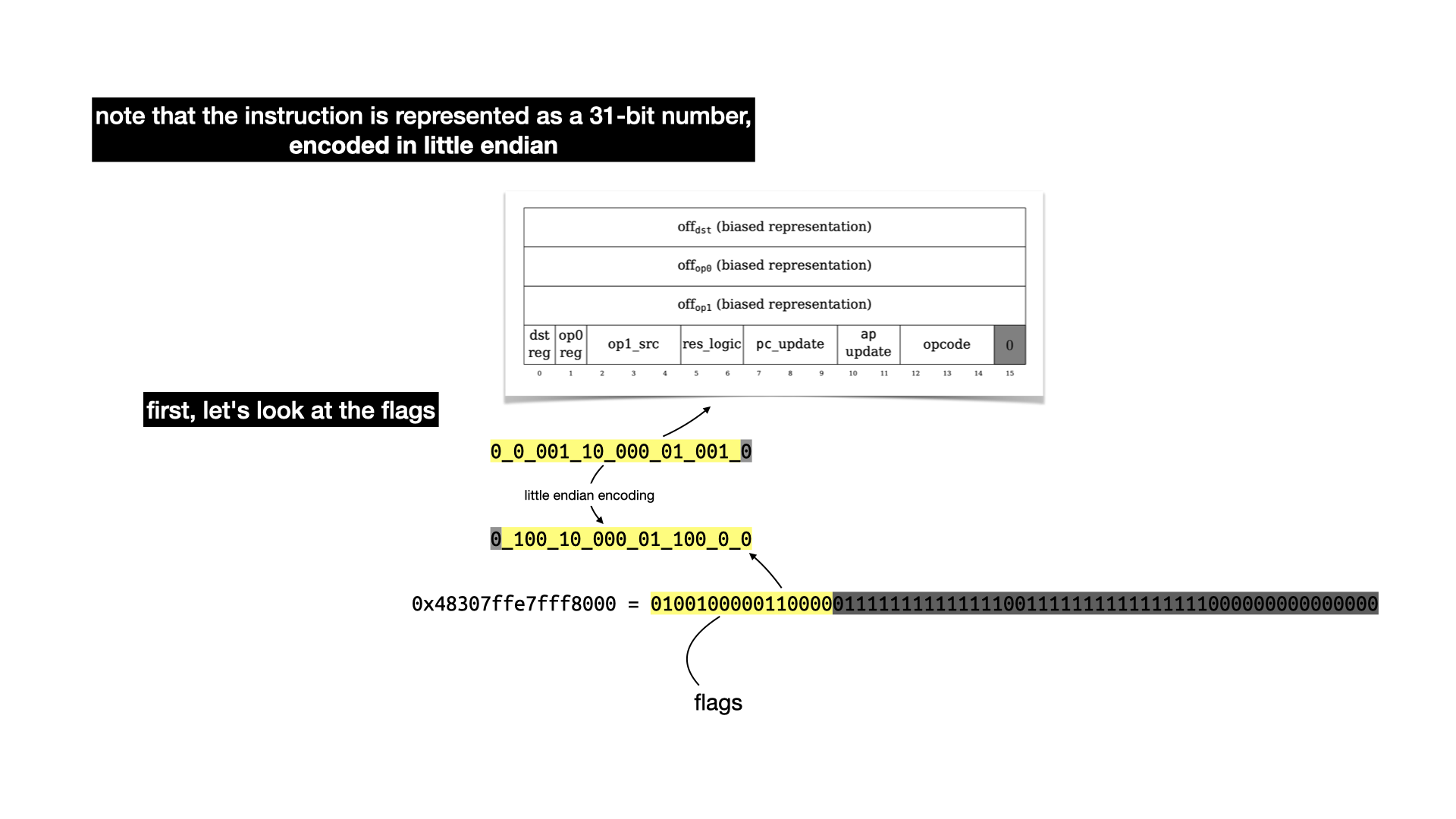
To understand what each flags do, you have to take a look at the state transition function. It's a bit confusing to follow, but there's apparently a Lean proof that it is correct (this field really keeps on giving).

A lot of this is not going to make sense without reading the paper. But there's three registers:
pc is the program counter, it points to an address in memory from where to fetch the next instruction.ap is the allocation pointer, it points to a free address in memory, useful to store data globally.fp is the frame pointer, used to store data as well when doing function calls.
The logic can be summarized as: fetch data from memory; operate on it (addition or multiplication); update the registers.
So what happens with our example's first instruction?
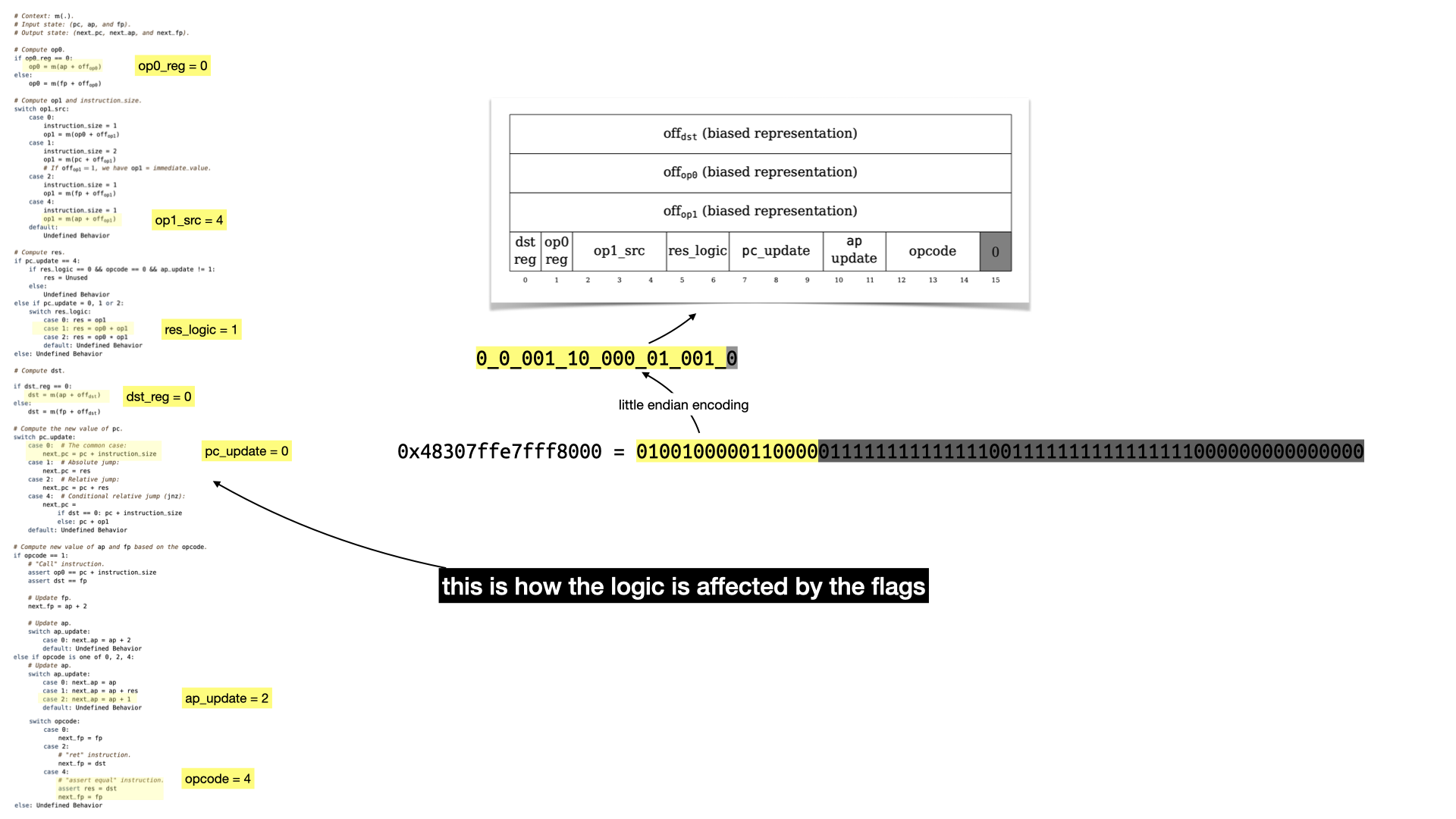
Still a bit abstract but that should give you an idea.
Before I reveal the result of the whole instruction let's look at the rest of the instruction: the offsets

The offset leaks some of the logic: -1 and -2 are the indices in the Fibonacci formula
$u_i = u_{i-1} + u_{u-2}$
Let's now reveal what the first instruction is really doing.
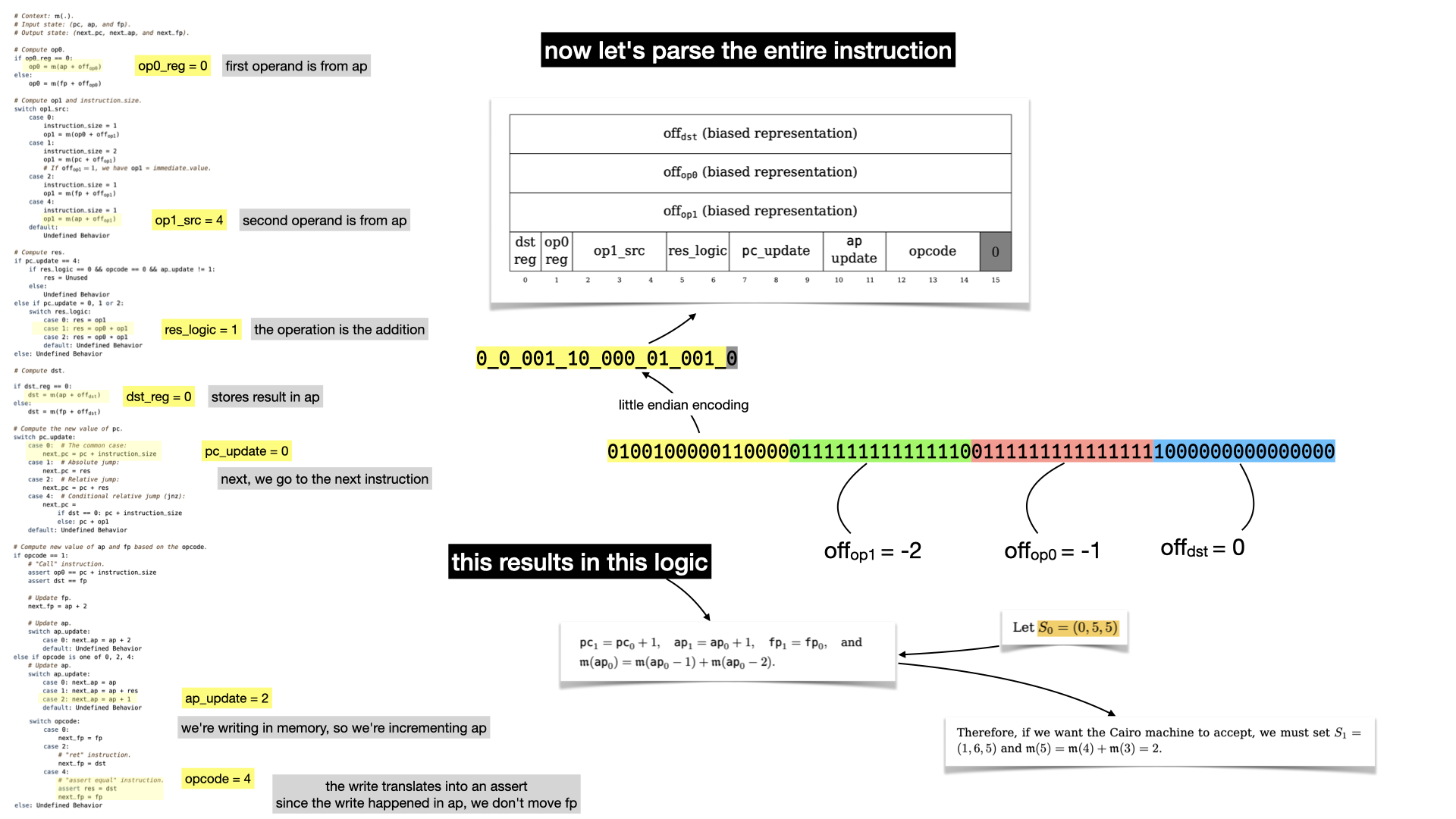
There's no doubt that if you've followed that far you must have read the paper.
What happens can be summarized as:
- we increment the program counter
pc (to go to the next instruction)
- we add the two values stored in the memory at offset
-1 and -2, and store the result in memory.
- we increment
ap, since we stored in memory. We don't touch fp since we didn't do any function call.
Let's look at the second instruction.

Let's reverse it using our table.
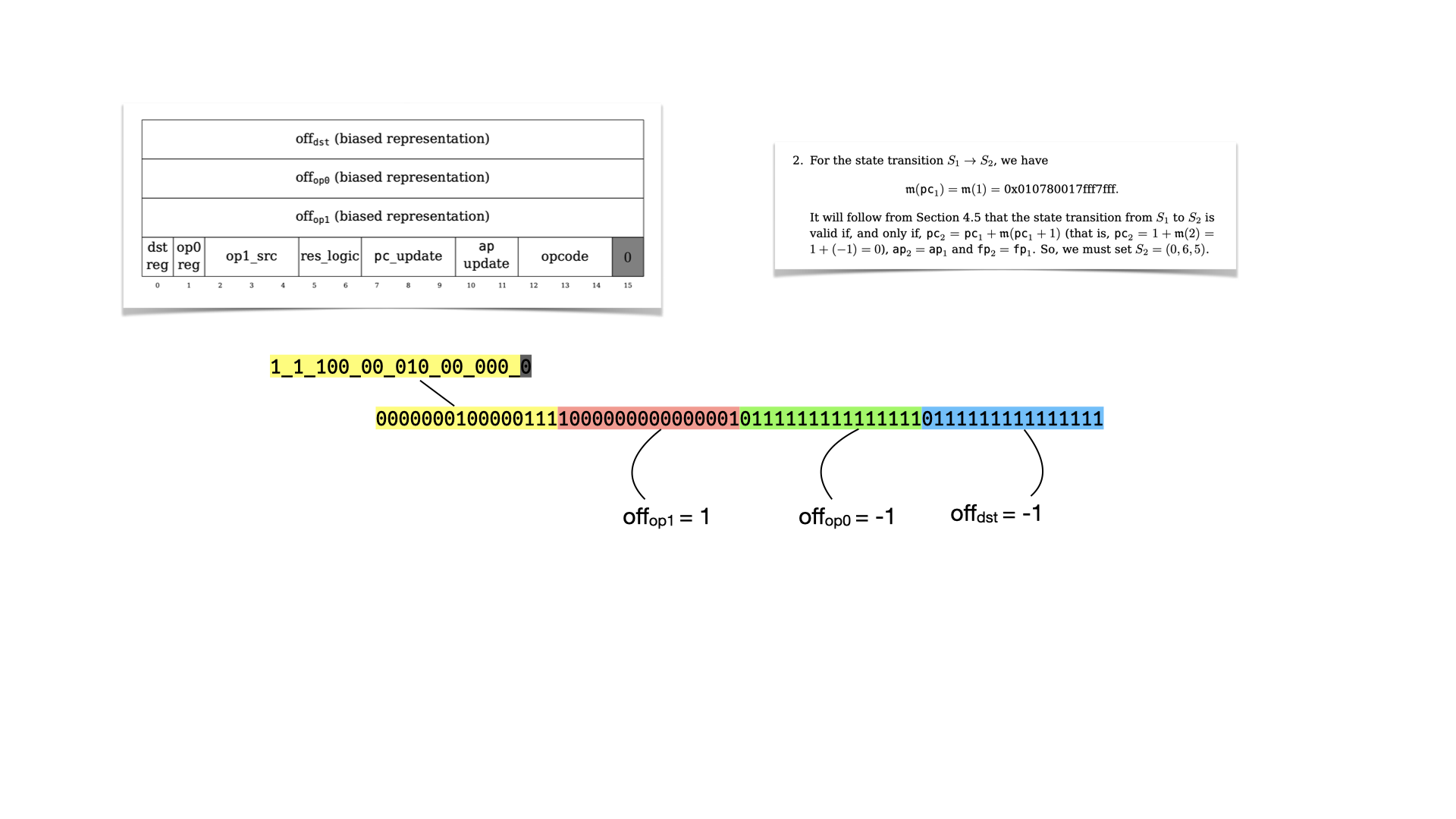
And let's look at the flags
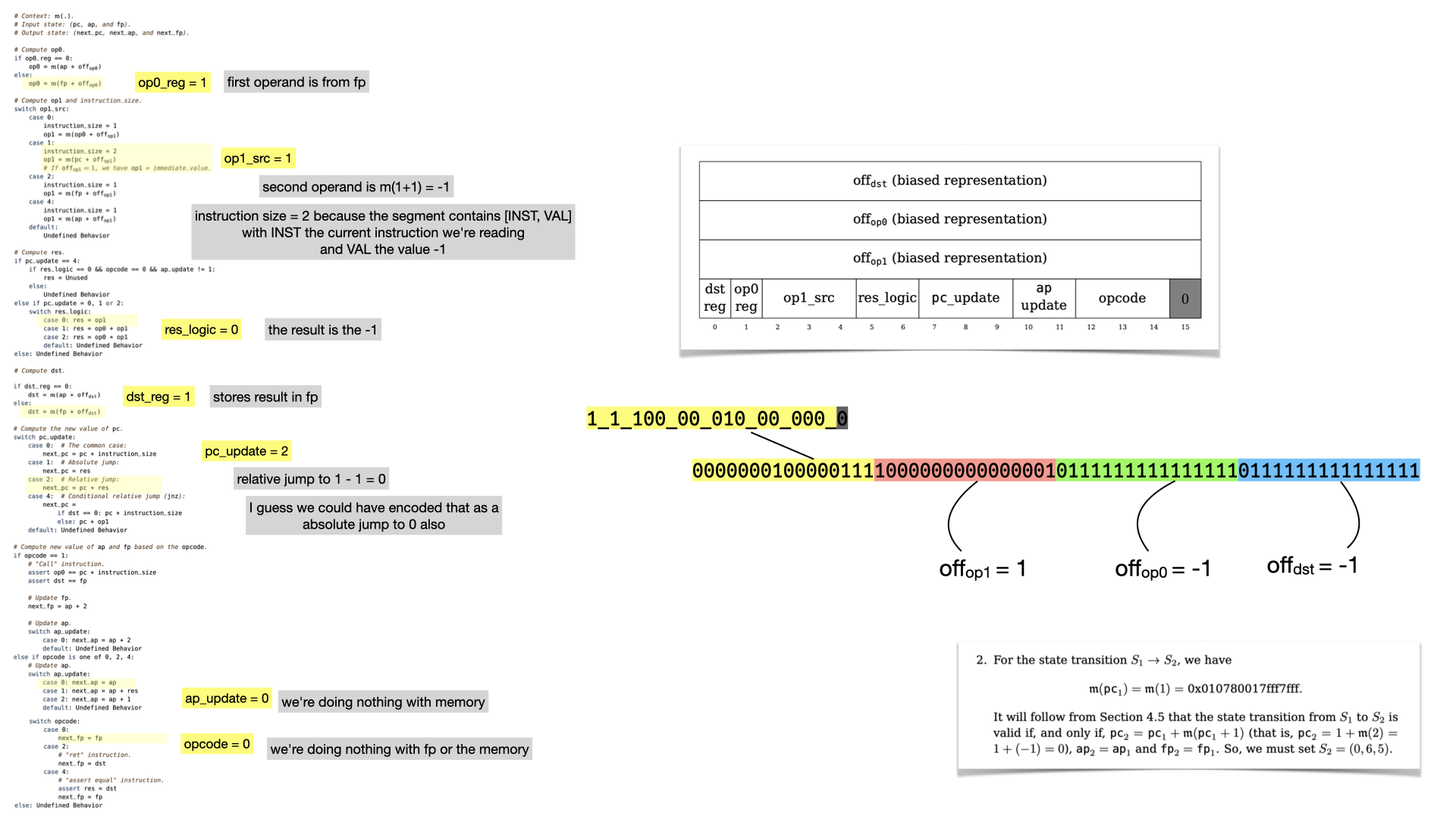
What's interesting here, is that the instruction leads to a jump! The next register values will lead to the circuit re-starting from instruction at memory address 0, because pc points to it. Thus, we're in an infinite loop, which is parameterized by the number of instructions that the prover wants to run.

I got interviewed by Quartz for their Listen to the crypto converts article.
Wong is a cryptography engineer at software development company O(1) Labs, working on the Mina cryptocurrency. He writes about crypto and cryptography at his blog, cryptologie.net, and was previously the security lead for Facebook’s Diem.
read the full interview here
I've been reading a lot of negative discussions around cryptocurrencies on some of the communities that I frequent (e.g. hackernews) and I felt the urge to write something about it.
I personally find cryptocurrencies to be an extremely interesting field of innovation because it tightly involves three interesting domains:
- The field of cryptography
- The field of economics
- The current payment system and the financial world
Lacking knowledge in any of these fields makes it extremely hard to have a good understanding of the added value of cryptocurrencies. Money is quite an abstract subject (what's a derivative? what's a CDO? what's a margin call? etc.) and it can take decades to understand how a new technology can impact money and society in general. In this post, I give my own opinion of what problems cryptocurrencies can address, while warning readers that I'm mostly involved in the field of cryptography, know a bit about the financial world, and know very little about economics. So take this post with the usual grain of salt.
The point where Blockchain became mainstream
Years ago, I was waiting in line on a beach in Chicago. I had been standing there for hours to try the HTC Vive, a virtual reality headset. What was waiting for me at the end of the line was the future, I believed it before I tried it, and I understood it after experiencing it. Yet, I managed to miss another hint of the coming times, a change that was unraveling in plain sight, invisible to my oblivious eyes.
In line, I started chatting with some older chap who got really enthusiastic when I mentioned that I was working in cryptography.
"So what do you think about the blockchain?"
I had known Bitcoin for a while at that time, but this was the first someone that appeared non-technical talked about a cryptographic term directly.
"You mean Bitcoin?"
"Yeah"
"Ah, well, I'm not sure, what else is there than the cryptocurrency itself?"
The dude then started asking me questions about where I thought the "technology" would go and how revolutionary I thought it was. Odd, I remember thinking. I couldn't see why that person was so hyped and I dismissed it as misdirected enthusiasm, thinking that there was really nothing more to Bitcoin than Bitcoin.
It's comical, in retrospect, that I failed hard to foresee the boom of the cryptocurrencies. I had invested some, and lost some during the first mtgox crash), I had even made a presentation to my classmates a few years ago as I was doing a masters on cryptography. I had found the idea really cool, perhaps it was one of the reason I ended up studying cryptography? But still, why would anyone see something more than the initial Bitcoin paper?
For many years I continued to ignore cryptocurrencies. I didn't get why more and more people would get excited. I even created some passive aggressive page, annoyed by the new use of the term "crypto" (http://cryptoisnotcryptocurrency.com).
In 2017, everything changed. At the time, I was working as a security consultant at the Cryptography Services department of NCC Group, and suddenly my team started getting more and more cryptocurrency-related work. And in turn, I got more and more interested and involved in the world of cryptocurrencies, creating the Decentralized Application Security Project Top 10 and participating in the audits of cryptocurrencies like NuCypher, Ethereum, and ZCash. The next thing I know I was leading security for the Diem cryptocurrency (formerly known as Libra) working at Novi (Facebook), two years later I was joining the cryptography team of O(1) Labs to work on the Mina cryptocurrency, and a few month ago publishing Real-World Cryptography, the first cryptography book with a chapter on cryptocurrencies.
The state of banking today
Cryptocurrencies are about the movement of money, and as such it is important to study the current ways and limitations of moving money. Without this context, cryptocurrencies do not make any sense.
Today, payment works something like this: for your bank to reach someone else's bank (your friend, your landlord, or a souvenir shop in Thailand) it needs to travel through several banks and systems. In practice, not all banks have partnerships with one another, and so your bank will have to find a route to take to reach the other bank. Different destinations mean different routes.
Banks allow movement of money by creating partnerships with other banks. It usually works like this: bank A has an account at bank B, and bank B has an account at bank A. We call that correspondent banking. If bank A wants to send some money to bank B, they'll either credit bank B's account, or bank B will debit bank A's account. (The direction might be decided on how much bank A trusts B, and vice versa.)
Of course, not all banks have partnerships, but following the six degrees of separation concept, there'll usually be a chain of banks that connect your bank from your recipient's bank.
If you're sending money within the same country, and depending on the country you're living in, you might have access to a government-operated bank that will attempt to partner with most of the territory's banks. A so-called central bank. In the US it's the Federal Reserve System (or the Fed), in France it's Banque de France, etc. Central banks have central banks too, for example, the Bank for International Settlements (BIS).
Now, let's talk speed: some of these central banks sometimes have real-time settlement systems, where money can be transferred from one bank to the other almost instantaneously. These are usually called real-time gross settlements (RTGSs), where "gross" means that you're not batching several transactions together. Most banks, as I understand, use deferred net settlements to batch transactions: once (or sometimes several times) a day money moves from one bank to another bank.
Thus, to transfer money from your bank to a recipient's bank, your money has to go through a chain of bank accounts. Some of these movements will be settled instantly, some of these movements will be settled after hours or days. This is why payments can be slow depending on the route your money takes.
Money is (badly) decentralized
If you dig deeper, you realize that different banks use different protocols, these protocols are old, badly designed, and errors happen constantly. The only way to make sure that money is not created out of thin air (double spending) is to constantly perform manual audits: having actual humans read balance sheets.
One of my friend working at a European bank described to me one of the many incidents they had. To settle with some other bank, they use some XML protocol to communicate how much Euro should move between the banks, and that twice a day. Usually, there's always money moving. Yet, one day, the correspondent bank did not send them any second transfer before the end of the day. My friend's bank took this as a "let's replay the previous settlement" and started crediting thousands of clients with sums of money they had already received. Employees had to work nights to revert everything and make sure that money was not lost. Imagine that.
And that's just one bank, every bank is doing their own thing to an extent. There are some standardization effort, as there usually is when things get bad, but they move slowly. It also doesn't fix the elephant in the room: money is too heavily and badly decentralized, and every bank is on a quest to partner with every other bank, creating an $O(n^2)$ nightmare.
All the solutions that attempt at fixing the system are pretty much trying to centralize more of the system. The fastest points of payments are central banks and other single points of failure like Wise. One interesting development is that some of these central banks are realizing that they need to support instant payments, better security, good interoperability, and perhaps all of that even for people like you and I (the retail). This is what you might have heard as central bank digital currencies (CBDCs).
This reduces the $O(n^2)$ issue, but it also introduces another one: the issue of trust. Why would central banks trust one another? The more you centralize, the more trust you need to have in that single point of failure.
This is the big innovation behind cryptocurrencies: they seek to centralize the financial backbone to facilitate the movement of money. That is, cryptocurrencies are distributed systems, which ultimate goal is to simulate centralized systems while removing single points of failure. In such systems, users all connect to what appears to be, and work like, a single server. No need to connect users between them, in the peer-to-peer way I described previously, now the simulated single machine is connecting everyone together. Money takes the shortest route possible.
In some sense, a cryptocurrency is like a central bank that anyone can connect to and that processes transfer in real time, but internally it has no single points of failure, provides insurance based on cryptography, and offers transparency to external users.
A tiny introduction to the fundamentals
Don't run away. I promise this is a tiny, brief, understandable, introduction to the fundamentals of cryptocurrencies.
Imagine that a hundred participants decide to create this centralized bank. To do that, they all decide to start from the same ledger, a book of all account balances (and transactions). The first page (or block) might read:
Bob has 3 tokens, Alice has 2 tokens
This is the genesis, in crypto term. Once each participant has retrieved their copy of the ledger, they need to figure out a way to agree on who gets to add new pages in the book. For example, adding a page could look like:
Alice sends 2 tokens to Charles; Bob sends 1 token to Alice
And as they add pages, they also need to make absolutely sure that they are all adding the same pages. If a participant adds a different page than everyone else, we have what we call a fork. That participant would start living in a different world.
A very simple way to decide on who gets to add pages to the ledger, is to do a round robin: I go first, then you, then him, then her, then me again, then you, etc. That works well if the set of participants is known and fixed (which is what Libra/Diem does, and it's called proof of authority).
Other cryptocurrencies might want to dynamically choose who gets to be the next leader based on how much tokens they have (this is called proof of stake, like Tendermint).
Now, Bitcoin did things differently, it let everybody have a chance at choosing the next page! To participate, you play a lottery with your computer and if you get the winning ticket you get to decide on the next set of transactions (the next block). This was called proof of work, and as you probably know it, the lottery is computationally expensive to play. Due to that, today, most modern cryptocurrencies use a proof of stake approach.
Last Tuesday was the start of ZK HACK, a "7-week virtual event featuring weekly workshops and advanced puzzle solving competitions". All related to zero-knowledge proofs, as the name suggests. The talks of the first day were really good, and you can rewatch them here. At the end of the first day, a puzzle called Let's hash it out was released. This post about solving this puzzle.
The puzzle
The puzzle is a Github repo containing a Rust program. If you run it, it displays the following message:
Alice designed an authentication system in which users gain access by presenting it a signature on a username, which Alice provided.
One day, Alice discovered 256 of these signatures were leaked publicly, but the secret key wasn't. Phew.
The next day, she found out someone accessed her system with a username she doesn't know! This shouldn't be possible due to existential unforgeability, as she never signed such a message.
Can you find out how it happend and produce a signature on your username?
Looking at the code, it looks like there's indeed 256 signatures over 256 messages (that are just hexadecimal strings though, not usernames).
The signature verification
The signatures are BLS signatures (a signature scheme that makes use of pairing and that I've talked about it here).
Looking at the code, there's nothing fancy in there. There's a verification function:
pub fn verify(pk: G2Affine, msg: &[u8], sig: G1Affine) {
let (_, h) = hash_to_curve(msg);
assert!(Bls12_381::product_of_pairings(&[
(
sig.into(),
G2Affine::prime_subgroup_generator().neg().into()
),
(h.into(), pk.into()),
])
.is_one());
}
which pretty much implements the BLS signature verification algorithm to check that
$$
e(\text{sig}, -G_2) \cdot e(\text{h}, \text{pk}) = 1
$$
Note: if you read one of the linked resource, "BLS for the rest of us", this should make sense. If anything is confusing in this section, spend a bit of time reading that article.
We know that the signature is simply the secret key $sk$ multiplied with the message:
$$\text{sig} = [\text{sk}]h$$
The public key is simply the secret key $\text{sk}$ hidden in the second group:
$$\text{pk} = [\text{sk}]G_2$$
So the check gives us:
$$
\begin{align}
& \;e([sk]h, -G_2) \cdot e(h, [sk]G2) \
=& \;e(h, G_2)^{-\text{sk}} \cdot e(h, G_2)^\text{sk} \
=& \;1
\end{align}
$$
The hash to curve
Actually, the username is not signed directly. Since a signature is the first argument in the pairing it needs to be an element of the first group (so $[k]G_1$ for some value $k$).
To transform some bytes into a field element $k$, we use what's called a hash-to-curve algorithm. Here's what the code implements:
pub fn hash_to_curve(msg: &[u8]) -> (Vec<u8>, G1Affine) {
let rng_pedersen = &mut ChaCha20Rng::from_seed([
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1,
]);
let parameters = CRH::<G1Projective, ZkHackPedersenWindow>::setup(rng_pedersen).unwrap();
let b2hash = blake2s_simd::blake2s(msg);
(
b2hash.as_bytes().to_vec(),
CRH::<G1Projective, ZkHackPedersenWindow>::evaluate(¶meters, b2hash.as_bytes())
.unwrap(),
)
}
What I'm reading is that it:
- initializes some collision-resistant hash function (CRH) from a hardcoded seed
- uses the BLAKE2 hash function to hash the username (
msg) into 256 bits.
- Uses the CRH to hash the BLAKE2 digest into a group element
Looking at CRH, it's simply a Pedersen hashing (I've talked about that hash function here) that converts a series of bits $b_1, b_2, b_3, \cdots$ into
$$
[b_1]G_{1,1} + [b_2]G_{1, 2} + [b_3]G_{1, 3} + \cdots
$$
where the $G_{1,i}$ are curve points that belongs to the first group (generated by $G_1$) and derived randomly via the hardcoded seed (in a way that prevents anyone from guessing their discrete logarithm).
What are we doing?
What are we looking for? We're trying to create a valid signature (maybe a signature forgery attack then?) on our own nickname (so more than just an existantial forgery, a chosen-message attack).
We can't change the public key (so no rogue key attack), and the message is fixed. This leaves us with the signature as the only thing that can be changed. So indeed, a signature forgery attack.
To recap, we have 256 valid signatures:
- $e(\text{sig}_1, -G_2) \cdot e(h(m_1), \text{pk}) = 1$
- $\vdots$
- $e(\text{sig}_{256}, -G_2) \cdot e(h(m_{256}), \text{pk}) = 1$
and we want to forge a new one such that:
$$
e(\text{bad_sig}, -G_2) \cdot e(h(\text{"my nickname"}), \text{pk}) = 1
$$
Forging a signature
Reading on the aggregation capabilities of BLS, it seems like the whole point of that signature scheme is that we can just add things with one another. So let's try to think about adding signatures shall we?
What happens if I add two signatures?
$$
\begin{align}
&\; \text{sig}_1 + \text{sig}_2 \
=&\; [\text{sk}]h_1 + [\text{sk}]h_2
\end{align}
$$
if only we could factor $sk$ out... but wait, we know that $h_1$ and $h_2$ are additions of the same curve points (by definition of the Pedersen hashing):
$$
\begin{align}
&\; \text{sig}_1 + \text{sig}_2 \
=&\; [\text{sk}]h_1 + [\text{sk}]h_2 \
=&\; \text{sk}\
&\; + \text{sk}
\end{align}
$$
where the $b_{i}$ (resp. $b'_{i}$) are the bits of $h_1$ (resp. $h_2$). So the added signature are equal to the signature of the added bitstrings:
$$
[b_{1} + b'{1},\; b{2} + b'{2},\; b{3} + b'_{3},\; \cdots]
$$
We just forged a signature! Now, that shouldn't mean much, because remember, these bits represent the output of a hash function and a hash function is resistant against pre-image attacks.
Wait a minute...
Our hash function is a collision-resistant hash function, but that's it.
Linear combinations
OK, so we forged a signature by adding two signatures. But we probably didn't get what we wanted, what we wanted is to obtain the bits $\tilde{b}_1, \tilde{b}_2, \tilde{b}_3, \cdots$ that represent the hashing of my own username.
Maybe if we add more signatures together we can get? Actually, we can use all the signatures and combine them. And not just by adding them, we can take any linear combination (we're in a field, not constrained by 0 and 1).
So here's the system of equations that we have to solve:
- $\tilde{b}_1 = x_1 b_1 + x_2 b'_1 + x_3 b''_1$
- $\vdots$
- $\tilde{b}_{256} = x_1 b_{256} + x_2 b'_{256} + x_3 b''_{256}$
Note that we can see that as solving $xA = b$ where each row of the matrix $A$ represents the bits of a digest, and $b$ is the bitvector of my digest (the hash of my username).
Once we find that linear combinations, we just have to apply it to the signatures to obtain a signature that should work on my username :)
$$
\text{bad_sig} = x_1 \text{sig}_1 + x_2 \text{sig}_2 + x_3 \text{sig}_3 + \cdots
$$
Coding the answer
Because I couldn't find a way to solve a system of equations in Rust, I simply extracted what I needed and used Sage to do the complicated parts. Here's the Rust code that creates the matrix $A$ and the vector $b$:
// get puzzle data
let (_pk, ms, _sigs) = puzzle_data();
// here's my name pedersen hashed
let (digest_hash, _digest_point) = hash_to_curve("mimoo".as_bytes());
// what's that in terms of bits?
use ark_crypto_primitives::crh::pedersen::bytes_to_bits;
let bits = bytes_to_bits(&digest_hash);
let bits: Vec<u8> = bits.into_iter().map(|b| b as u8).collect();
// order of the subgroup of G1
println!("R = GF(0x73eda753299d7d483339d80809a1d80553bda402fffe5bfeffffffff00000001)");
// xA = b
print!("A = matrix(R, [");
for m in ms {
let (digest, _point) = hash_to_curve(&m);
let bits = bytes_to_bits(&digest);
let bits: Vec<u8> = bits.into_iter().map(|x| x as u8).collect();
print!("{:?}, ", bits);
}
println!("b = vector(R, {:?})", bits);
Note: the system of equation is over some field $R$. Why? Because eventually, the linear combination happens between curve points that are elements of the first group, generated by $G_1$, and as such are scalars that live in the field created by the order of the group generated by $G_1$.
In sage, I simply have to write the following:
x = A.solve_left(b)
and back in Rust we can use these coefficients to add the different signatures with one another:
let mut bad_sig = G1Projective::zero();
for (coeff, sig) in coeffs.into_iter().zip(sigs) {
let coeff = string_int_to_field_el(coeff);
bad_sig += sig.mul(coeff);
}
// the solution
verify(pk, "mimoo".as_bytes(), bad_sig.into());
It works!
Don't worry about the pretentious title, I was just inspired by Rob Pike's 5 Rules of Programming and by the Risk Manifesto of the The Security Engineer Handbook (which is explained in more details in the book):
Threat modeling over mindless improvements.
Secure early rather than later.
Forcing software over forcing people.
Role play over complacency.
So I made my own! Without further ado:
- Put it in writing. If you leave for a month-long spiritual trip and someone needs to fix a bug in your code, will they have to wait for you? If an expert wants to assess the algorithm you're implementing, but have no knowledge in the programming language you used, will they manage to do it? These are questions you should ask yourself when writing a complex piece of code. It happens often enough that a protocol is implemented differently from the paper. Write specifications!
- The concorde is fast but dangerous. When writing optimized, faster code, or perhaps over-engineered or overly-clever code, you're trading off maintainability, clarity, and thus security of your code. I often hear programming language features claiming zero-overhead, but they always forget to talk about the cost paid in ambiguity and complexity.
- Plant types and data structures, then water. As Rob Pike says, use the right data structures, from there everything should flow naturally. Well documented structures are the best abstraction you'll find. Furthermore, functions that make too many assumptions on their inputs will have trouble down the line when someone changes the code underneath them. Encoding invariants in your types is a great way to address this issue. The bottom line is that you can get most of your clarity and security through creating the right types and objects!
- Don't let your dependencies grow on you. Dependencies easily grow like cancer cells. Beware of them. Analyse your dependencies, monitor and review the ones you use, rewrite or copy code to avoid importing large dependencies, and add friction to your process of adding new dependencies. Supply-chain attacks are being more and more of a thing, be aware.
- Make the robots enforce it. Enforce good code patterns and prevent bad code patterns through continuous integration where you can. This is pretty much to the "forcing software over forcing people" of the Risk Manifesto.
- Design lego cities, not real ones. The less connected your code is, the clearer it is to follow as the different parts will be self-contained, and the easier it will be to update some part of the code. Think about parts of your code as external libraries that are facing more than just your codebase.
Believe it or not, even though I was one of the participant in the standardization of ERC-721, the Ethereum standard for NFTs, I had never read the final standard, yet alone written an ERC-721 smart contract. At the time I was against the standard, at least in its form, due to its collision with the ERC-20 standard (you can't create a smart contract that is both a compliant ERC-20 token and a compliant ERC-721 NFT). My arguments ended up losing, ERC-721 was standardized with the same function names as ERC-20, and I heard that today another standard is surfacing (ERC 1155) to fix this flaw (among others).
Anyway, I recently decided to bury the hatchet and read the damn standard. And after a few weekends of hacking with my friends Eric Khun and Simon Patole, we wrote an ERC-721 compliant dapp as an art project. It's called project memento and it boasts a grid of tiles each containing a letter, a-la million dollar page. People can acquire letters, alter them, and form lines (or diagonals) of words together. I'm curious as to what will become of this, but this was fun!

You can check out project memento here
Today I received the first copy of my book Real-World Cryptography! You can't imagine how much sweat and love I put into this work in the last two years and a half. It's the book I've always wanted to read, and it's the book I thought the field was missing. It's the book I wanted to have as a student when I was learning about hash functions and ciphers, and it's the book I wish I could have referred to my fellow pentesters when they had questions about TLS or end-to-end encryption. It's the book I'd use as a developer looking for cryptographic libraries and best practice. It's the first book with a cryptocurrency chapter, and it's the book cryptographers will read to learn about password-authenticated key exchanges, sponge functions, the noise protocol framework, post-quantum cryptography, and zero-knowledge proofs. Real-world cryptography is what the field of applied cryptography really looks like today. It's all there.
Get the book here!






Hey you!
If you've been following my blog recently, you must have seen that I joined O(1) Labs to work on the Mina cryptocurrency. Why? Simply because I felt like it was the most interesting project in the space, and now that I'm deep in OCaml and Rust code trying to understand PLONK and other state-of-the-art zero-knowledge proof systems work I can tell you that it is indeed the most interesting project in the space :)
My two zero-knowledge friends are too busy doing a PhD. They like self-inflicted pain. (Mathias and Michael, I'm looking at you.) So if you're free, ping me! And if you're not free, ping me anyway because we might be able to work something out.
Because people need a job description, check that one out: https://boards.greenhouse.io/o1labs/jobs/4023646004
But realistically, just contact me on twitter or here if you have any question about what the culture of the company is, what your day-to-day would look like, and if you can work remotely (yes).




















