Let's Encrypt Overview posted June 2015

What is Let's Encrypt?

Basically, it's a way to get a quick x509 certificate for your server without knowing much about what is a x509 certificate:

You have a website. You want people to be able to log in on it from starbucks without the guy sitting at a near table reading the passwords in clear from the packets you're sending everyone around you. So you google a few random keywords like "secure website https" and you end up with a bunch of links and services (which may not be free) and you suddenly have to understand what are certificates, PKI, x509, public-key cryptography, RSA, FQDN, haaa.... Well, worry no more, Let's Encrypt was thought so that you wouldn't have to go through all that trouble and destroy your server on the way.

Oh and yeah. It's for free. But is hasn't been released yet.

How does it work?

You can learn more reading their technical overview, or some of their videos... or read my tl;dr:

1. You download their program on your server that has the address www.example.com:

sudo apt-get install lets-encrypt

1. You run it as sudo telling it you want to get a certificate for your domain

lets-encrypt example.com

And voila.

Behing the curtains this is what happens:

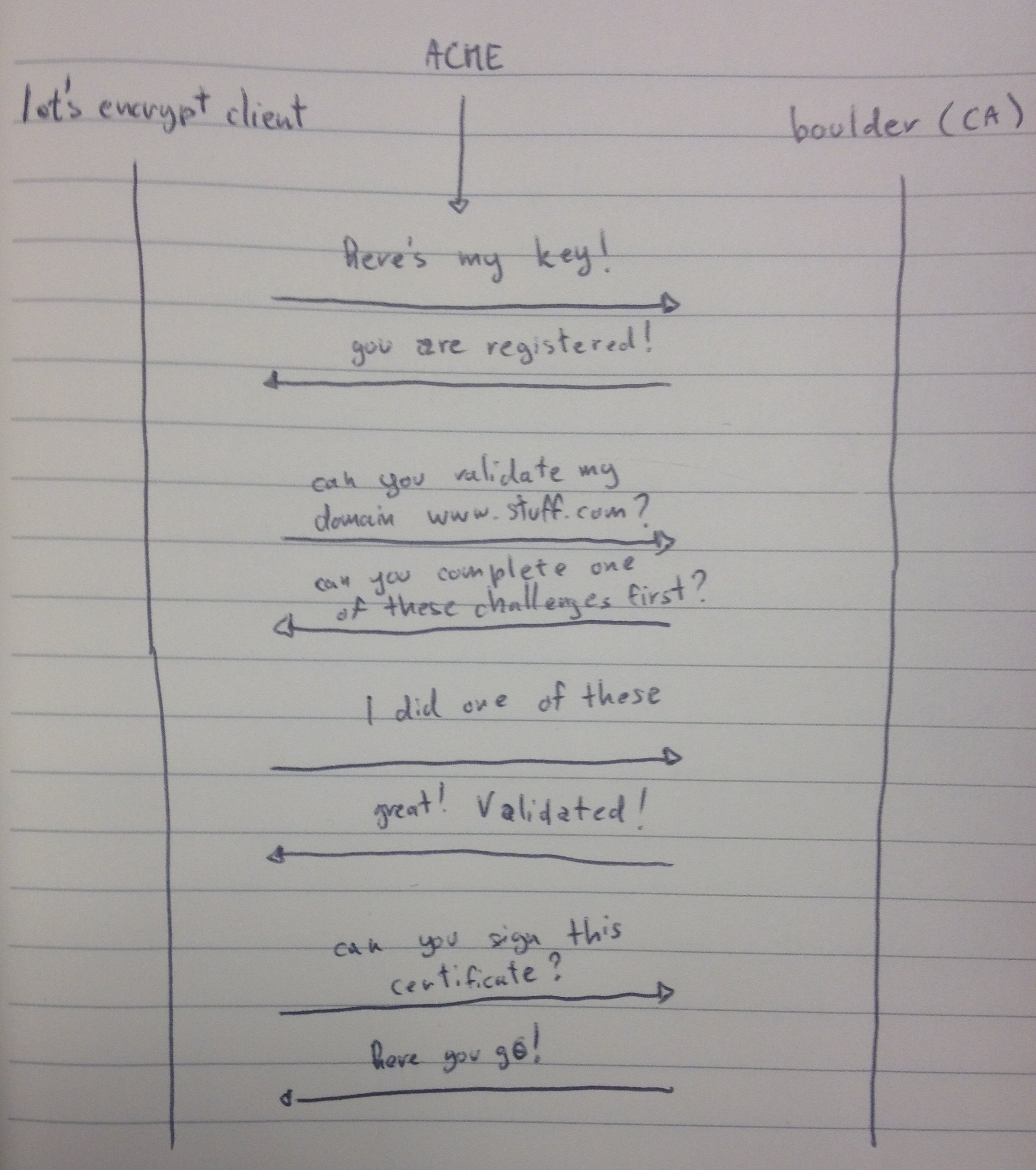
1. lets-encrypt will generate a pair of RSA private key/public key and contact the CA with your public key.

2. The CA will register your public key

3. The program will then ask the CA to verify your domain.

4. The CA will answer with a set of challenges. These are some tasks you can complete to prove to the CA you own that domain. One of the common one is to upload a certain file at a certain address of that domain.

5. The program you installed will then do that for you and poll the CA for a confirmation

6. The CA will tell you "OK man, all is good".

7. The program will then generate another long term pair of private key/public key, generate a CSR (Certificate Signing Request) with the new public key and send that CSR to the CA.

8. The CA will extract the information, create a beautiful x509 certificate, sign it and send it back to you.

9. lets-encrypt will install the certificate on your server and set certain options (or not) to force https

By the way, the certificate you will get will be a DV certificate, meaning that they only verified that you owned the domain, nothing more. If you want an EV certificate this is what you will have to go through (according to wikipedia):

• Establish the legal identity as well as the operational and physical presence of website owner;
• Establish that the applicant is the domain name owner or has exclusive control over the domain name; and
• Confirm the identity and authority of the individuals acting for the website owner, and that documents pertaining to legal obligations are signed by an authorised officer.

But how does it really work?

So! The lets-encrypt program you run on your server is open sourced here: https://github.com/letsencrypt/lets-encrypt-preview. It is called lets-encrypt-preview I guess because it isn't done yet. It's written in Python and has to be run in sudo so that it can do most of the work for you. Note that it will install the certificates on your server only if you are using Apache or Nginx. Also, the address of the CA is hardcoded in the program so be sure to use the official lets-encrypt.

The program installed on the CA is also open sourced! So that anyone can publicly review and audit the code. It's called Boulder and it's here: https://github.com/letsencrypt/boulder and written in Go.

Lets-encrypt and Boulder both use the protocol ACME for Automated Certificate Management Environment specified here as a draft: https://letsencrypt.github.io/acme-spec/

ACME

ACME is written like a RFC. It actually wants to become an RFC eventually! So if you've read RFCs before you should feel like home.

The whole protocol is happening over TLS. As a result the exchanges are encrypted, you know that you are talking to the CA you want to talk to (eventhough you might not use DNSSEC) and replay attacks should be avoided.

The whole thing is actually a RESTful API. The client, you, can do GET or POST queries to certains URI on the CA webserver.

Registration

The first thing you want to do is register. Registration is actually done by generating a new pair of RSA keys and sending them the public key (along with your info).

ACME specifies that you should use JWS for the transport of data. Json Web Signature. It's basically Json with authentication (so that you can sign your messages). It actually uses a variant of JWS called Jose that doesn't use a normal base64 encoding but that's all you should know for now. If you really want to know more there is an RFC for it.

So here what a request should look like with JWS (your information are sent unencrypted in the payload field (but don't worry, everything is encrypted anyway because the exchange happens over TLS)):

POST /acme/new-registration HTTP/1.1
Host: example.com

{
 "payload":"<payload contents>",
 "signatures":[
  {"protected":"<integrity-protected header 1 contents>",
   "header":<non-integrity-protected header 1 contents>,
   "signature":"<signature 1 contents>"}
}

Boulder will check the signature with the public key you passed, verify the information you gave and eventually add you to its database.

Once you are registered, you can perform several actions:

• Update your infos
• Get one domain authorized (well actually as many as you'd like)

The server will authenticate you because you will now send your public key along AND you will sign your requests. This all runs on top of TLS by the way. I know I already said that.

Boulder's guts

Boulder is separated in multiple components, this makes the code clearer and ensure that every piece of code does what it is supposed to do and nothing more.

One of the components is called the Web-Front-End (WFE) and is the only one accepting queries from the Client. It parses them, verifies them and passes them to the Registration Authority (RA) that combines the other authorities together to produce a response. The response is then passed back to the WFE and to the client over the ACME protocol. Are you following?

TWe'll see what other authorities the RA has access to in the next queries the client can do. But just to talk about the previous query, the new registration query, the RA talks to the Storage Authority that deals with the database (Which is currently SQLlite) to register your new account.

All the components can be run from a single machine (for the exception of the CA that runs on another library), but they can also be run seperately from different machines that will communicate on the same network via AMQP.

New Authorization

Now that you are registered, you have to validate a domain before you can request a certificate.

You make a request to a certain URI.

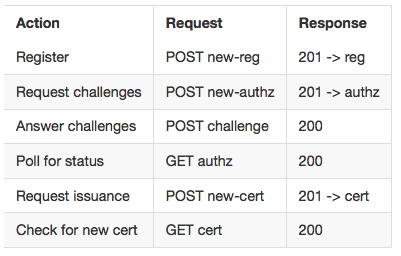
Well to be exact you make a POST request to /new-authz, and the response will be 201 if it works. It will also give you some information about where you can go next to do stuff (/authz)

Here's the current list of API calls you can do and the relevant answers.

The server will pass the info to the Policy Authority (PA) and ask it if it is willing to accept such a domain. If so, it will then answer with a list of challenges you can complete to prove you own the domain, along with combinations of accepted challenges to complete. For now they only have two challenges and you can complete either one:

• SimpleHTTPS

• DVSNI

If you choose SimpleHTTPS the lets-encrypt client will generate a random value and upload something at the address formed by a random value the CA sent you and the random value you generated.

If you choose DVSNI, the client will create a TLS certificate containing some of the info of the challenge and with the public key associated to his account.

The client then needs to query the CA again and the CA's Validation Authority (VA) will either check that the file has been uploaded or will perform a handshake with the client's server and verify that specific fields of the certificates have been correctly filled. If everything works out the VA will tell the RA that will tell the WFE that will tell you...

After that you are all good, you can now make a Certificate Signing Request :)

New Certificate

The agent will now generate a new pair of private key/public key. And create a CSR with it. So that your long term key used in your certificate is not the same as your let's encrypt account.

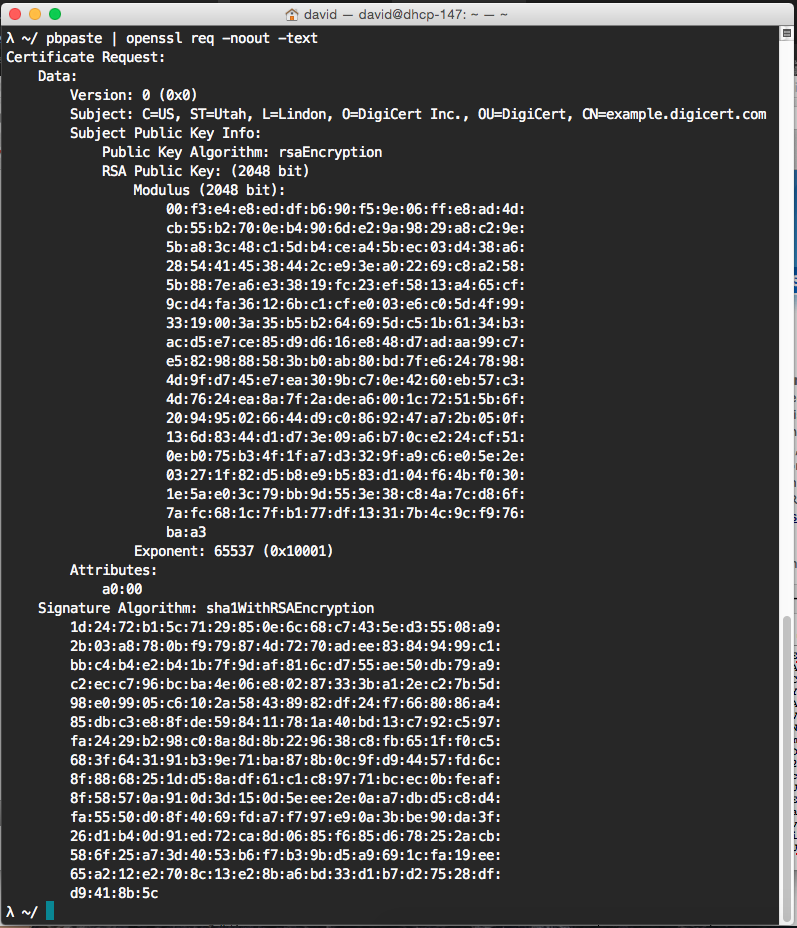
a CSR example, containing the identifier and the public key

After reception of it, the Web-Front-End of Boulder will pass it to the Registration Authority (RA) which will pass it to the Certificate Authority (CA) that will do all the work and will eventually sign it and send it back to the chain.

1: Client ---new-cert--> WFE
2:                       WFE ---NewCertificate--> RA
3:                                                RA ---IssueCertificate--> CA
4:                                                                          CA --> CFSSL
5:                                                                          CA <-- CFSSL
6:                                                RA <------return--------- CA
7:                       WFE <------return------- RA
8: Client <------------- WFE

Oh and also. the CA is talking to a CFSSL server which is CloudFlare's PKI Toolkit, a nice go library that you can use for many things and that is used here to act as the CA. CFSSL has recently pushed code to be compatible with the use of HSM which is a hardware device that you HAVE to use to sign keys when you are a CA.

After reception the lets-encrypt client will install the fresh certificate along with the chain to the root on your server and voila!

You can now revoke a certificate in the same way, but interestingly you won't need to sign the request with your account key, but with the private key associated to your certificate's public key. So that even if you lose your agent's key you can still revoke the certificate.

Other stuff

There are a bunch of stuff that you will be able to do with the lets-encrypt client but that haven't been implemented yet:

• Renew a certificate
• Read the Terms of Service
• Query OCSP requests (see if a certificate has been revoked) ...

Moar

This post is a simplification of the protocol. If you want to know more and don't want to dig in the ACME specs right now you can also take a look at Boulder's flow diagrams.

If you've followed the news you should have seen that Let's Encrypt just generated its root certificate along with several other certificates: https://letsencrypt.org/2015/06/04/isrg-ca-certs.html

This is because when you are a CA you are suppose to keep the root certificate offline. So you sign a (few) certificate(s) with that root, you lock that root and you use the signed certificate(s) to sign other certificates. This is all very serious because if something goes wrong with the root certificate, you can't revoke anything and well... the internet goes wrong as a result (until vendors start removing these from their list of trusted roots).
So the keys for the certificate have to be generated during a "ceremony" where everything is filmed and everyone must authenticate oneself at least with two different documents, etc... Check Wikipedia's page on Key Ceremony it's "interesting".

Also, I received a note from Seth David Schoen and I thought that was an interesting anecdote to share :)

the name "Boulder" is a joke from the American children's cartoon Looney Tunes:
https://en.wikipedia.org/wiki/Wile_E._Coyote_and_The_Road_Runner
This is because the protocol that Boulder implements is called ACME, which was also the name of the company that made the products unsuccessfully used by the coyote to attempt to catch the roadrunner. https://en.wikipedia.org/wiki/Acme_Corporation
Two of those products were anvils (the original name of the CA software) and boulders.

Nist ECC Workshop posted June 2015

The Nist Workshop on Elliptic Curves is live now and streaming here: http://www.nist.gov/itl/csd/ct/eccworkshop_webcast.cfm

here is the timeline: http://www.nist.gov/itl/csd/ct/ecc-workshop.cfm

Links from the past weeks posted June 2015

I've been posting some more links to the links section:

Daniel J. Bernstein: "How to manipulate standards"

DJB being DJB

Downloading Software Safely Is Nearly Impossible

The funny tale of a dude who wants to safely ssh to his server on his brand new windows laptop. This follows by how to safely download, execute and use PuttY... and it's hilarious.

About Public Key Pinning

Cloudflare explains Logjam

An awesome article written by Filippo that complements mine quite well. I don't know who made this logo but it rocks!

Recent Hacks

A timeline of famous hacks, leaks, etc... If you are curious

Cooperative Strategy

A whitehouse blogpost by Ed Felten on cooperative strategy, a nice counter-intuitive puzzle that I will not forget!

Alice and Bob are playing a game. They are teammates, so they will win or lose together. Before the game starts, they can talk to each other and agree on a strategy.
When the game starts, Alice and Bob go into separate soundproof rooms – they cannot communicate with each other in any way. They each flip a coin and note whether it came up Heads or Tails. (No funny business allowed – it has to be an honest coin flip and they have to tell the truth later about how it came out.) Now Alice writes down a guess as to the result of Bob’s coin flip; and Bob likewise writes down a guess as to Alice’s flip.
If either or both of the written-down guesses turns out to be correct, then Alice and Bob both win as a team. But if both written-down guesses are wrong, then they both lose.

Cryptography in Wolfram

Okay that one seems kind of useless. But if someone wants to tell me otherwise I'm all ears! But this seems more like a stunt to introduce their new cloud service:

One of the main motivations for adding cryptographic functionality to the Wolfram Language was the arrival of the Wolfram Cloud.

Adios Hola!

If you haven't heard, some people from (or not) Lulzsec have found some serious vulns on the Hola! Plugin. And also they are not happy. Personally I find this Hola! really useful as a free solution to get a netflix US account when not in the US and being able to watch youtube (because everything is "blocked in your country" when you are not in the US). And the fact that you are basically a TOR node is also nice, it increases global anonymity! But that's just my opinion.

Elliptic Curve Playground

Play with elliptic curves!

MOAR?

You can find more on the links section. You can also suggest me links there =)

Hacking Week 2015 : Crypto 4 Write-Up posted June 2015

The Hacking Week ended 2 weeks ago and EISTI got the victory.

I'm the proud creator of the crypto challenge number 4, still available here, which was solved 12 times.

I also wrote a Proof of Solvableness, reading it should teach you about a simple and elegant crypto attack on RSA: the Same Modulus Attack.

(Note that I wrote that back in January)

Let's start

We are presentend with 4 files:

• alice.pub
• irc.log
• mykey.pem
• secret

the irc.log reads like this:

Session Start: Thu Feb 05 20:49:04 2015
Session Ident: #mastercsi
[20:49] * Now talking in #mastercsi
[20:49] * Topic is 'http://www.math.u-bordeaux1.fr/CSI/ |||| http://www.youtube.com/watch?v=zuDtACzKGRs   "das boot, ouh, ja" ||| http://www.koreus.com/video/chat-saut-balcon.html ||| http://blog.cryptographyengineering.com/ ||| http://www.youtube.com/watch?v=K1LZ60eMpiw ||| petit chat http://www.youtube.com/watch?v=eu2kVcWKvRo ||| sun : t'as le droit de boire quand même va'
[20:49] * Set by Jiss!~Jiss@2001:41d0:52:100::65d on Sat Nov 22 00:06:50
[20:49] <asdf> et donc j'ai chopé une vieille clé rsa qu'alice utilisait
[20:49] <qwer> alice la alice? tu te fous de moi ?
[20:49] <asdf> haha non
[20:49] <asdf> mais le truc est corrompu, ça a l'air de marcher pour chiffrer mais la moitié de la clé a disparu
[20:49] <qwer> attend j'ai sa clé publique qui traine quelque part, et même un fichier chiffré avec. me suis toujours demandé ce que c'était...
[20:50] <asdf> je t'ai envoyé le truc, mais ça m'étonnerait que ça soit la même clé non ?
[21:22] * Disconnected
Session Close: Thu Feb 05 21:22:11 2015

so alice.pub seems to be alice public rsa key. secret seems to be the file encrypted under this key and mykey.pem should be the partial key which was found.

Private-Key: (1024 bit)
modulus:
    00:c6:c8:35:29:a2:38:8f:14:63:65:c5:f5:fd:4b:
    0d:88:89:61:b9:5d:e1:0f:fa:88:53:a3:c2:cb:ed:
    75:0e:99:59:bd:0f:f8:72:c2:23:2f:6b:ad:32:62:
    4f:35:6a:82:d0:62:75:5e:1e:4f:ed:ae:54:e8:ca:
    24:71:fc:8d:13:ac:70:0e:e2:57:20:d4:d9:08:9f:
    d6:fb:d4:2f:12:e6:a4:1e:1c:1d:e8:1f:57:8c:32:
    13:2a:d0:85:94:e8:51:84:1d:02:39:cd:41:0d:ef:
    11:d1:c1:5e:e7:5b:92:f8:6a:04:f7:c6:c7:f3:6b:
    90:46:b8:fb:2f:e2:95:65:b1
publicExponent: 3 (0x3)
privateExponent:
    00:84:85:78:c6:6c:25:b4:b8:42:43:d9:4e:a8:dc:
    b3:b0:5b:96:7b:93:eb:5f:fc:5a:e2:6d:2c:87:f3:
    a3:5f:10:e6:7e:0a:a5:a1:d6:c2:1f:9d:1e:21:96:
    df:78:f1:ac:8a:ec:4e:3e:be:df:f3:c9:8d:f0:86:
    c2:f6:a8:5e:0b:ef:c0:ca:19:c5:e2:49:55:49:fe:
    e5:2e:51:3e:7b:e9:f2:22:07:d2:4b:84:7f:bb:0c:
    b5:ba:b7:95:c6:90:05:3e:65:2d:11:53:9a:2d:96:
    0f:ea:de:cb:9b:17:54:87:00:0f:78:12:ce:ac:f5:
    db:83:30:16:06:cc:35:7d:a3
prime1: 245 (0xf5)
prime2: 207 (0xcf)
exponent1: 163 (0xa3)
exponent2: 138 (0x8a)
coefficient: 189 (0xbd)

It looks like prime1, prime2 and some other stuff are pretty short. I guess this is what he meant by "half the key" is messed up.

By the way this is what a RSA PrivateKey should look like:

> RSAPrivateKey ::= SEQUENCE {
    version           Version,
    modulus           INTEGER,  -- n
    publicExponent    INTEGER,  -- e
    privateExponent   INTEGER,  -- d
    prime1            INTEGER,  -- p
    prime2            INTEGER,  -- q
    exponent1         INTEGER,  -- d mod (p-1)
    exponent2         INTEGER,  -- d mod (q-1)
    coefficient       INTEGER,  -- (inverse of q) mod p
    otherPrimeInfos   OtherPrimeInfos OPTIONAL
}

So this is what exponent1, exponent2 and coefficient are. Just additional information so that computations are faster thanks to CRT.

Let's ignore that for the moment.

$ openssl rsa -pubin -in alice.pub -modulus -noout
Modulus=C6C83529A2388F146365C5F5FD4B0D888961B95DE10FFA8853A3C2CBED750E9959BD0FF872C2232F6BAD32624F356A82D062755E1E4FEDAE54E8CA2471FC8D13AC700EE25720D4D9089FD6FBD42F12E6A41E1C1DE81F578C32132AD08594E851841D0239CD410DEF11D1C15EE75B92F86A04F7C6C7F36B9046B8FB2FE29565B1
$ openssl rsa -in mykey.pem -modulus -noout
Modulus=C6C83529A2388F146365C5F5FD4B0D888961B95DE10FFA8853A3C2CBED750E9959BD0FF872C2232F6BAD32624F356A82D062755E1E4FEDAE54E8CA2471FC8D13AC700EE25720D4D9089FD6FBD42F12E6A41E1C1DE81F578C32132AD08594E851841D0239CD410DEF11D1C15EE75B92F86A04F7C6C7F36B9046B8FB2FE29565B1

the partial key and alice public key seems to share the same modulus. this is vulnerable. If our public/private exponents are not messed up, this means we can factor the modulus and thus inverse Alice's public key.

Let's retrieve all the info we have and put them in a file:

openssl rsa -pubin -in alice.pub -modulus -noout | sed 's/Modulus=//' | xclip -selection c

Here's the modulus. We know that our public key is 3, let's get the private key in the clipboard as well

openssl asn1parse -in mykey.pem | grep 129 | tail -n1 | awk '{ print $7}' | sed 's/://' | xclip -selection c

here I parse mykey.pem with openssl. I select the lines I want with grep. It returns two results, the modulus and the private key. I select only the second line with tail. I select only the 7th column with awk. I remove the : with sed. And now I have a beautiful integer in my clipboard.

Okay so let's do a bit of Sage now:

# let's write the info we have
modulus = int(0xC6C83529A2388F146365C5F5FD4B0D888961B95DE10FFA8853A3C2CBED750E9959BD0FF872C2232F6BAD32624F356A82D062755E1E4FEDAE54E8CA2471FC8D13AC700EE25720D4D9089FD6FBD42F12E6A41E1C1DE81F578C32132AD08594E851841D0239CD410DEF11D1C15EE75B92F86A04F7C6C7F36B9046B8FB2FE29565B1)

public = 3
private = int(0x848578C66C25B4B84243D94EA8DCB3B05B967B93EB5FFC5AE26D2C87F3A35F10E67E0AA5A1D6C21F9D1E2196DF78F1AC8AEC4E3EBEDFF3C98DF086C2F6A85E0BEFC0CA19C5E2495549FEE52E513E7BE9F22207D24B847FBB0CB5BAB795C690053E652D11539A2D960FEADECB9B175487000F7812CEACF5DB83301606CC357DA3)

# now let's factor the modulus
k = (private * public - 1)//2
carre = 1
g = 2
while carre == 1 or carre == modulus - 1:
    g += 1
    carre = power_mod(g, k, modulus)

p = gcd(carre - 1, modulus) 
print(p)

This does not work. This should work.

Let's re-do the maths:

We know that our private and public keys cancel out. This is RSA:

private * public = 1 mod phi(N)

so we have private * public - 1 = 0 mod phi(N)

So for any g in our ring, we should have g^(private * public - 1) = 1 mod N

This is how RSA works.

Let's write it like that: private * public - 1 = k with k a multiple of phi(n). And we know that phi(n) = (p-1)(q-1) is even. So it could be written like this: k = 2^t * r with r an odd number.

Now if we take a random g mod N and we do g^(k/2) it should be the square root of a 1.

The Chinese Remainder Theorem tells us that there are 4 square roots mod N:

• 1 mod p
• -1 mod p
• 1 mod q
• -1 mod q

and two of them should be 1 mod N and -1 mod N. The 2 others should be different from 1 and -1 mod N. That's what I was trying to find in my code.

Once we have found this x mod N which is a square root of 1 mod N, we know that it is either x = 1 mod p or x = -1 mod p. If we are in the first case, we shoudl have x - 1 = 0 mod p which translates into x - 1 is a multiple of p. Doing gcd(x - 1, N) should give us p the first prime. If you don't understand it maybe check Dan Boneh's explanation (proof end of page 3) which should be clearer than mine.

With p it's easy to get q the other prime.

But it doesn't work...

Ah! I forgot that g^(k/2) could equal 1 all the time if k/2 were to be a multiple of phi(n). So let's code a loop that divides k by 2 and tries any g^k until it is giving us something else than 1. Then we know how many times we have to divide k by 2 so it's not a multiple of phi(n) anymore.

It turns out we just have to do it 3 times. And then it magically works. A bit more of Sage gives us the primes:

# p and q our primes
p = gcd(carre - 1, modulus) 
q = modulus // p

# now that we have factored N let's find alice decryption key
public = 65537
phi = (p - 1) * (q - 1)
private = inverse_mod(public, phi)

Now that we have Alice's private key there are two ways to decrypt our secret:

• recreate a valid rsa key with those values and use openssl rsautl
• figure out how openssl rsautl works to do it ourselves

Let's do the first one. We'll modify our mykey.pem for this:

openssl rsa -in  mykey.pem -outform DER -out newkey.bin
xxd -p newkey.bin > newkey.hex

we get this:

3082012202010002818100c6c83529a2388f146365c5f5fd4b0d888961b9
5de10ffa8853a3c2cbed750e9959bd0ff872c2232f6bad32624f356a82d0
62755e1e4fedae54e8ca2471fc8d13ac700ee25720d4d9089fd6fbd42f12
e6a41e1c1de81f578c32132ad08594e851841d0239cd410def11d1c15ee7
5b92f86a04f7c6c7f36b9046b8fb2fe29565b102010302818100848578c6
6c25b4b84243d94ea8dcb3b05b967b93eb5ffc5ae26d2c87f3a35f10e67e
0aa5a1d6c21f9d1e2196df78f1ac8aec4e3ebedff3c98df086c2f6a85e0b
efc0ca19c5e2495549fee52e513e7be9f22207d24b847fbb0cb5bab795c6
90053e652d11539a2d960feadecb9b175487000f7812ceacf5db83301606
cc357da3020200f5020200cf020200a30202008a020200bd

This is a DER encoding. One particular encoding from the ASN.1 family. It is a TLV kind of encoding (Type Lenght Value).

For example in:

02 8181 00c6c83529a2388f146365c5f5fd4b0d888961b95de10ffa8853
a3c2cbed750e9959bd0ff872c2232f6bad32624f356a82d062755e1e4fed
ae54e8ca2471fc8d13ac700ee25720d4d9089fd6fbd42f12e6a41e1c1de8
1f578c32132ad08594e851841d0239cd410def11d1c15ee75b92f86a04f7
c6c7f36b9046b8fb2fe29565b1

first is coded the type 02 (integer), then the length (81 repeated twice because the value block is bigger than 127bits, so we set the first byte to 81 (10000001, the first bit means it is a long way of defining the length, the 7 following bits are the number of byte it will take to define the length, in our case only one and it will be the next one) and the second byte to the actual size), then there is our modulo in hexadecimal. Note that the most significant bit of our value has to be zero if it is a positive integer, that's why we use 41 instead of 40 and lead the payload with 00.

So let's take the time and break this apart:

3082 // some header
0122 // the length of everything that follows (in byte)
0201 // integer of size 1
00 
028181 // integer of size 0x81 (our modulus)
00c6c83529a2388f146365c5f5fd4b0d888961b95de10ffa8853a3c2cbed750e9959bd0ff872c2232f6bad32624f356a82d062755e1e4fedae54e8ca2471fc8d13ac700ee25720d4d9089fd6fbd42f12e6a41e1c1de81f578c32132ad08594e851841d0239cd410def11d1c15ee75b92f86a04f7c6c7f36b9046b8fb2fe29565b1
0201 // integer of size 1 (our public key)
03
028181 // integer of size 0x81 (our private key)
00848578c66c25b4b84243d94ea8dcb3b05b967b93eb5ffc5ae26d2c87f3a35f10e67e
0aa5a1d6c21f9d1e2196df78f1ac8aec4e3ebedff3c98df086c2f6a85e0b
efc0ca19c5e2495549fee52e513e7be9f22207d24b847fbb0cb5bab795c6
90053e652d11539a2d960feadecb9b175487000f7812ceacf5db83301606
cc357da3
0202 // integer of size 2 (prime 1)
00f5
0202 // integer of size 2 (prime 2)
00cf
0202 // integer of size 2 (exponent 1)
00a3
0202 // integer of size 2 (exponent 2)
008a
0202 // integer of size 2 (coefficient)
00bd

Now let's remove everything which is after the modulus and let's refill the file with our own values. Let's go back in Sage to calculate them:

public = 65537
phi = (p - 1) * (q - 1)
private = inverse_mod(public, phi)
exponent1 = inverse_mod(private, p - 1)
exponent2 = inverse_mod(private, q - 1)
coefficient = inverse_mod(q, p)

After filling and modifying the header's length accordingly, we obtain a nice hexadecimal file that we can transform back to binary:

xxd -r -p new_key.hex | openssl asn1parse -inform DER

It works! So now let's decrypt with is shall we?

xxd -r -p new_key.hex | openssl rsa -inform DER -outform PEM -out newkey.pem
openssl rsautl -decrypt -in secret -inkey newkey.pem

We have our secret :)!

The Logjam Attack posted May 2015

Since it is now common custom to market a new vulnerability, here is the page: weakdh.org you will notice their lazyness in the non-use of a vulnerability logo.

The paper containing most information is here:

Imperfect Forward Secrecy: How Diffie-Hellman Fails in Practice, from a impressive amounts of experts (David Adrian, Karthikeyan Bhargavan, Zakir Durumeric, Pierrick Gaudry, Matthew Green, J. Alex Halderman, Nadia Heninger, Drew Springall, Emmanuel Thomé, Luke Valenta, Benjamin VanderSloot, Eric Wustrow, Santiago Zanella-Béguelin, Paul Zimmermann)

Not an implementation bug, flaw lives in the TLS protocol

This is not an implementation bug. This is a direct flaw of the TLS protocol.

This is also a Man in The Middle attack. By being in the middle, the attacker can modify the ClientHello packet to force the server to use an Export Ciphersuite, i.e. Export Ephemeral Diffie-Hellman, that uses weak parameters. I already explained what is an "Export" ciphersuite when the FREAK attack happened.

The server then generates weak parameters for a public key and sends 4 messages:

• ServerHello that specifies the Ciphersuite chosen from the list the Client gave him (if the attacker did things correctly, the server must have chosen an Export ciphersuite)
• Certificate which is the server's certificate
• ServerKeyExchange which contains the weak parameters and his public key.
• ServerHelloDone which signals the end of his transmission.

The ServerKeyExchange message is here because an "ephemeral" ciphersuite is used. So the Server and the Client need extra messages to compute an "ephemeral" key together. Using an Export DHE (Ephemeral Diffie-Hellman) or a normal DHE do not change the structure of the ServerKeyExchange message. And that's one of the problem since the server only signs this part with his long term public key.

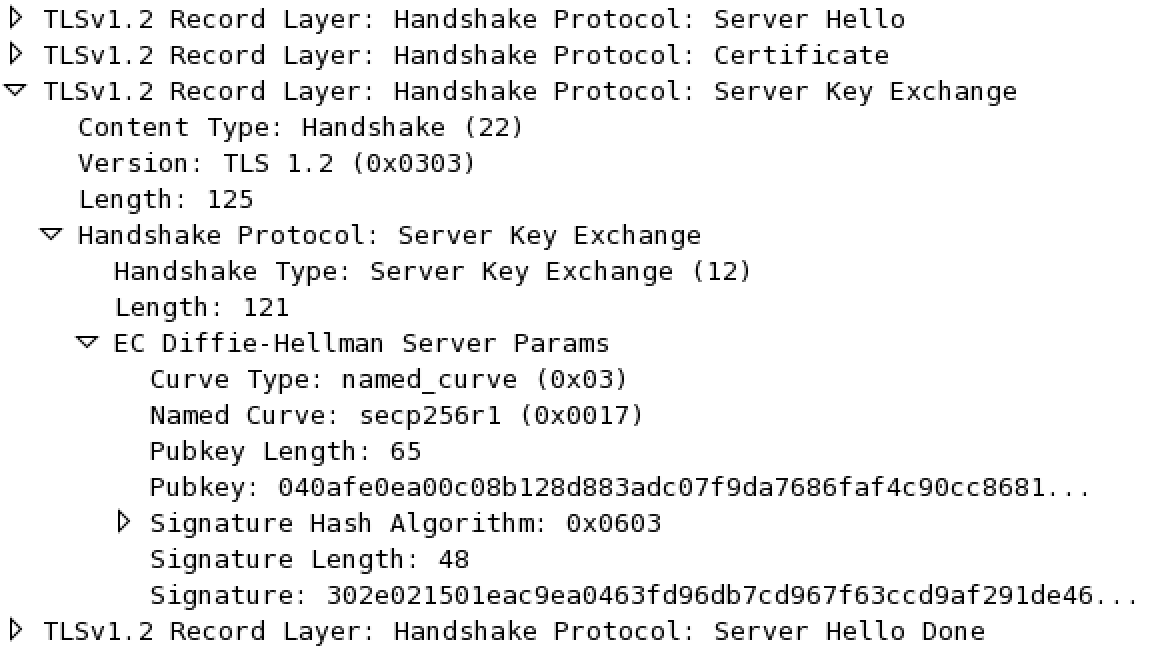
Here you can see the four messages in Wireshark, the signature is computed on the Client.Random, the Server.Random and the ECDH parameters contained in the ServerKeyExchange.

Thus, the attacker only has to modify the unsigned part of the ServerHello message to tell the Client his normal ciphersuite has been chosen (and not an Export ciphersuite).

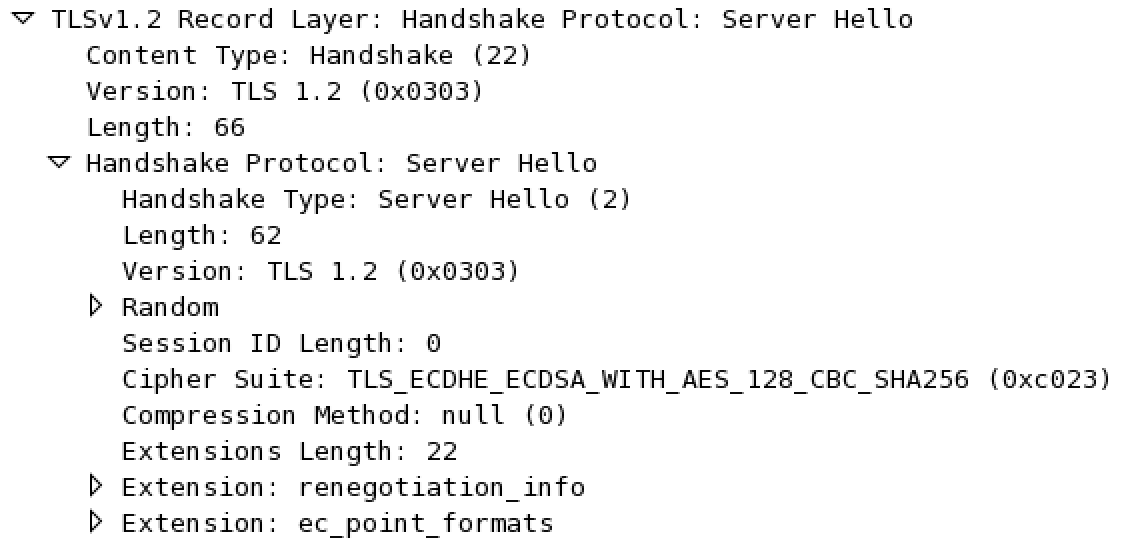
Now all the attacker has to do is to crack the private key of either the Client or the Server. Which is easy nowadays because of the low 512bits security of the Export DHE ciphersuite.

It can then pass as the server and read any messages the client wants to send to the server

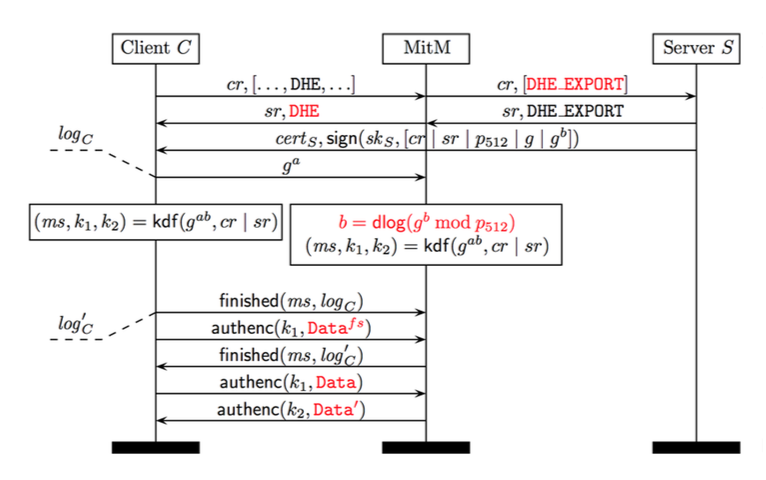
(taken from the paper)

Not an implementation bug, but implementations do help

the use of common DHE parameters is making things easier for attackers since they can do a pre-computation phase and use it to quickly crack a private key of a weak DHE parameters during the handshake.

This happens, for example when Apache hardcoded a prime for its Export DHE Ciphersuite that is now used in a bunch of servers

(taken from the paper)

Defense from the Server

Don't use common DH or DHE parameters! Generate your owns. But even more important, remove the Export Ciphersuites as soon as possible.

Defense from the Client

From a client perspective, the only defense is to reject small primes in DHE handshakes.

This is the only way of detecting this Man in The Middle attack.

You could also remove DHE in your ciphersuite list and try to use the elliptic curve equivalent ECDHE (Elliptic Curve Diffie-Hellman Ephemeral)

Another way: if you control both the server and the client, you could modify both ends so that the server signs the ciphersuite he chose, and the client verifies that as well.

1024 bits primes?

In the 1024-bit case, we estimate that such computations are plausible given nation-state resources, and a close reading of published NSA leaks shows that the agency’s attacks on VPNs are consistent with having achieved such a break. We conclude that moving to stronger key exchange methods should be a priority for the Internet community.

Seems like the NSA doesn't even need to downgrade you. So as a server, or as a client, you should refuse primes <= 1024bits

Where is TLS used?

TLS is not only used in https!

For example, what about EAP, i.e. wifi authentication? From a quick glance it looks like there are no export ciphersuite.

But weak DH and DHE parameters should be checked as well everywhere you make use of Discrete Logarithm crypto

Hacking Week 2015 posted May 2015

The Hacking week just started, it's a CTF that happens over a week.

You'll find challenges about crypto, network, forensic, reverse and exploit.

And also, I have a challenge up there in the crypto challenge ^^

It's in french here: http://hackingweek.fr/challenges/ (click on "voir" next to crypto 4)

basically Alice encrypted the secret, you have to find what the secret is. What you have is a key that shares the same modulus as Alice.

How to compare password hashes in PHP? posted May 2015

The wierdness of ==

Do you know what happens when you run this code in PHP?

<?php
var_dump(md5('240610708') == md5('QNKCDZO'));
var_dump(md5('aabg7XSs') == md5('aabC9RqS'));
var_dump(sha1('aaroZmOk') == sha1('aaK1STfY'));
var_dump(sha1('aaO8zKZF') == sha1('aa3OFF9m'));
var_dump('0010e2' == '1e3');
var_dump('0x1234Ab' == '1193131');
var_dump('0xABCdef' == '     0xABCdef');
?>

Check the answer here. That's right, everything is True.

This is because == doesn't check for type, if a string looks like an integer it will first try to convert it to an integer first and then compare it.

More about PHP == operator here

This is weird and you should use === instead.

Even better, you can use hash_equals (coupled with crypt)

Compares two strings using the same time whether they're equal or not.
This function should be used to mitigate timing attacks; for instance, when testing crypt() password hashes.

Here's the example from php.net:

<?php
$expected  = crypt('12345', '$2a$07$usesomesillystringforsalt$');
$correct   = crypt('12345', '$2a$07$usesomesillystringforsalt$');
$incorrect = crypt('apple',  '$2a$07$usesomesillystringforsalt$');

hash_equals($expected, $correct);
?>

Which will return True.

But why?

the hashed strings start with 0e, for example both strings are equals in php:

md5('240610708') = 0e462097431906509019562988736854
md5('QNKCDZO')   = 0e830400451993494058024219903391

because php understands them as both being zero to the power something big. So zero.

Security

Now, if you're comparing unencrypted or unhashed strings and one of them is supposed to be secret, you might have potentialy created the setup for a timing-attack.

Always try to compare hashes instead of the plaintext!

Previous Links posted April 2015

There is a Link section here that is not very visible, I don't really know how I could show its content on the frontpage here. But here's one way:

May 21th

• Its HUGE - RSA 2015

• Montgomery modular multiplication

• Residue number system

• Improving the security of our users on Wikimedia sites

May 22th

• RSA Key Extraction via Low-Bandwidth Acoustic Cryptanalysis

May 23th

• ransomware decryptor

• Security strength of RSA in relation with the modulus size

• Measuring SSL Performance: RSA keys

• * [tor-talk] SIGAINT email service targeted by 70 bad exit nodes

May 24th

• SSL Labs RC4 Deprecation Plan

• 11.3 Why doesn’t GnuPG default to using RSA-4096?

May 25th

• Multi-million EU project to protect data against quantum computers

May 27th

• Practical Race Condition Vulnerabilities in Web Applications

• Why You Should Add Joern to Your Source Code Audit Toolkit

• A gentle introduction to elliptic-curve cryptography

• Eurocrypt 2015: Universal Signature Aggregators

• A Lesson In Timing Attacks (or, Don’t use MessageDigest.isEquals)

May 28th

• Advanced cryptographic ratcheting

• Vault - a tool for managing secrets

• What happens when you hit Ctrl-C?

• What are the advantages of elliptic curve cryptography using binary fields over prime fields and vice versa?

More

And you can find more on the Links section of this blog