Quick access to articles on this page:
more on the next page...
I've polished the design of this blog a bit (with flexbox and css-grid!) and it should look a bit cleaner :)
I've also created a page for graphics. I only have 3 at the moment, but I know that PHD students often present posters like these at conferences so if you know any (or if you have one yourself) and you want me to showcase it there send me a message!

I'm giving a talk at Black Hat Europe in a few months, and thus I was given two tickets for students to come attend the conference for free.
Anyone interested?
EDIT: no more tickets! If you really want to go to Black Hat, I'd advise you to contact directly other speakers as every BH speaker is given 2 free pass for students.
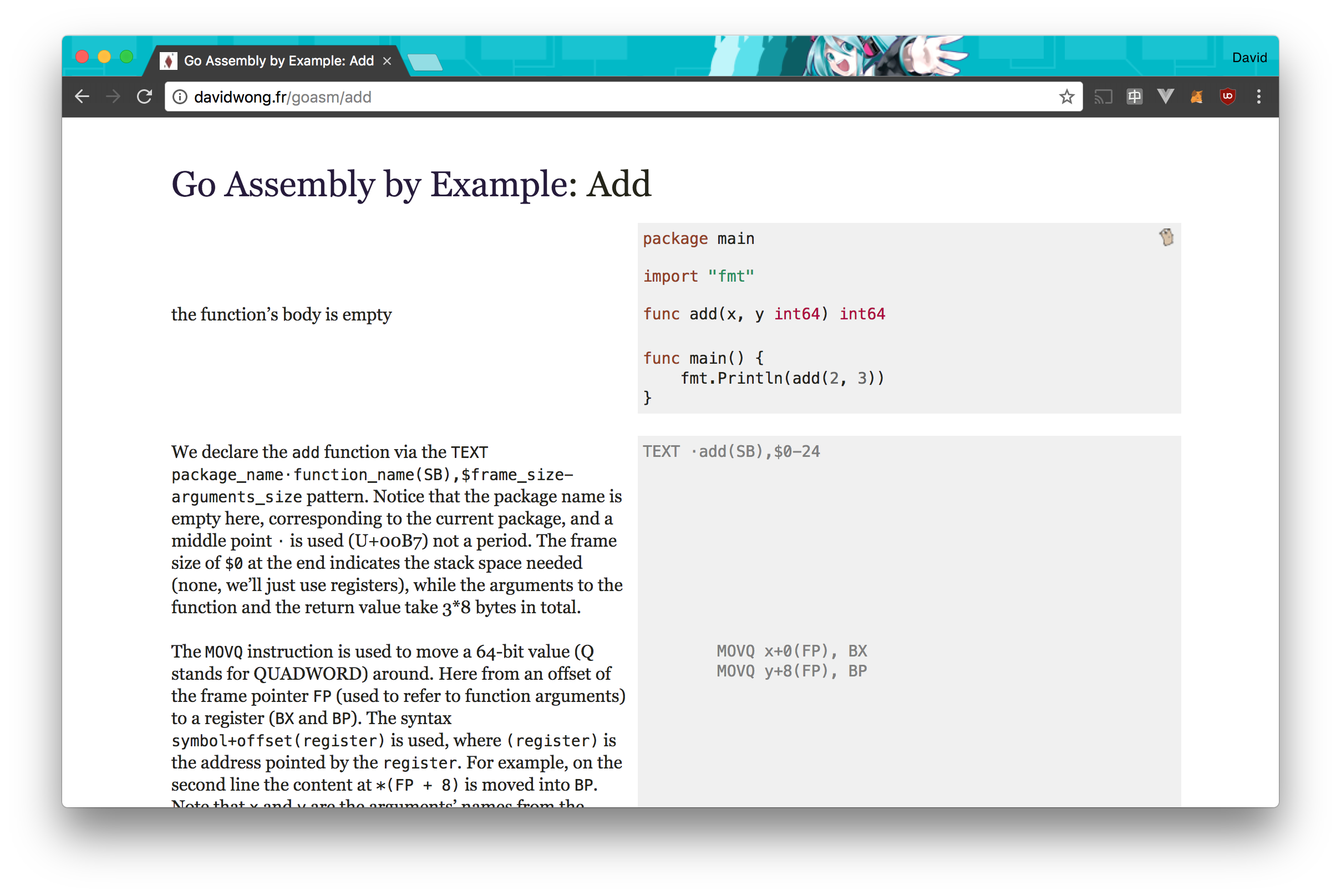
In my quest to understand Go Assembly better, I forked Go by Example and created my own version for Go Assembly.
You can check it out here, and someone already translated it in Chinese here.
tl;dr: use this code
When a program uses a secret key for some cryptographic operation, it will store it somewhere in memory. This is a problem because it is trivial to read what has been previously stored in memory from a different program, just create something like this:
#include <stdio.h>
int main(){
unsigned char a[5000];
for(int i = 0; i < 10000; i++) {
printf("x", a[i]);
}
printf("\n");
}
This will print out whatever was previously there in memory, because the buffer a is not initialized to zeros. Actually, C seldom initializes things to zeros, it can if you specifically use something like calloc instead of malloc or static in front of a global variable/struct/...
EDIT: as Fred Akalin pointed to me, it looks like this is fixed in most modern OS. Colin Perceval notes that there are other issues with not zero'ing memory:
if someone is able to exploit an unrelated problem — a vulnerability which yields remote code execution, or a feature which allows uninitialized memory to be read remotely, for example — then ensuring that sensitive data (e.g., cryptographic keys) is no longer accessible will reduce the impact of the attack. In short, zeroing buffers which contained sensitive information is an exploit mitigation technique.
This is a problem.
To remove a key from memory, developers tend to write something like this:
memset(private_key, 0, sizeof(*private_key));
Unfortunately, when the compiler sees something like this, it will remove it. Indeed, this code is useless since the variable is not used anymore after, and the compiler will optimize it out.
How to fix this issue?
A memset_s function was proposed and introduced in C11. It is basically a safe memset (you need to pass in the size of the pointer you're zero'ing as argument) that will not get optimized out. Unfortunately as Martin Sebor notes:
memset_s is an optional feature of the C11 standard and as such isn't really portable. (AFAIK, there also are no conforming C11 implementations that provide the optional Annex K in which the function is defined.)
To use it, a #define at the right place can be used, and another #define is used as a notice that you can now use the memset_s function.
#define __STDC_WANT_LIB_EXT1__ 1
#include <string.h>
#include <stdlib.h>
// ...
#ifdef __STDC_LIB_EXT1__
memset_s(pointer, size_data, 0, size_to_remove);
Unfortunately you cannot rely on this for portability. For example on macOS the two #define are not used and you need to use memset_s directly.
Martin Sebor adds in the same comment:
The GCC -fno-builtin-memset option can be used to prevent compatible compilers from optimizing away calls to memset that aren't strictly speaking necessary.
Unfortunately, it seems like macOS' gcc (which is really clang) ignores this argument.
What else can we do?
I asked Robert Seacord who always have all the answers, here's what he gave me in return:
void *erase_from_memory(void *pointer, size_t size_data, size_t size_to_remove) {
if(size_to_remove > size_data) size_to_remove = size_data;
volatile unsigned char *p = pointer;
while (size_to_remove--){
*p++ = 0;
}
return pointer;
}
Does this volatile keyword works?
Time to open gdb (or lldb) to verify what the compiler has done. (This can be done after compiling with or without -O1, -O2, -O3 (different levels of optimization).)
Let's write a small program that uses this code and debug it:
int main(){
char a[6] = "hello";
printf("%s\n", a);
erase_from_memory(a, 6, 6);
}
- we open gdb with the program we just compiled
- we set a break point on
main
- we run the program which will stop in
main
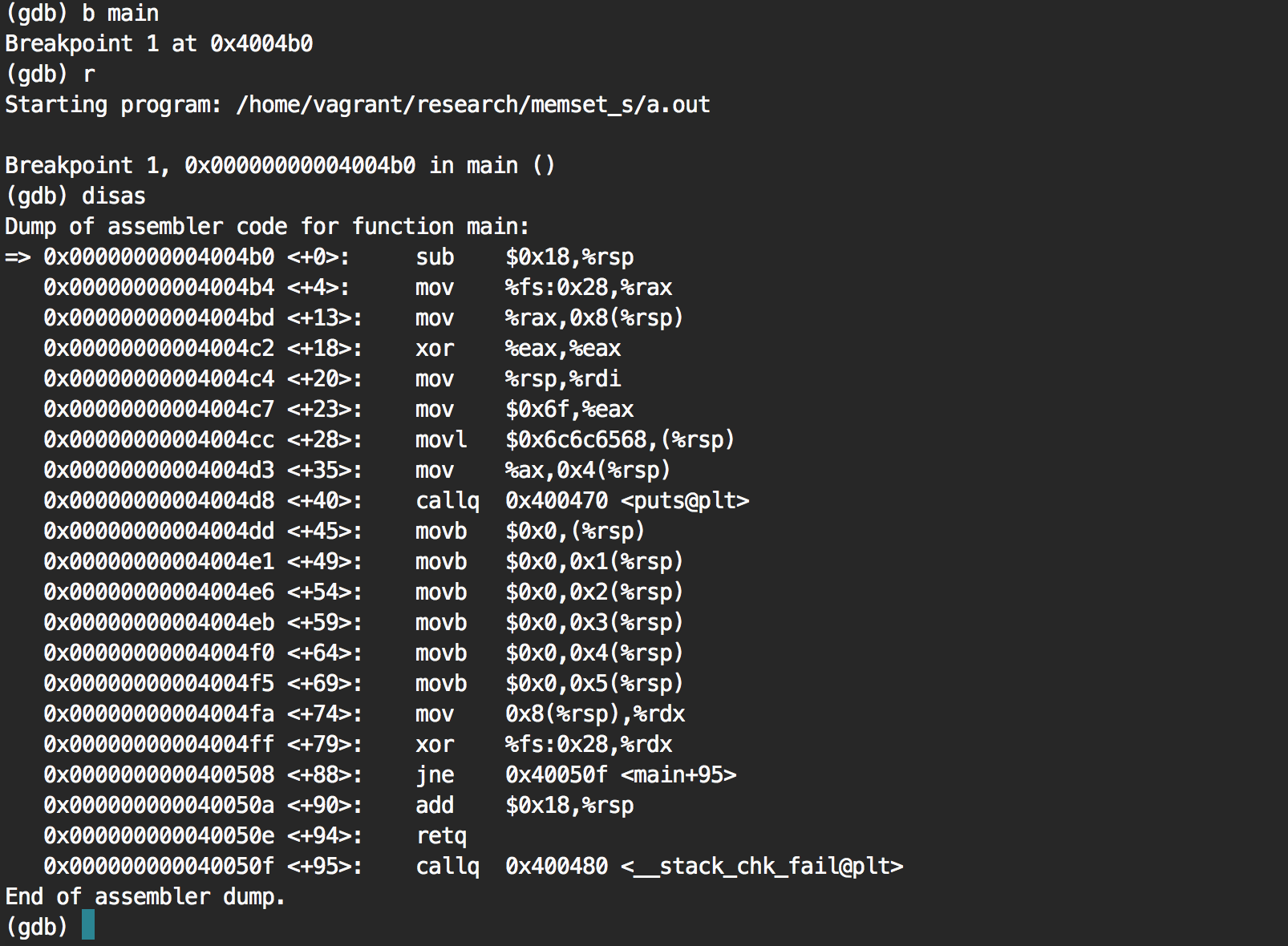
We notice a bunch of movb $0x0 ...
Is this it? Let's put a breakpoint on the first one and see what the stack pointer (rsp) is pointing to.
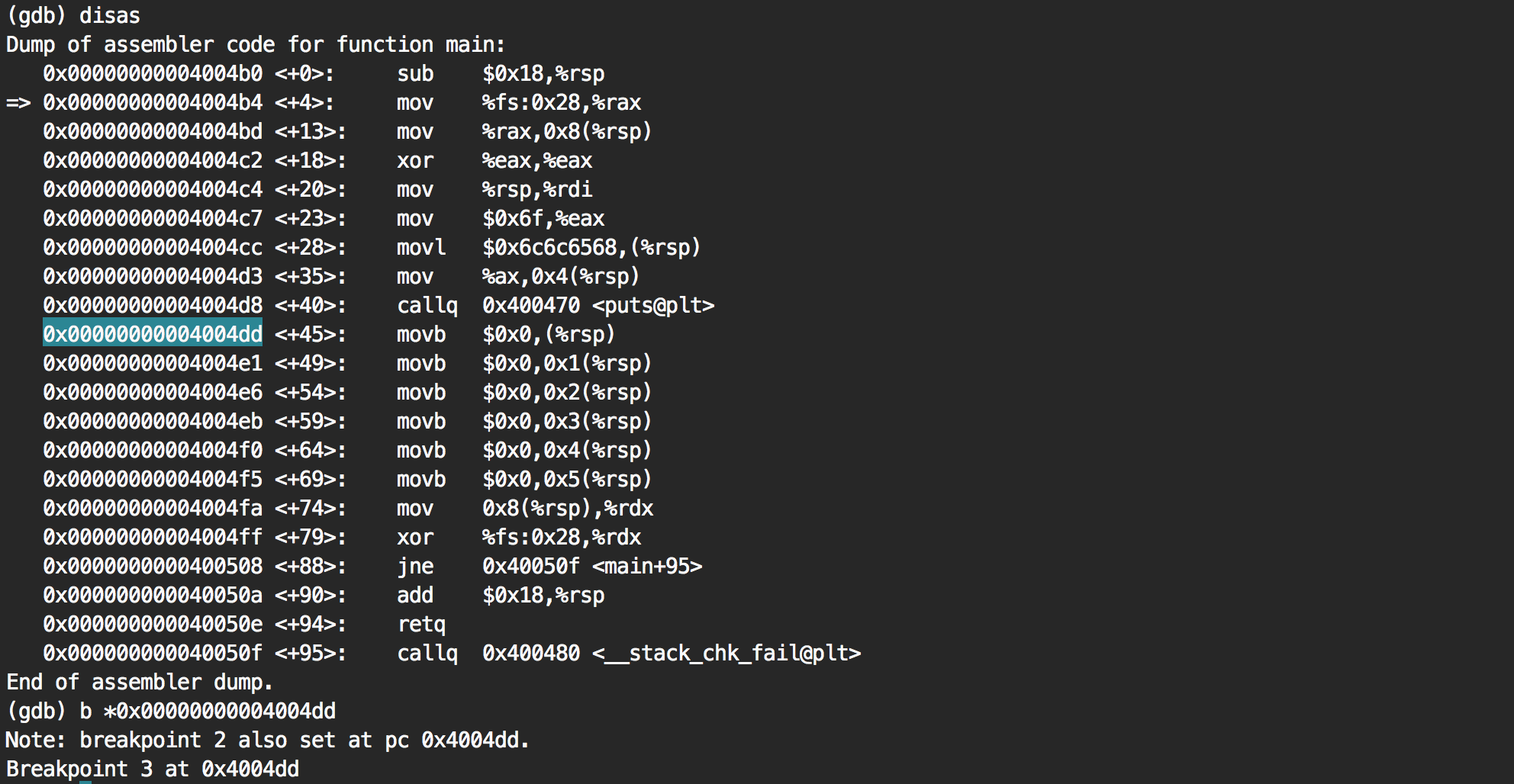
It's pointing to the string "hello" as we guessed.
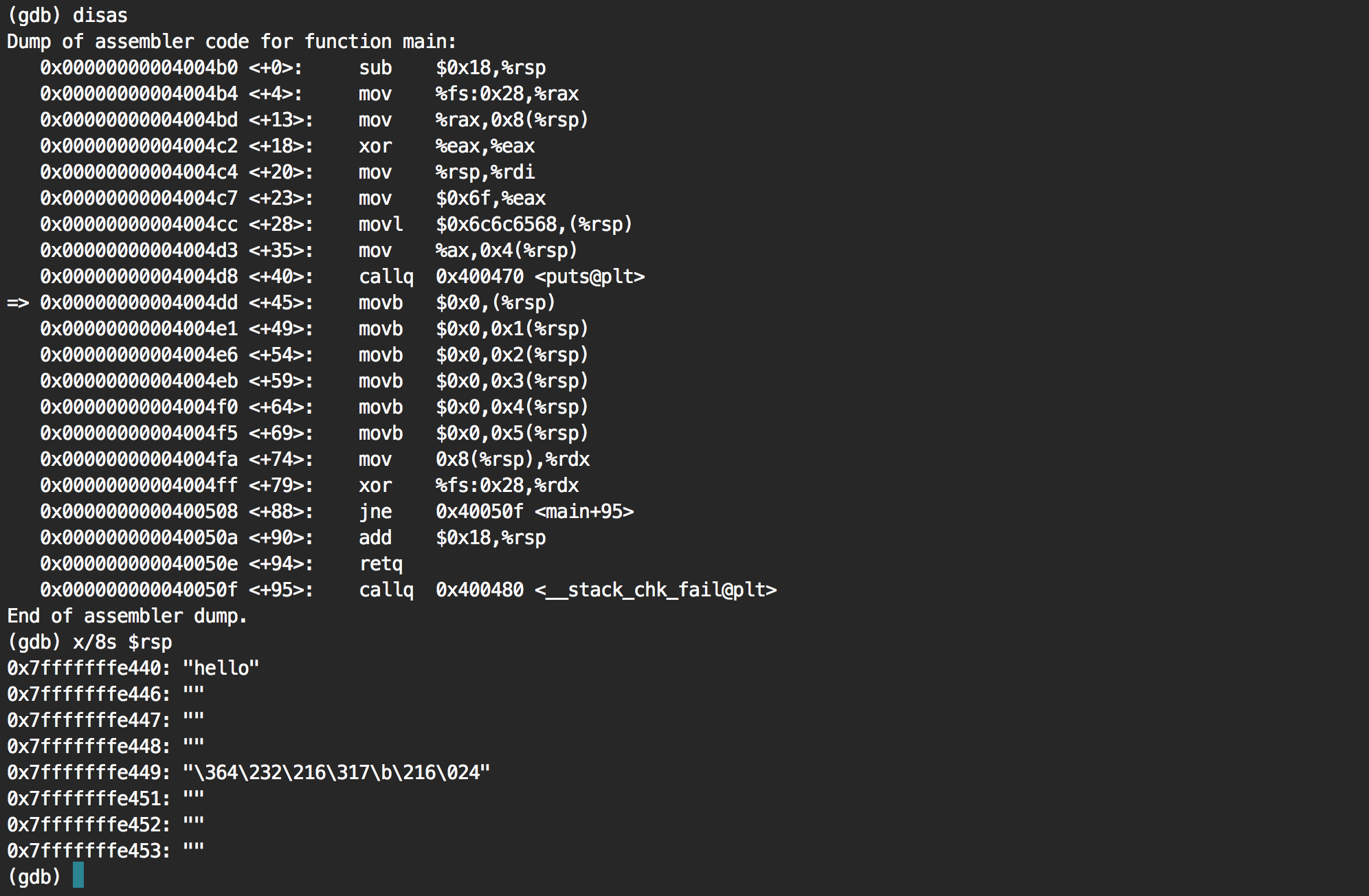
Going to the next instruction via ni, we can then see that the first letter h has been removed. Going over the next instructions, we see that the full string end up being zero'ed.
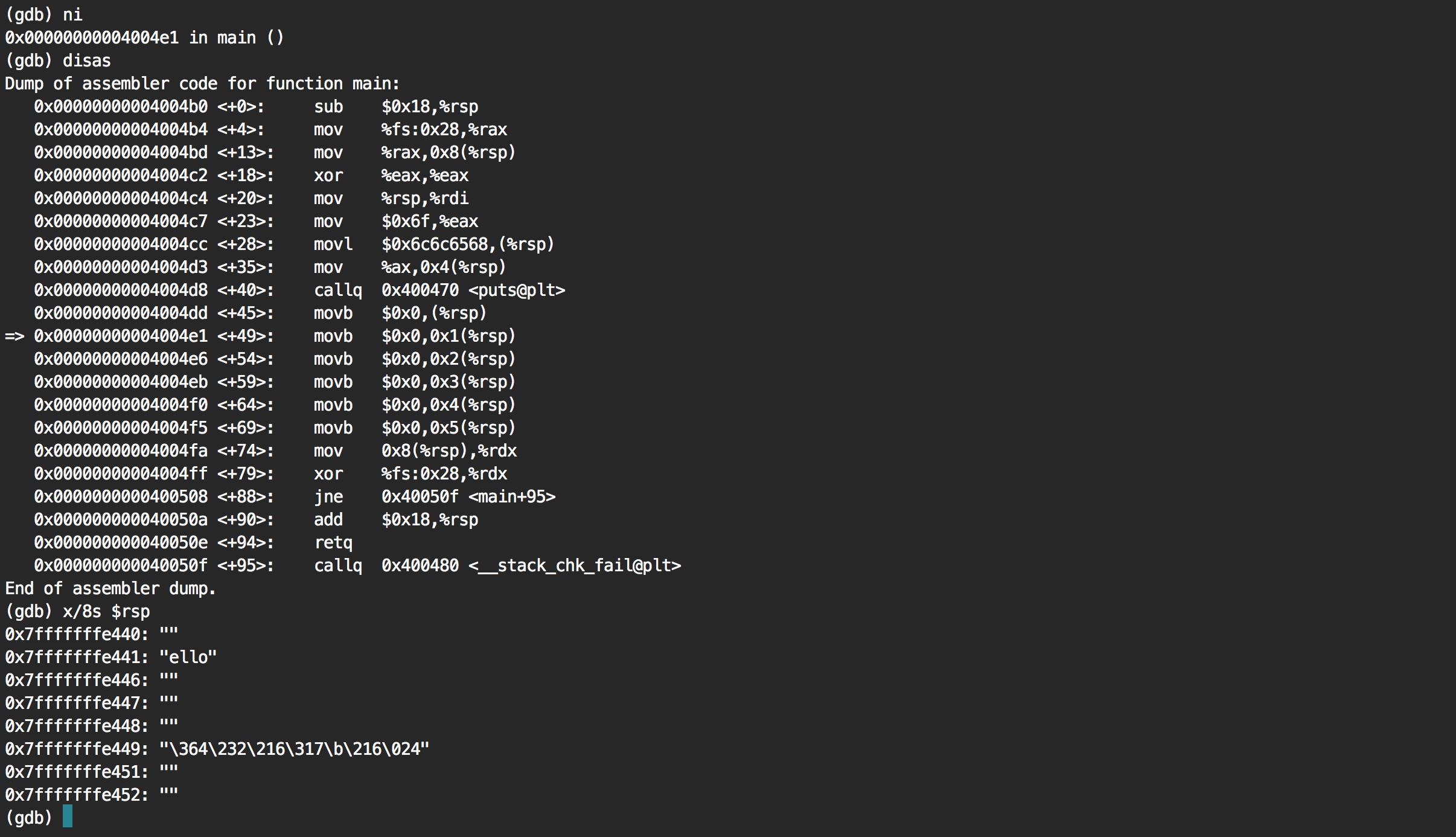
It's a success!
The full code can be seen here as an erase_from_memory.h header file that you can just include in your codebase:
#ifndef __ERASE_FROM_MEMORY_H__
#define __ERASE_FROM_MEMORY_H__ 1
#define __STDC_WANT_LIB_EXT1__ 1
#include <stdlib.h>
#include <string.h>
void *erase_from_memory(void *pointer, size_t size_data, size_t size_to_remove) {
#ifdef __STDC_LIB_EXT1__
memset_s(pointer, size_data, 0, size_to_remove);
#else
if(size_to_remove > size_data) size_to_remove = size_data;
volatile unsigned char *p = pointer;
while (size_to_remove--){
*p++ = 0;
}
#endif
return pointer;
}
#endif // __ERASE_FROM_MEMORY_H__
Many thanks to Robert Seacord!
PS: here is how libsodium does it
EDIT: As Colin Percival wrote here, this problem is far from being solved. Secrets can get copied around in (special) registers which won't allow you to easily remove them.
Loup Vaillant wrote a good blog post about his new crypto library Monocypher.
In spite of the obvious controversy of launching a new crypto library, I really like it. Note that this is not me officially endorsing the library, I just think it's cool and I would only consider using it after it had matured a bit more.
The whole thing is one ~1500LOC file and is pretty clear to read. It only implements a few crypto functions.
The blog post mentions a few bugs that were found in his library (and I appreciate how open he is about it). Here's an interesting one:
Bug 5: signed integer overflow
This one was sneaky. I wouldn't have caught it without UBSan.
I was shifting a uint8_t, 24 bits to the left. I failed to realise that integer promotion means this unsigned byte would be converted to a signed integer, and overflow if the byte exceeded 127. (Also, on crazy platforms where integers are smaller than 32 bits, this would never have worked.) An explicit conversion to uint32_t did the trick.
At this point, I was running the various sanitisers just to increase confidence. Since I used Valgrind already, I didn't expect to actually catch a bug. Good thing I did it anyway.
Lesson learned: Never try anything serious in C or C++ without sanitisers. They're not just for theatrics, they catch real bugs.
This is the problem patched.

Simplified, the bad code really looks like this:
uint32_t = uint8_t << 8 * i;
And all the theory behind the problem can be dismissed, if he had written his code with precautions. When I see something like this, the first thing I think about is that it should probably be written like this:
uint32_t = (uint32_t)uint8_t << 8 * i;
This would avoid any weird C problems as a casting (especially to a bigger type) usually goes fine.
OK but what was the problem with the above code?
Well, in C some operations will usually promote the type to something bigger. See the C standard:
shift-expression << additive-expression
The integer promotions are performed on each of the operands
What is an integer promotion? See the C standard:
If an int can represent all values of the original type, the value is converted to an int;
otherwise, it is converted to an unsigned int.
These are called the integer promotions
So looking back at our bad snippet:
uint32_t = uint8_t << 8 * i;
- the maximum value of
uint8_t is 255, which can largely be hold in a signed int of 16-bit or 32-bit (depends on the architecture). So 01 is promoted to 00 00 00 01 if a signed int is 32-bit (which it probably is). (In the case were we would have been dealing with a uint32-t, there would have been no problems as "big" values that cannot be represented in a signed int of 32-bit would have been promoted to a unsigned int instead of a signed int.)
- the bits are shifted on the left. For example of 8 places
00 00 01 00.
- the result gets casted to uint32_t. We still get
00 00 01 00.
This doesn't look like an issue, and it probably isn't most of the time. Now imagine if in 1. our value was 80 (which is 1000 0000 in bits).
Imagine now that in 2. we shift it of 24 bits on the left, that will give us 80 00 00 00 which is an all zero bitstring except for the most significant bit (MSB). In an int type the MSB is the signing bit. I believe at this point, the value will be automatically sign extended to the size of the register, so in your 64-bit machine it will be saved as ff ff ff ff 80 00 00 00.
Now in 3. The result now get casted to a uint32_t. Which doesn't do anything but change the value of the pointer. But we now have a wrong result! What we wanted here was 00 00 00 00 80 00 00 00. If you're not convinced, you can run the following script on your computer:
#include <stdio.h>
#include <stdint.h>
int main(){
uint8_t start = -1;
printf("%x\n", start); // prints 0xff
uint64_t result = start << 24;
printf("%llx\n", result); // should print 00000000ff000000, but will print ffffffffff000000
result = (uint64_t)start << 24;
printf("%llx\n", result); // prints 00000000ff000000
return 0;
}
Looking at the binary in Hopper we can see this:

And we notice the movsxd instruction which is "move doubleword to quadword with sign-extension".
It moves the result of the shift left (shl) into a register, making sure that its result is the same for an int64_t which is the maximum value your register can hold.
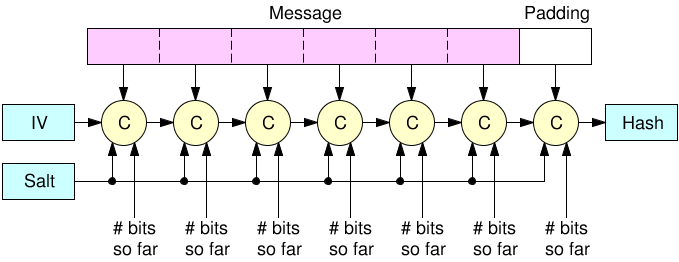
If you don't know about length extension attacks, it is a very simple and straight forward attack that let you forge a new hash by extending another one, letting you pretend that hashing had previously not been terminated.
The attack targets such hashes: SHA-256(key | message) where the key is secret and where | means concatenation.
This is because a SHA-2 hash (unless we're talking about the truncated versions) is literally a full copy of the state of the hash. It is not the state of hashing key and message, but rather key and message and some padding. Because like everything in the symmetric crypto world you need to pad to the block size. I believe this is 512 bits in the Secure Hash Algorithm 2.
The attack lets you take such a hash, and continue the hashing to obtain the hash of key | message | padding | more where more is whatever you want. And all of this without any knowledge of the secret key!
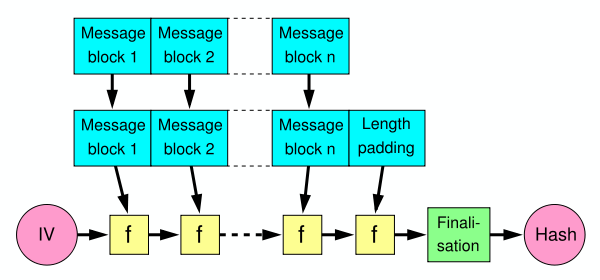
Interestingly, this comes from the way the Merkle-Damgard construction is applied (without a good finalization function). And because of this hash functions like MD4, MD5, SHA-1 and SHA-2 have all suffered from the same issues. You'd be glad to hear that this issue is fixed in any of the SHA-3 contestant (read: BLAKE2 and SHAKE and SHA-3 are fine). Keccak (SHA-3's winner) fixes it by using a Sponge construction, not letting you see a big part of the state (the capacity) while BLAKE2 fixes it by using the HAsh Iterative FrAmework (HAIFA), using a "number of bits hashed so far" (not including the padding) inside of the compression function.
While looking at the exact date length extension attacks were found (which I couldn't find), Samuel Neves came up with an interesting response.
It looks like the NIST was made aware, during the standardization process of SHA-2, that simple fixes would prevent length extension attacks.
This comment from John Kelsey (who later joined the NIST) is from 28 august 2001 (by the way it doesn't make sense to write dates as month/day/year. Nobody can understand it outside of the US. We have an ISO format that specifies a logical year-month-day). In it he talks about the attack, and proposes a simple fix:
Niels Ferguson suggested the following simple fix to me, some time ago: Choose some nonzero constant C0, of the same size as the hash function chaining variable. Hash messages normally, until we come to the last block in the padded message. XOR C0 into the chaining variable input into that last compression function computation. The resulting compression function output is used as the hash result. For concreteness, I propose C0 = 0xa5a5...a5, with the 0xa5 repeated until every byte is filled in. This should be interpreted in little-endian bit ordering.
Why did the NIST ignore this when it could have modified the draft before publication? I have no idea. Is this one more fuck up from their part?
Introduction
The Strobe Protocol Framework is a specification, available here, which you can use to implement a primitive called the Strobe Duplex Construction. The implemented Strobe object should respond to a dozen of calls that can be combined together to allow you to generate random numbers, derive keys, hash, encrypt, authenticate, and even build complex symmetric protocols.
The thing is sexy for several reasons:
- you only use a single primitive to do all of your symmetric crypto
- it makes the code size of your library extremely small, easy to fit in embedded devices and easy to audit
- on top of that it allows you to create TLS-like protocols
- every message/operation of your protocol depends on all the previous messages/operations
The last one might remind you of Noise which is a protocol framework as well that mostly focus on the asymmetric part (handshake). More on that later :)
Overview
From a high level point of view, here is a very simple example of using it to hash a string:
myHash = Strobe_init("hash")
myHash.AD("something to be hashed")
hash = myHash.PRF(outputLen=16)
You can see that you first instantiate a Strobe object with a custom name. I chose "hash" here but it could have been anything. The point is to personalize the result to your own protocol/system: initializing Strobe with a different name would give you a different hash function.
Here two functions are used: AD and PRF. The first one to insert the data you're about to hash, the second one to obtain a digest of 16 bytes. Easy right?
Another example to derive keys:
KDF = Strobe_init("deriving keys for something")
KDF.KEY(keyInput)
key1 = KDF.PRF(outputLen=16)
key2 = KDF.PRF(outputLen=16)
Here we use a new call KEY which is similar to AD but provides forward-secrecy as well. It is not needed here but it looks nicer and so I'll use it. We then split the output in two in order to form two new keys out of our first one.
Let me now give you a more complex example. So far we've only used Strobe to create primitives, what if I wanted to create a protocol? For example on the client side I could write:
myProtocol = Strobe_init("my protocol v1.0")
myProtocol.KEY(sharedSecret)
buffer += myProtocol.send_ENC("GET /")
buffer += myProtocol.send_MAC(len=16)
// send the buffer
// receive a ciphertext
message = myProtocol.recv_ENC(ciphertext[:-16])
ok = myProtocol.recv_MAC(ciphertext[-16:])
if !ok {
// reset the connection
}
Since this is a symmetric protocol, something similar should be done on the server side.
The code above initializes an instance of Strobe called "my protocol v1.0", and then keys it with a pre-shared secret or some key exchange output. Whatever you like to put in there. Then it encrypts the GET request and sends the ciphertext along with an authentication tag of 16 bytes (should be enough). The client then receives some reply and uses the inverse operations to decrypt and verify the integrity of the message. This is what the server must have done when it received the GET request as well. This is pretty simple right?
There's so much more Strobe can do, it is up to you to build your own protocol using the different calls Strobe provides. Here is the full list:
- AD: Absorbs data to authenticate.
- KEY: Absorbs a key.
- PRF: Generates a random output (forward secure).
- send_CLR: Sends non-encrypted data.
- recv_CLR: Receives non-encrypted data.
- send_ENC: Encrypts data.
- recv_ENC: Decrypts data.
- send_MAC: Produces an authentication tag.
- recv_MAC: Verifies an authentication tag.
- RATCHET: Introduce forward secrecy.
There are also meta variants of some of these operations which allow you to specify that what you're operating on is some frame data and not the real data itself. But this is just a detail.
How does it work?
Under its surface, Strobe is a duplex construction. Before I can explain that, let me first explain the sponge construction.
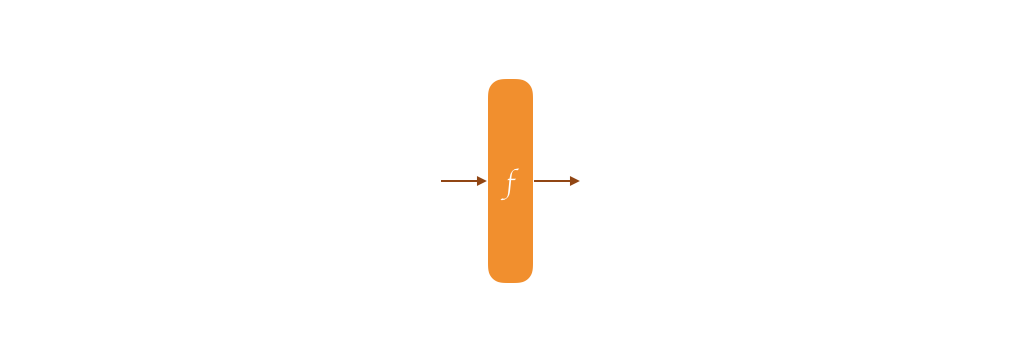
A sponge belongs to a field in cryptography called permutation-based cryptography. This is because at its core, it works on top of a permutation. The whole security of the thing is proven as long as your permutation is secure, meaning that it behaves like a random oracle. What's a permutation? Oh sorry, well, imagine the AES block cipher with a fixed key of 00000000000000000. It takes all the possible inputs of 128-bit, and it will give you all the possible outputs of 128-bit. It's a one-to-one mapping, for one plaintext there is always one ciphertext. That's a permutation.
SHA-3 is based on the sponge construction by the way, and it uses the keccak-f[1600] permutation at its core. Its security was assessed by long years of cryptanalysis (read: people trying to break it) and it works very similarly as AES: it has a series of steps that modify an input, and these steps are repeated many many times in what we call rounds. AES-128 has 10 rounds, Keccak-f[1600] has 24 rounds. The 1600 part of the name means that it has an input/ouput size of 1600 bits.

So here our permutation is Keccak-f[1600], and we imagine that our input/output is divided into two parts: the public part (rate) and the secret part (capacity). Intuitively we'll say that the bigger the secret part is, the more secure the construction is. And indeed, SHA-3 has several flavors that will use different sizes according to the security advertised.
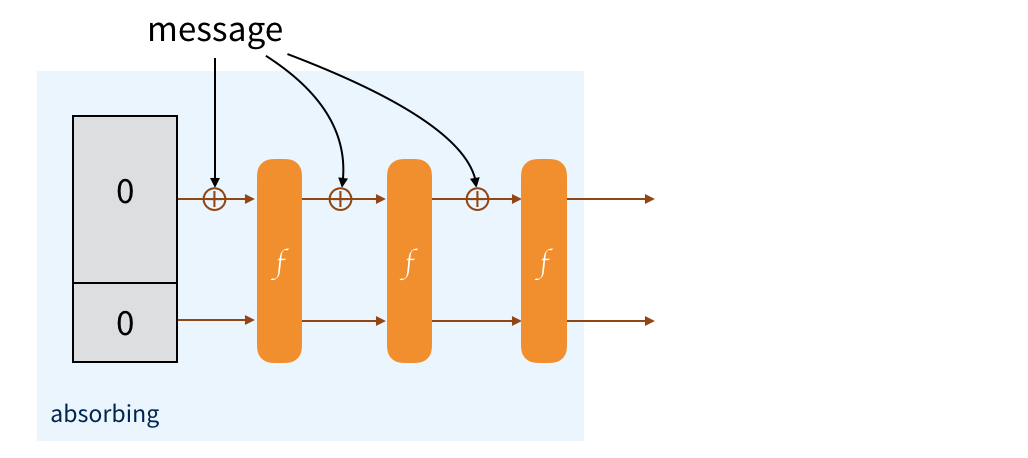
The message is padded and split into multiple blocks of the same size as the public part. To absorb them into our sponge, we just XOR each blocks with the public part of the state, then we permute the state.
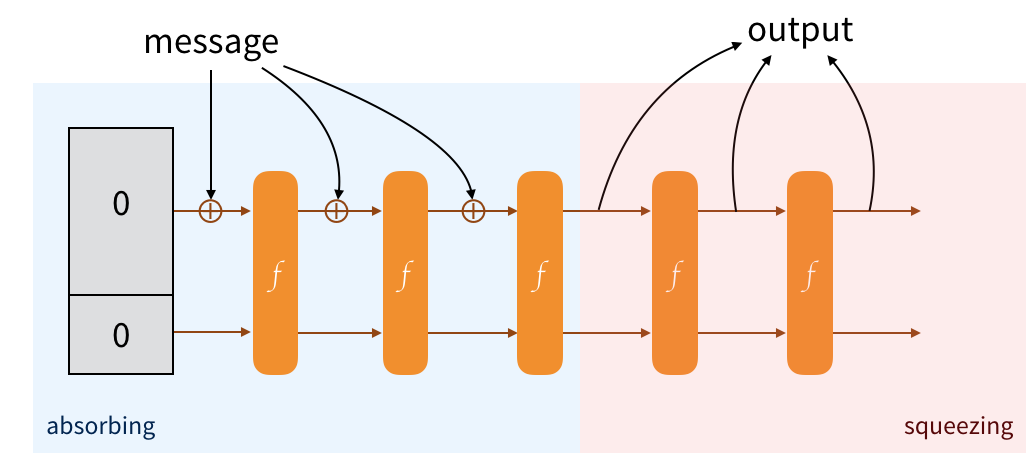
To obtain an output from this construction, we just retrieve the public part of our state. If it's not enough, we permute to modify the state of the sponge, then we collect the new public part so that it can be appended to the previous one. And we continue to do that until we have enough. If it's too much we truncate :)
And that's it! It's a sponge, we absorb and we squeeze. Makes sense right?
This is exactly how SHA-3 works, and the output is your hash.
What if we're not done though? What if we want to continue absorbing, then squeeze again, then absorb again, etc... This would give us a nice property: everything that we squeeze will depend on everything that has been absorbed and squeezed so far. This provides us transcript consistency.
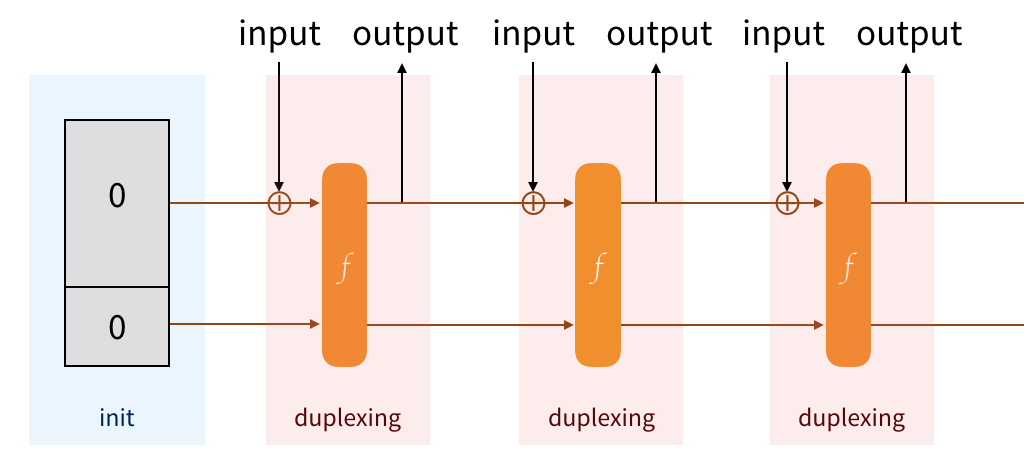
The Keccak team said we can, and they created the Duplex construction. It's just something that allows us to absorb, to squeeze, to absorb, to squeeze, and on and on...
Building Strobe
"How is Strobe constructed on top of the Duplex construction?" you may ask. And I will give you an intuition of an answer.
Strobe has fundamentally 3 types of internal operations, that are used to build the operations we've previously saw (KEY, AD, Send_ENC, ...). They are the following:
- default:
state = input ⊕ state
- cbefore:
state = input
- cafter:
output, state = input ⊕ state
The default one simply absorbs the input with the state. This is useful for any kind of operation since we want them to affect the outcome of the next ones.
The cbefore internal operation allows you to replace the bits of the state with your input. This is useful when we want to provide forward-secrecy: if the state is later leaked, the attacker will not be able to recover a previous state since bits of the rate have been erased. This is used to construct the KEY, RATCHET and PRF operations. While KEY replaces the state with bits from a key, RATCHET and PRF replaces the state with zeros.
cafter is pretty much the same as the default operation, except that it also retrieves the output of the XOR. If you've seen how stream ciphers or one-time pads work, you might have recognized that this is how we can encrypt our plaintext. And if it wasn't more obvious to you, this is what will be used to construct the Send_ENC operations.
There is also one last thing: an internal flag called forceF that allows you to run the permutation before using any one of these internal operations. This is useful when you need to produce something from the Duplex construction: a ciphertext, a random number, a key, etc... Why? Because we want the result to depend on what happened previously, and since we can have many operations per block size we need to do this. You can imagine problems if we were not to do that: an encryption operation that would not depend on the previously inserted key for example.
Let's see some examples!
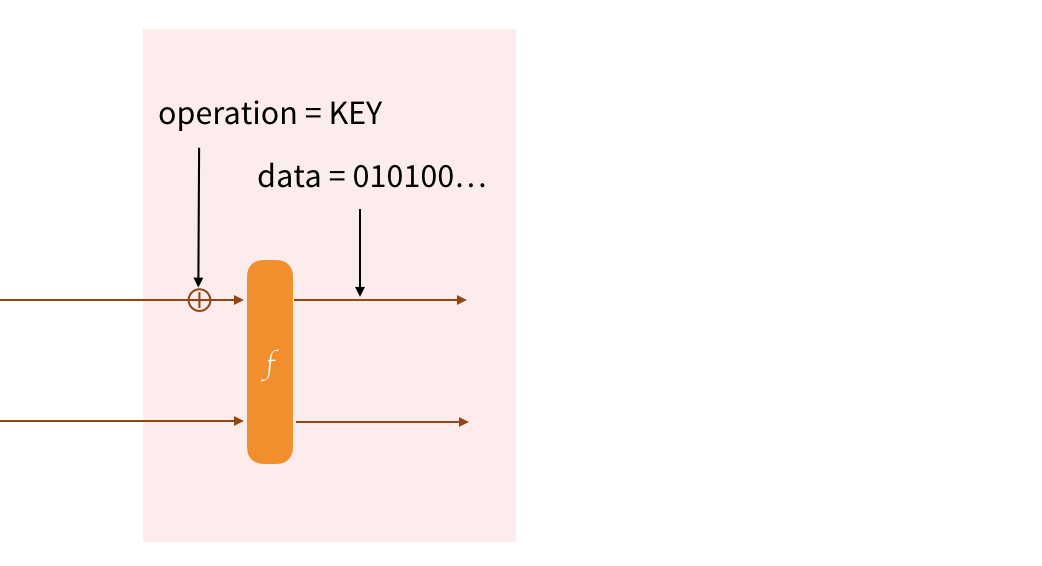
We'll start by keying our protocol. We first absorb the name of the operation (Strobe is verbose). We then permute (via the forceF flag) to start on a fresh block. Since the KEY operation also provides forward-secrecy, the cbefore internal operation is used to replace the bits of the state with the bits of the input (the key).
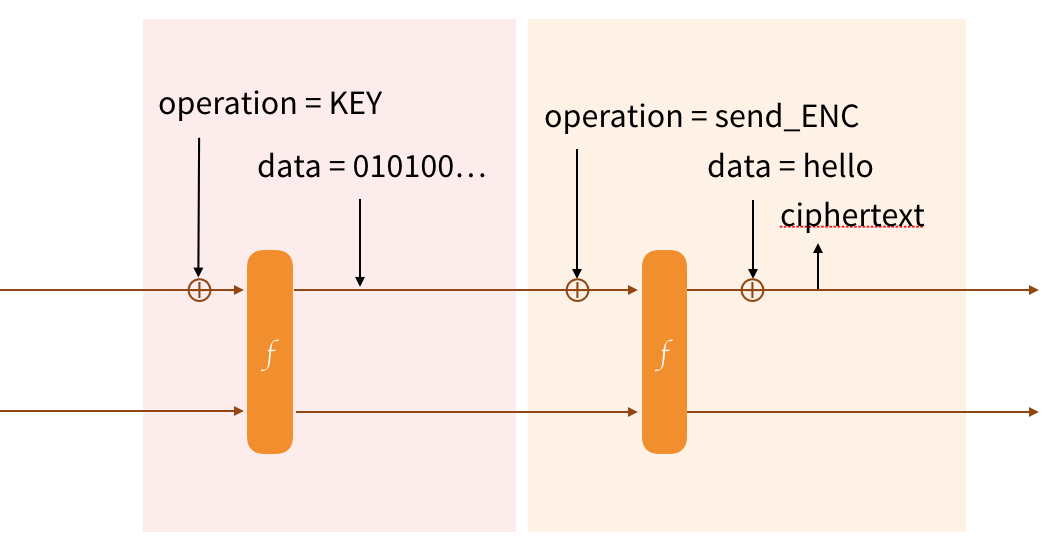
After that we want to encrypt some data. We'll absorb the name of the operation (send_ENC), we'll permute (forceF) and we'll XOR our plaintext with the state to encrypt it. We can then send that ciphertext, which is coincidentally also part of the new state of our duplex construction.
I'll give you two more examples. We can't just send encrypted data like that, we need to protect its integrity. And why not including some additional data that we want to authenticate:
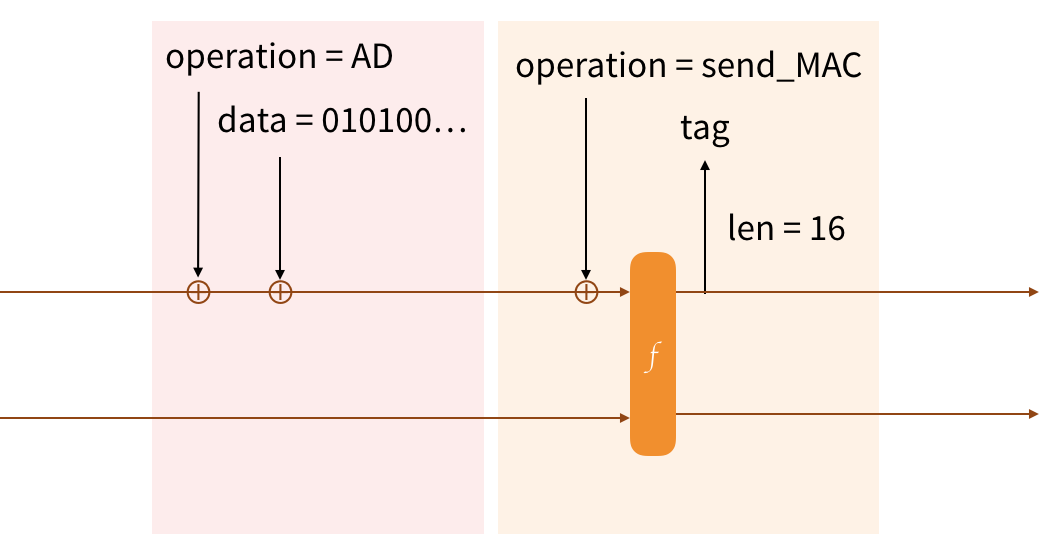
You'll notice, AD does not need to permute the Strobe state, this is because we're not sending anything (or obtaining an output from the construction) so we do not need to depend on what has happened previously yet. For the send_MAC operation we do need that though, and we'll use the cafter internal operation with an input of 16 zeros to obtain the first 16 bytes of the state.
In these description, I've simplified Strobe and omitted the padding. There is also a flag that is differently set depending on who sent the first message. All these details can be learned through the specification.
Now what?
Go play with it! Here is a list of things:
Note that this is still a beta, and it's still experimental.
I was interviewed by Constanze Kurtz for Netzpolitik.org
We talked to the cryptographer David Wong about crypto-related blogs worth reading and exploring in an interview. We also asked him about the changing landscape of the crypto-world and the awareness of IT security issues.
You can read the full interview here.
The list of crypto/security blogs I maintain is available here on Github.