Quick access to articles on this page:
more on the next page...
The wierdness of ==
Do you know what happens when you run this code in PHP?
<?php
var_dump(md5('240610708') == md5('QNKCDZO'));
var_dump(md5('aabg7XSs') == md5('aabC9RqS'));
var_dump(sha1('aaroZmOk') == sha1('aaK1STfY'));
var_dump(sha1('aaO8zKZF') == sha1('aa3OFF9m'));
var_dump('0010e2' == '1e3');
var_dump('0x1234Ab' == '1193131');
var_dump('0xABCdef' == ' 0xABCdef');
?>
Check the answer here. That's right, everything is True.
This is because == doesn't check for type, if a string looks like an integer it will first try to convert it to an integer first and then compare it.
More about PHP == operator here
This is weird and you should use === instead.
Even better, you can use hash_equals (coupled with crypt)
Compares two strings using the same time whether they're equal or not.
This function should be used to mitigate timing attacks; for instance, when testing crypt() password hashes.
Here's the example from php.net:
<?php
$expected = crypt('12345', '$2a$07$usesomesillystringforsalt$');
$correct = crypt('12345', '$2a$07$usesomesillystringforsalt$');
$incorrect = crypt('apple', '$2a$07$usesomesillystringforsalt$');
hash_equals($expected, $correct);
?>
Which will return True.
But why?
the hashed strings start with 0e, for example both strings are equals in php:
md5('240610708') = 0e462097431906509019562988736854
md5('QNKCDZO') = 0e830400451993494058024219903391
because php understands them as both being zero to the power something big. So zero.
Security
Now, if you're comparing unencrypted or unhashed strings and one of them is supposed to be secret, you might have potentialy created the setup for a timing-attack.
Always try to compare hashes instead of the plaintext!
There is a Link section here that is not very visible, I don't really know how I could show its content on the frontpage here. But here's one way:
May 21th
May 22th
May 23th
May 24th
May 25th
May 27th
May 28th
More
And you can find more on the Links section of this blog
To make it short, I did some research on the Boneh and Durfee bound, made some code and it worked. (The bound that allows you to find private keys if they are lesser than \(N^{0.292}\))
I noticed that many times, the lattice was imperfect as many vectors were unhelpful. I figured I could try to remove those and preserve a triangular basis, and I went even further, I removed some helpful vectors when they were annoying. The code is pretty straightforward (compare to the boneh and durfee algorithm here)
So what happens is that I make the lattice smaller, so when I feed it to the lattice reduction algorithm LLL it takes less time, and since the complexity of the whole attack is dominated by LLL, the whole attack takes less time.
It was all just theoric until I had to try the code on the plaid ctf challenge. There I used the normal code and solved it in ~3 minutes. Then I wondered, why not try running the same program but with the research branch?
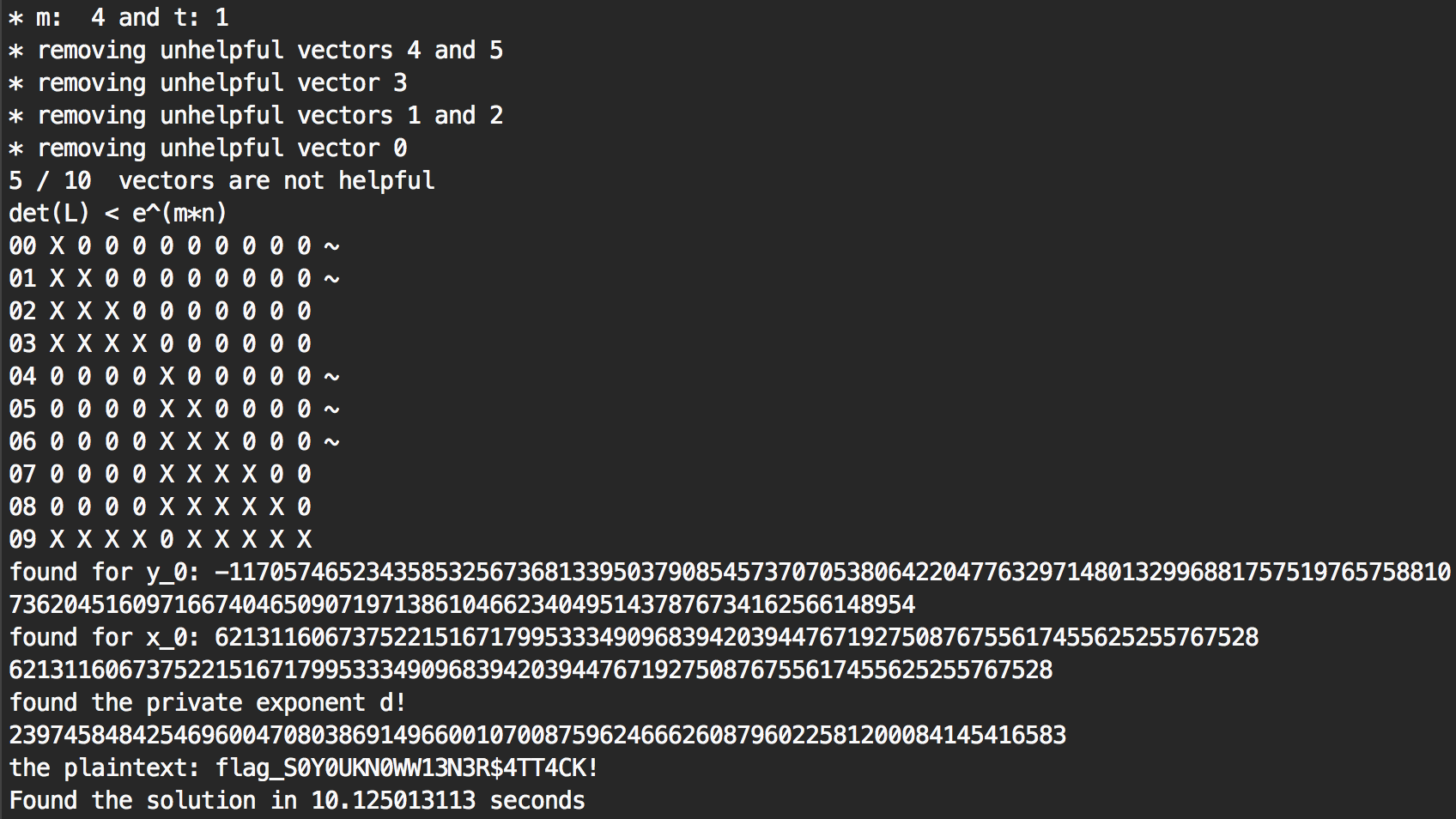
That’s right, only 10 seconds. Because I removed some unhelpful vectors, I could use the value m=4 and it worked. The original algorithm needed m=5 and needed a lattice of dimension 27 when I successfully found a lattice of dimension 10 that worked out. I guess the same thing happened to the 59 triplets before that and that’s why the program ran way faster. 3 minutes to 10 seconds, I think we can call that a success!
The original code:
/!\ this page uses LaTeX, if you do not see this: \( \LaTeX \)
then refresh the page
Plaid CTF
The third crypto challenge of the Plaid CTF was a bunch of RSA triplet \( N : e : c \) with \( N \) the modulus, \( e \) the public exponent and \( c \) the ciphertext.
The public exponents \( e \) are all pretty big, which doesn't mean anything in particular. If you look at RSA's implementation you often see \( 3 \), \( 17 \) or other Fermat primes (\( 2^m + 1 \)) because it speeds up calculations. But such small exponents are not forced on you and it's really up to you to decide how big you want your public exponent to be.
But the hint here is that the public exponents are chosen at random. This is not good. When you choose a public exponent you should be careful, it has to be coprime with \( \varphi(N) \) so that it is invertible (that's why it is always odd) and its related private exponent \( d \) shouldn't be too small.
Maybe one of these public keys are associated to a small private key?
I quickly try my code on a small VM but it takes too much time and I give up.
Wiener
A few days after the CTF is over, I check some write-ups and I see that it was indeed a small private key problem. The funny thing is that they all used Wiener to solve the challenge.
Since Wiener's algorithm is pretty old, it only solves for private exponents \( d < N^{0.25} \). I thought I could give my code a second try but this time using a more powerful machine. I use this implementation of Boneh and Durfee, which is pretty much Wiener's method but with Lattices and it works on higher values of \( d \). That means that if the private key was bigger, these folks would not have found the solution. Boneh and Durfee's method allows to find values of private key up to \( d < N^{0.292} \)!
After running the code (on my new work machine) for 188 seconds (~ 3 minutes) I found the solution :)

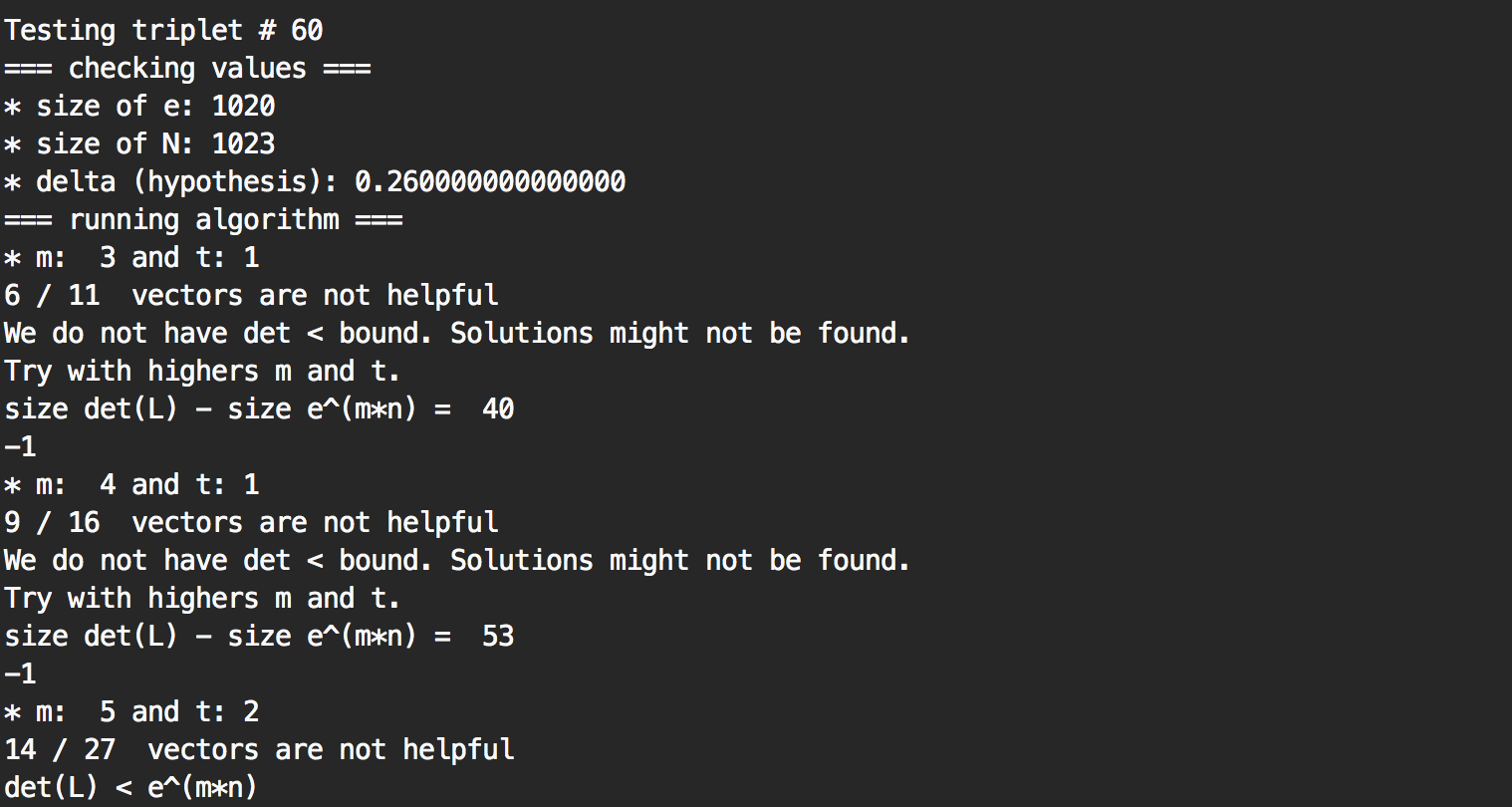
Here we can see that a solution was found at the triplet #60, and that it took several time to figure out the correct size of lattice (the values of \( m \) and \( t \)) so that if there was a private exponent \( d < N^{0.26} \) a solution could be found.
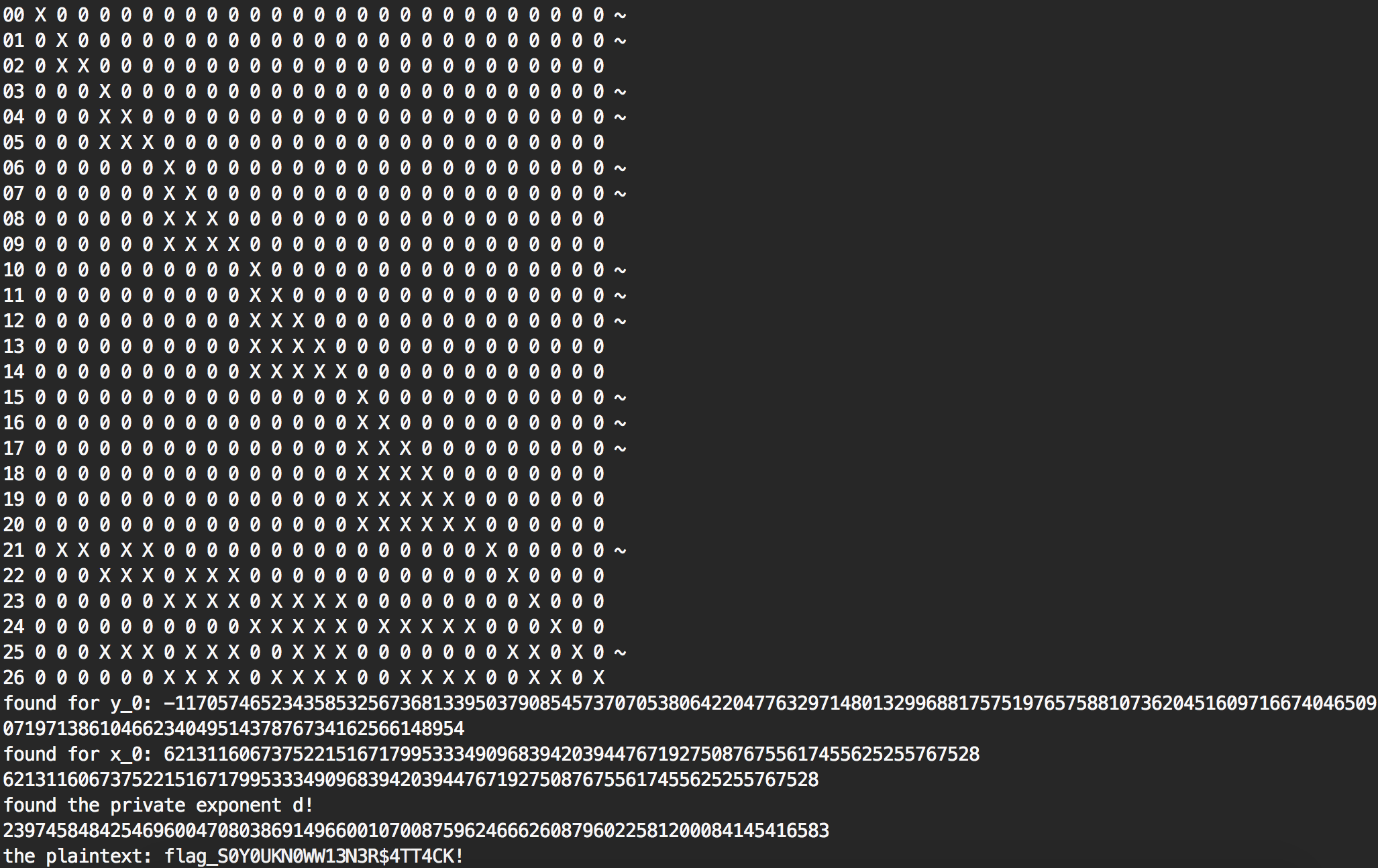
The lattice basis is shown as a matrix (the ~ represents an unhelpful vector, to try getting rid of them you can use the research branch), and the solution is displayed.
Boneh and Durfee
Here is the code if you want to try it. What I did is that I started with an hypothesis \( delta = 0.26 \) which tested for every RSA triplets if there was a private key \( d < N^{0.26 } \). It worked, but if it didn't I would have had to re-run the code for \(delta = 0.27\), \(0.28\), etc...
I setup the problem:
# data is our set of RSA triplets
for index, triplet in enumerate(data):
print "Testing triplet #", index
N = triplet[0]
e = triplet[1]
# Problem put in equation
P.<x,y> = PolynomialRing(ZZ)
A = int((N+1)/2)
pol = 1 + x * (A + y)
I leave the default values and set my hypothesis:
delta = 0.26
X = 2*floor(N^delta)
Y = floor(N^(1/2))
I use strict = true so that if the algorithm will stop if a solution is not sure to be found. Then I increase the values of \( m \) and \( t \) (which increases the size of our lattice) and try again:
solx = -1
m = 2
while solx == -1:
m += 1
t = int((1-2*delta) * m) # optimization from Herrmann and May
print "* m: ", m, "and t:", t
solx, soly = boneh_durfee(pol, e, m, t, X, Y)
If no private key lesser than \(N^{delta}\) exists, I try the next triplet. However, if a solution is found, I stop everything and display it.
Remember our initial equation:
\[ e \cdot d = f(x, y) \]
And what we found are \(x\) and \(y\)
if solx != 0:
d = int(pol(solx, soly) / e)
print "found the private exponent d!"
print d
m = power_mod(triplet[2], d, N)
hex_string = "%x" % m
import binascii
print "the plaintext:", binascii.unhexlify(hex_string)
break
And that's it!
More?
If you don't really know about lattices, I bet it was hard to follow. But do not fear! I made a video explaining the basics and a survey of Coppersmith and Boneh & Durfee
Also go here and click on the follow button.
Plaid, The biggest CTF Team, was organizing a Capture The Flag contest last week. There were two crypto challenges that I found interesting, here is the write-up of the second one:
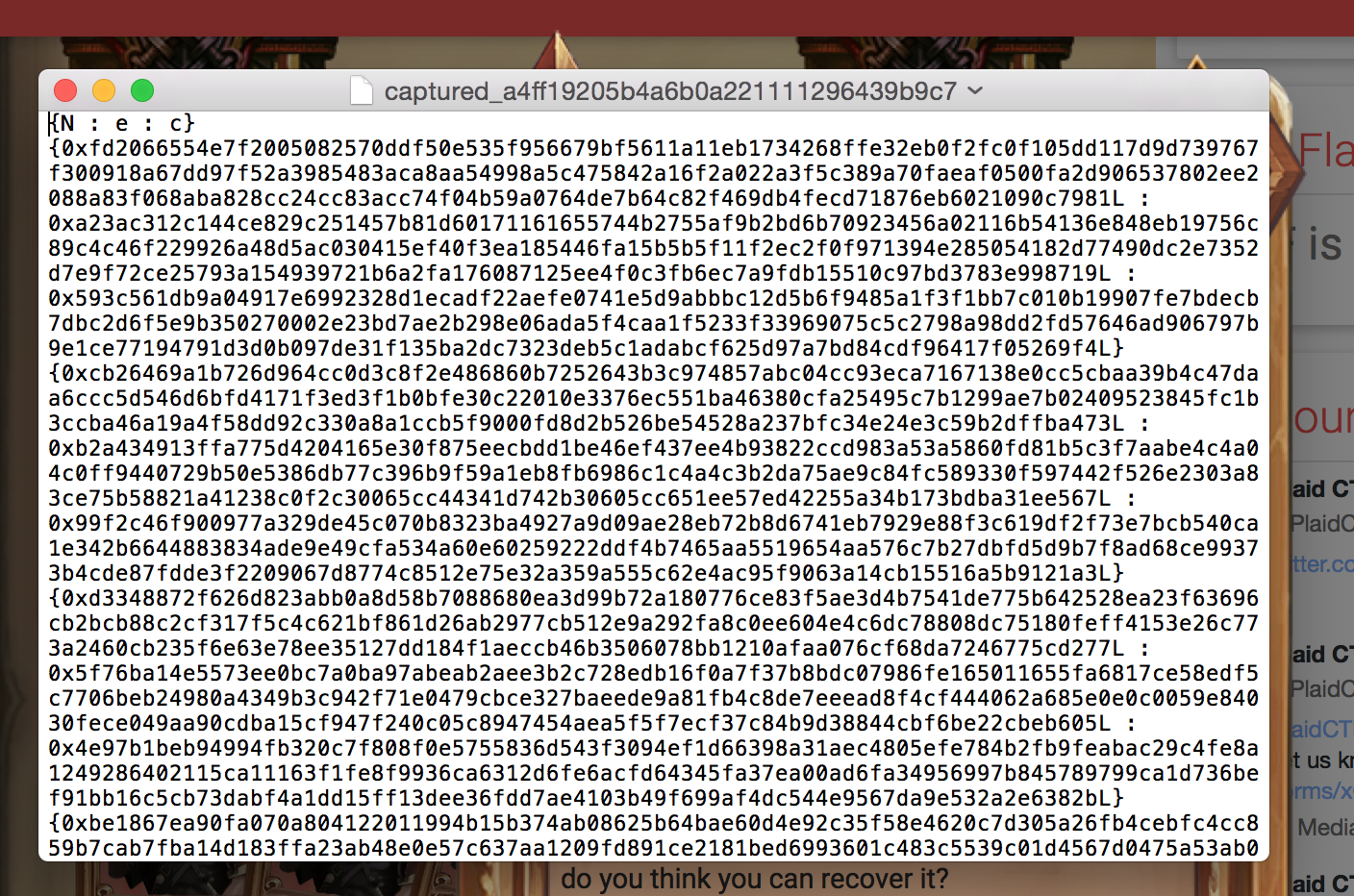
You are given a file with a bunch of triplets:
{N : e : c}
and the hint was that they were all encrypting the same message using RSA. You could also easily see that N was the same modulus everytime.
The trick here is to find two public exponent \( e \) which are coprime: \( gcd(e_1, e_2) = 1 \)
This way, with Bézout's identity you can find \( u \) and \( v \) such that: \(u \cdot e_1 + v \cdot e_2 = 1 \)
So, here's a little sage script to find the right public exponents in the triplets:
for index, triplet in enumerate(truc[:-1]):
for index2, triplet2 in enumerate(truc[index+1:]):
if gcd(triplet[1], triplet2[1]) == 1:
a = index
b = index2
c = xgcd(triplet[1], triplet2[1])
break
Now that have found our \( e_1 \) and \( e_2 \) we can do this:
\[ c_1^{u} * c_2^{v} \pmod{N} \]
And hidden underneath this calculus something interesting should happen:
\[ (m^{e_1})^u * (m^{e_2})^u \pmod{N} \]
\[ = m^{u \cdot e_1 + v \cdot e_2} \pmod{N} \]
\[ = m \pmod{N} \]
And since \( m < N \) we have our solution :)
Here's the code in Sage:
m = Mod(power_mod(e_1, u, N) * power_mod(e_2, v, N), N)
And after the crypto part, we still have to deal with the presentation part:
hex_string = "%x" % m
import binascii
binascii.unhexlify(hex_string)
Tadaaa!! And thanks @spdevlin for pointing me in the right direction :)
The Plaid Parliament of Pwning, a security team at Carnegie Mellon University is organizing a CTF right now until tomorrow: http://play.plaidctf.com/
There are two crypto challenges at the moment, and maybe more if someone unlocks one. Have fun!
RFC
So, RFC means Request For Comments and they are a bunch of text files that describe different protocols. If you want to understand how SSL, TLS (the new SSL) and x509 certificates (the certificates used for SSL and TLS) all work, for example you want to code your own OpenSSL, then you will have to read the corresponding RFC for TLS: rfc5280 for x509 certificates and rfc5246 for the last version of TLS (1.2).

x509
x509 is the name for certificates which are defined for:
informal internet electronic mail, IPsec, and WWW applications
There used to be a version 1, and then a version 2. But now we use the version 3. Reading the corresponding RFC you will be able to read such structures:
Certificate ::= SEQUENCE {
tbsCertificate TBSCertificate,
signatureAlgorithm AlgorithmIdentifier,
signatureValue BIT STRING }
those are ASN.1 structures. This is actually what a certificate should look like, it's a SEQUENCE of objects.
- The first object contains everything of interest that will be signed, that's why we call it a To Be Signed Certificate
- The second object contains the type of signature the CA used to sign this certificate (ex: sha256)
- The last object is not an object, its just some bits that correspond to the signature of the TBSCertificate after it has been encoded with DER
ASN.1
It looks small, but each object has some depth to it.
The TBSCertificate is the biggest one, containing a bunch of information about the client, the CA, the publickey of the client, etc...
TBSCertificate ::= SEQUENCE {
version [0] EXPLICIT Version DEFAULT v1,
serialNumber CertificateSerialNumber,
signature AlgorithmIdentifier,
issuer Name,
validity Validity,
subject Name,
subjectPublicKeyInfo SubjectPublicKeyInfo,
issuerUniqueID [1] IMPLICIT UniqueIdentifier OPTIONAL,
-- If present, version MUST be v2 or v3
subjectUniqueID [2] IMPLICIT UniqueIdentifier OPTIONAL,
-- If present, version MUST be v2 or v3
extensions [3] EXPLICIT Extensions OPTIONAL
-- If present, version MUST be v3
}
DER
A certificate is of course not sent like this. We use DER to encode this in a binary format.
Every fieldname is ignored, meaning that if we don't know how the certificate was formed, it will be impossible for us to understand what each value means.
Every value is encoded as a TLV triplet: [TAG, LENGTH, VALUE]
For example you can check the GITHUB certificate here
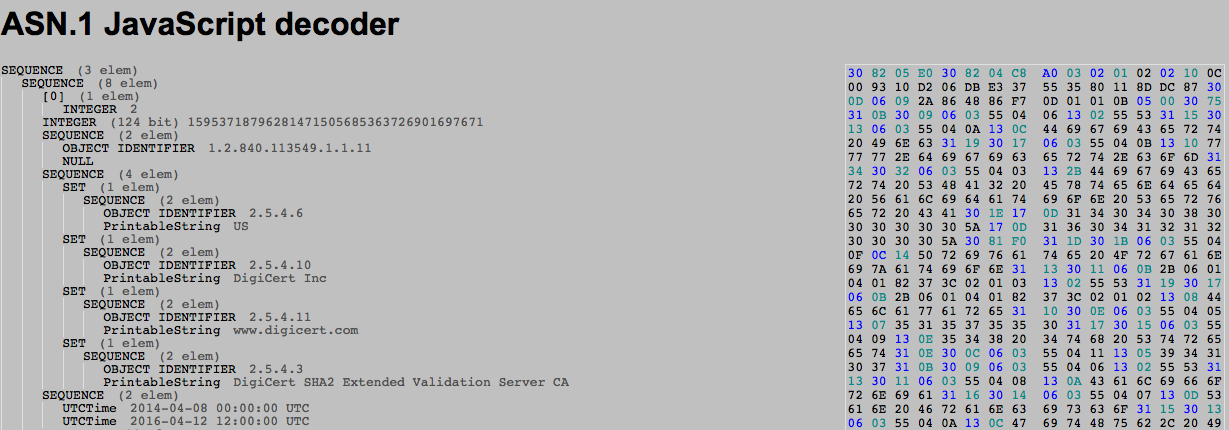
On the right is the hexdump of the DER encoded certificate, on the left is its translation in ASN.1 format.
As you can see, without the RFC near by we don't really know what each value corresponds to. For completeness here's the same certificate parsed by openssl x509 command tool:
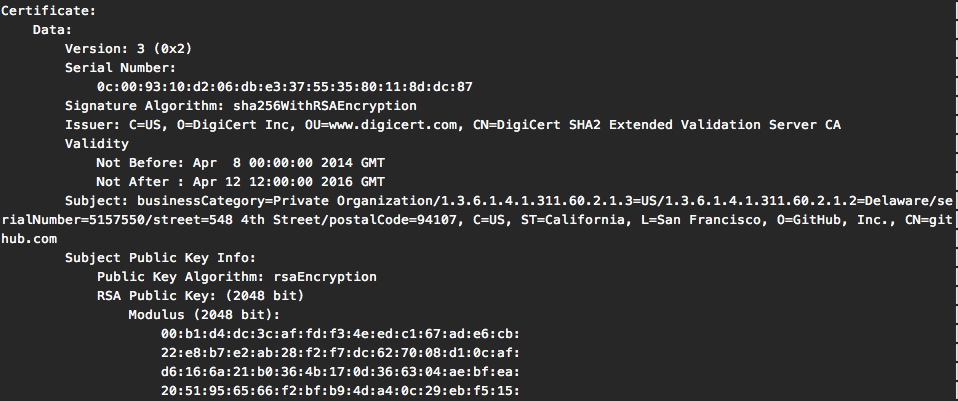
How to read the DER encoded certificate
So go back and check the hexdump of the GITHUB certificate, here is the beginning:
30 82 05 E0 30 82 04 C8 A0 03 02 01 02
As we saw in the RFC for x509 certificates, we start with a SEQUENCE.
Certificate ::= SEQUENCE {
Microsoft made a documentation that explains pretty well how each ASN.1 TAG is encoded in DER, here's the page on SEQUENCE
30 82 05 E0
So 30 means SEQUENCE. Since we have a huge sequence (more than 127 bytes) we can't code the length on the one byte that follows:
If it is more than 127 bytes, bit 7 of the Length field is set to 1 and bits 6 through 0 specify the number of additional bytes used to identify the content length.
(in their documentation the least significant bit on the far right is bit zero)
So the following byte 82, converted in binary: 1000 0010, tells us that the length of the SEQUENCE will be written in the following 2 bytes 05 E0 (1504 bytes)
We can keep reading:
30 82 04 C8 A0 03 02 01 02
Another Sequence embedded in the first one, the TBSCertificate SEQUENCE
TBSCertificate ::= SEQUENCE {
version [0] EXPLICIT Version DEFAULT v1,
The first value should be the version of the certificate:
A0 03
Now this is a different kind of TAG, there are 4 classes of TAGs in ASN.1: UNIVERSAL, APPICATION, PRIVATE, and context-specific. Most of what we use are UNIVERSAL tags, they can be understood by any application that knows ASN.1. The A0 is the [0] (and the following 03 is the length). [0] is a context specific TAG and is used as an index when you have a series of object. The github certificate is a good example of this, because you can see that the next index used is [3] the extensions object:
TBSCertificate ::= SEQUENCE {
version [0] EXPLICIT Version DEFAULT v1,
serialNumber CertificateSerialNumber,
signature AlgorithmIdentifier,
issuer Name,
validity Validity,
subject Name,
subjectPublicKeyInfo SubjectPublicKeyInfo,
issuerUniqueID [1] IMPLICIT UniqueIdentifier OPTIONAL,
-- If present, version MUST be v2 or v3
subjectUniqueID [2] IMPLICIT UniqueIdentifier OPTIONAL,
-- If present, version MUST be v2 or v3
extensions [3] EXPLICIT Extensions OPTIONAL
-- If present, version MUST be v3
}
Since those obects are all optionals, skipping some without properly indexing them would have caused trouble parsing the certificate.
Following next is:
02 01 02
Here's how it reads:
_______ tag: integer
| ____ length: 1 byte
| | _ value: 2
| | |
| | |
v v v
02 01 02
The rest is pretty straight forward except for IOD: Object Identifier.
Object Identifiers
They are basically strings of integers that reads from left to right like a tree.
So in our Github's cert example, we can see the first IOD is 1.2.840.113549.1.1.11 and it is supposed to represent the signature algorithm.
So go to http://www.alvestrand.no/objectid/top.html and click on 1, and then 1.2, and then 1.2.840, etc... until you get down to the latest branch of our tree and you will end up on sha256WithRSAEncryption.
Here's a more detailed explanation on IOD and here's the microsoft doc on how to encode IOD in DER.
Like the audit of OpenSSL wasn't awesome enough, today we learned that we were going to audit Let's Encrypt this summer as well. Pretty exciting agenda for an internship!
https://letsencrypt.org/2015/04/14/ncc-group-audit.html
ISRG has engaged the NCC Group Crypto Services team to perform a security review of Let’s Encrypt’s certificate authority software, boulder, and the ACME protocol. NCC Group’s team was selected due to their strong reputation for cryptography expertise, which brought together Matasano Security, iSEC Partners, and Intrepidus Group.








