Quick access to articles on this page:
more on the next page...
If at some point you realize that doing cryptography means having to manage long-term keys, it means you’re standing in the world of key management.
Makes sense right?
In these lands, you are going to run into scenarios where attackers can be quite close to your applications.
I call these highly-adversarial environments.
Imagine using your credit card on an ATM skimmer (a doodads that a thief can place on top of the card reader of an ATM in order to copy the content of your credit card, see picture bellow); downloading an application on your mobile phone that compromises the OS; hosting a web application in a colocated server shared with a malicious customer; managing highly-sensitive secrets in a data center that gets breached; and so on.

These scenarios suck, and are very counterintuitive to most cryptographers. This is because cryptography has come a long way since the historical “Alice wants to encrypt a message to Bob without Eve intercepting it”. Nowadays, it’s often more like “Alice wants to encrypt a message to Bob, but Alice is also Eve”.
The key here is that in these scenarios, there’s not much that can be done cryptographically (unless you believe in whitebox crypto) and hardware can go a long way to help.
OK, so now we have a whole world of new doohickeys to learn about, and there’s a lot of thingamabob believe me (hence the dense title).
It can be quite confusing to learn about all of this, so here we go: my promise is that by the end of this blogpost series you’ll have a better understanding of what are all these different hardware solutions.
Keep in mind that none of these solutions are pure cryptographic solutions: they are all defense-in-depth (and sometimes dubious) solutions that serve to hide secrets and their associated sensitive cryptographic operations. They also all have a given cost, meaning that if a sophisticated attacker decides to break the bank, there’s not much we can do (besides raising the cost of an attack).
OK let's get started.
Obfuscation
By definition obfuscation has nothing to do with security: it is the act of scrambling something so that it still work but is hard to understand. So for the laugh, let’s first mention whitebox cryptography which attempts to “cryptographically” obfuscate the key inside of an algorithm. That’s right, you have the source code of some AES-based encryption algorithm with a fixed key, and it encrypts and decrypts fine, but the key is mixed so well with the implementation that it is too confusing for anyone to extract the key from the algorithm. That's the theory. Unfortunately in practice, no published whitebox crypto algorithm has been found to be secure, and most commercial solutions are closed-source due to this fact (security through obscurity kinda works in the real world). Again, it’s all about raising the cost and making it harder for attackers.
All in all, whitebox crypto is a big industry that sells dubious products to businesses in need of DRM solutions. On the more serious side, there is a branch of cryptography called Indistinguishability obfuscation (iO) that attempts to do this cryptographically (so for realz). iO is a very theoretical, impractical, and so far not-really-proven field of research. We’ll see how that one goes.
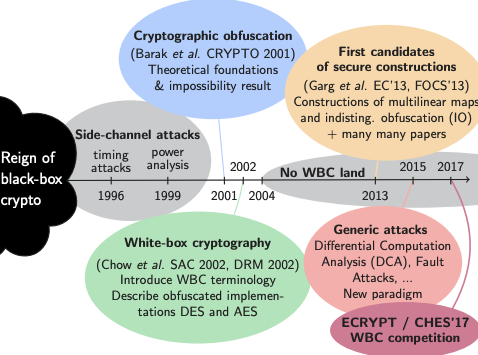
(Timeline of whitebox cryptography, taken from Matthieu Rivain’s slides)
Smart Cards
OK, whitebox crypto is not great, and worse: even if you can’t extract the key, you can still copy the program instead of trying to extract the key (and use it to do whatever cryptographic operation it features). It would be great if we could prevent people from copying secrets from sensitive devices though, or even prevent them from seeing what’s going on when the device performs cryptographic operations.
A smart card is exactly this. It’s what you commonly find in credit cards, and is activated by either inserting it into, or using Near-field Communication (NFC) by getting the smart card close enough to, a payment terminal (also called Point of Sale or PoS terminal).
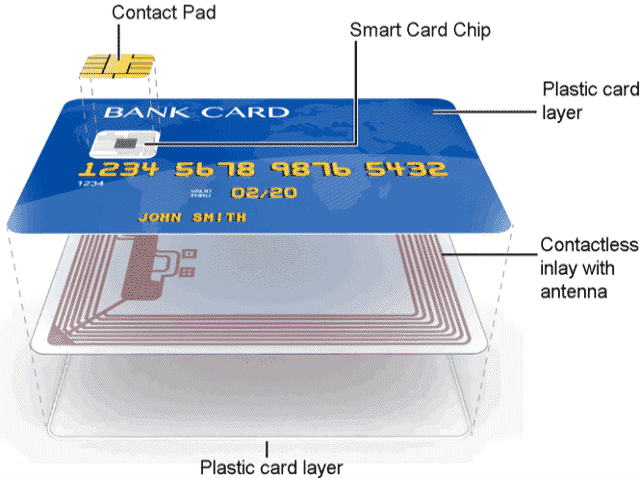
Smart cards are pretty old, and started as a practical way to get everyone a pocket computer. Indeed, a smart cart embarks a CPU, memory (RAM, ROM and EEPROM), input/output, hardware random number generator (so called TRNGs), etc.) unlike the not-so-smart cards that only had data stored in them via a magnetic stripe (which in turn can be easily copied via the skimmers I talked about previously).
Today, it seems like the same people all have a much more powerful computer in their pockets, so smart cards are probably going to die.
(Rob Wood is pointing to me that more than a quarter of the US still doesn’t have a smart phone, so there’s still some time before this prophecy come to fruition.)
Smart cards mix a number of physical and logical techniques to prevent observation, extraction, and modification of its execution environment and some of its memory (where secrets are stored). But as I said earlier, it’s all about how much money you want an attacker to be spending, and there exist many techniques that attempt at breaking these cards:
- Non-invasive attacks such as differential power analysis (DPA) analyze the power consumption of the smart card while it is doing cryptographic operations in order to extract the associated keys.
- Semi-invasive attacks require access to the chip’s surface to mount attacks such as differential fault analysis (DFA) which use heat, lasers, and other techniques to modify the execution of a program running on the smart card in order to leak the key via cryptographic attacks (see my post on RSA signature fault attacks for an example).
- Finally invasive silicon attacks can modify the circuitry in the silicon itself to alter its function and reveal secrets.
Secure Elements
Smart cards got really popular really fast, and it became obvious that having such a secure blackbox in other devices could be useful. The concept of a secure element was born: a tamper-resistant microcontroller that can be found in a pluggable form factor like UUICs (SIM cards required by carriers to access their 3G/4G/5G network) or directly bonded on chips and motherboards like the embedded SE (eSE) attached to an iPhone’s NFC chip. Really just a small separate piece of hardware meant to protect your secrets and their usage in cryptographic operations.
SEs are an evolution of the traditional chip that resides in smart cards, which have been adapted to suit the needs of an increasingly digitalized world, such as smartphones, tablets, set top boxes, wearables, connected cars, and other internet of things (IoT) devices. (GlobalPlatform)
Secure elements are a key concept to protect cryptographic operations in the Internet of Things (IoTs), a colloquial (and overloaded) term to refer to devices that can communicate with other devices (think smart cards in credit cards, SIM cards in phones, biometric data in passports, garage keys, smart home sensors, and so on).
Thus, you can see all of the solutions that will follow in this blogpost series as secure elements implemented in different form factors, using different techniques, and providing different level of defense-in-depth.
If you are required to use a secure element (to store credit card data for example), you also most likely have to get it certified. The main definition and standards around a secure element come from GlobalPlatform, but there exist more standards like Common Criteria (CC), NIST’s FIPS, EMV (for Europay, Mastercard, and Visa), and so on.
If you’re in the market of buying secure microcontrollers, you will often see claims like “FIPS 140-2 certified” and “certified CC EAL 5+” next to it. Claims that can be obtained after spending some quality time, and a lot of money, with licensed certification labs.
Host Card Emulation (HCE)
It’s 2020, most people have a computer in their pocket: a smart phone. What’s the point of a credit card anymore? Well, not much, nowadays more and more payment terminals support contactless payment via the Near-field Communication (NFC) protocol, and more and more smartphones ship with an NFC chip that can potentially act as a credit card.
NFC for payment is specified as Card Emulation. Literally: it emulates a bank card.
Banks allow you to do this only if you have a secure element.
Since Apple has full control over its hardware, it can easily add a secure element to its new iPhones to support payment, and this is what Apple did (with an embedded SE bonded to the NFC chip since the iPhone 6). iPhone users can register a bank card with the Apple wallet application, Apple can then obtain the card’s secrets from the issuing bank, and the card secrets can finally be stored in the eSE. The secure element communicates directly with the NFC chip and then to NFC readers, thus a compromise of the phone OS does not impact the secure element.
Google, on the other hand, had quite a hard time introducing payment to Android-based mobile phones due to phone vendors all doing different things. The saving technology for Google ended up being a cloud-based secure element called Host Card Emulation (HCE) introduced in 2013 in Android 4.4.
How does it work? Google stores your credit card information in a secure element in the cloud (instead of your phone), and only gives your phone access to short-lived single-use PAN (card numbers).
(Note that some Android devices do have an eSE that can be used instead of HCE, and some SIM cards can also be used as secure elements for payment.)
This concept of replacing sensitive long-term information with short-lived tokens is called tokenization.
Sending a random card number that can be linked to your real one is great for privacy: merchants can’t track you as it’ll look like you’re always using a new card number. If your phone gets compromised, the attacker only gets access to a short-lived secret that can only be used for a single payment.
Tokenization is a common concept in security: replace the sensitive data with some random stuff, and have a table secured somewhere safe that maps the random stuff to the real data.
Wikipedia has some cool diagram to show what’s going on whenever you pay with Android Pay or Apple Pay:

Although Apple theoretically doesn't have to use tokenization, since iPhones have secure elements that can store the real PAN, they do use it in order to gain more privacy (it's afterall their new bread and butter).
In part 2 of this blog series I’ll cover HSMs, TPMs, and much more :)
(I would like to thank Rob Wood, Thomas Duboucher, and Lionel Rivière for answering my many questions!)
PS: I'm writing a book which will contain this and much more, check it out!
The coronavirus is shaking the world, on its multiple layers, and cryptography hasn't been spared.
The IACR announced on March 14th that multiple conferences were postponed:
FSE 2020, which was supposed to be held in Athens, Greece, during 22-26 March 2020, has been postponed to 8-12 November 2020.
PKC 2020, which was supposed to be held in Edinburgh, Scotland, during 4-7 May 2020, has been postponed.
EUROCRYPT 2020, which was supposed to be held in Zagreb, Croatia, during 10-14 May 2020, has been postponed.
While some others were not:
No changes have been made at this time to the schedule of CRYPTO 2020, CHES 2020, TCC 2020, and ASIACRYPT 2020, but we will continue to closely monitor the situation and will inform members if changes are needed.
While many workplaces (including mine) are moving to a WFH (work from home) model, will conferences follow?
It seems to be the case at least for Consensus 2020, a cryptocurrency conference organized by coindesk, which is moving to an online model:
Consensus 2020 will now be a completely virtual experience, where attendees from all over the world can participate online at no charge.
On a more dramatic note it seems like several participants of EthCC, which was held in Paris almost a week ago, have contracted the virus. A google spreadsheet has been circulating in order to self-report and figure out who else could have potentially contracted the virus.
Even Vitalik Buterin is rumored to have had mild COVID-19 symptoms. Nobody is out of reach.
On a lighter note, my coworker Kostas presented on proofs of solvency at the lightning talks of Real World Crypto 2020. With his merkle tree-like construction he hopes to make governments accountable when they count the number of people who counted positive to the virus.
The Edwards-curve Digital Signature Algorithm (EdDSA)
You've heard of EdDSA right? The shiny and new signature scheme (well new, it's been here since 2008, wake up).
Since its inception, EdDSA has evolved quite a lot, and some amount of standardization process has happened to it. It's even doomed to be adopted by the NIST in FIPS 186-5!
First, some definition:
- EdDSA stands for Edwards-curve Digital Signature Algorithm. As its name indicates, it is supposed to be used with twisted Edwards curves (a type of elliptic curve). Its name can be deceiving though, as it is not based on the Digital Signature Algorithm (DSA) but on Schnorr signatures!
- Ed25519 is the name given to the algorithm combining EdDSA and the Edwards25519 curve (a curve somewhat equivalent to Curve25519 but discovered later, and much more performant).
EdDSA, Ed25519, and the more secure Ed448 are all specified in RFC 8032.
RFC 8032: Edwards-Curve Digital Signature Algorithm (EdDSA)
RFC 8032 takes some new direction from the original paper:
- It specifies a malleability check during verification, which prevents ill-intentioned people to forge an additional valid signature from an existing signature of yours. Whenever someone talks about Ed25519-IETF, they probably mean "the algorithm with the malleability check".
- It specifies a number of Ed25519 variants, which is the reason of this post.
- Maybe some other stuff I'm missing.
To sign with Ed25519, the original algorithm defined in the paper, here is what you're supposed to do:
- compute the nonce as
HASH(nonce_key || message)
- compute the commitment
R = [nonce]G with G the generator of the group.
- compute the challenge as
HASH(commitment || public_key || message)
- compute the proof
S = nonce + challenge × signing_key
- the signature is
(R, S)
where HASH is just the SHA-512 hash function.
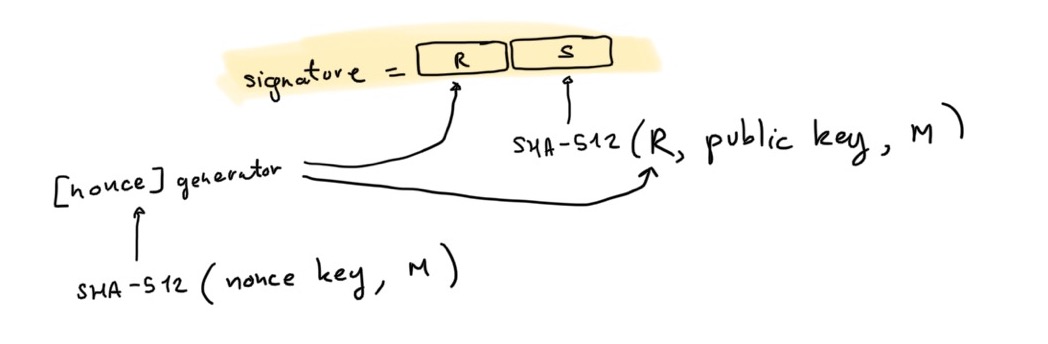
At a high-level this is similar to Schnorr signatures, except for the following differences:
- The nonce is generated deterministically (as opposed to probabilistically) using a fixed
nonce_key (derived from your private key, and the message M. This is one of the cool feature of Ed25519: it prevents you from re-using the same nonce twice.
- The challenge is computed not only with the commitment and the message to sign, but with the public key of the signer as well. Do you know why?
Important: notice that the message here does not need to be hashed before being passed to the algorithm, as it is already hashed as part of the algorithm.
Anyway, we still don't know WTF all the variants specified are.
PureEdDSA, ContextEdDSA and HashEdDSA
Here are the variants that the RFC actually specifies:
- PureEdDSA, shortened as Ed25519 when coupled with Edwards25519.
- HashEdDSA, shortened as Ed25519ph when coupled with Edwards25519 (and where
ph stands for "prehash").
- Something with no name we'll call ContextEdDSA, defined as Ed25519ctx when coupled with Edwards25519.
All three variants can share the same keys. They differ only in their signing and verification algorithms.
By the way Ed448 is a bit different, so from now on I'll focus on EdDSA with the Edwards25519 curve.
Ed25519 (or pureEd25519) is the algorithm I described in the previous section.
Easy!
Ed25519ctx (or ContextEd25519) is pureEd25519 with some additional modification: the HASH(.) function used in the signing protocol I described above is re-defined as HASH(x) = SHA-512(some_encoding(flag, context) || x) where:
flag is set to 0 context is a context string (mandatory only for Ed25519ctx)
In other words, the two instances of hashing in the signing algorithm now include some prefix.
(Intuitively, you can also see that these variants are totally incompatible with each other.)
Right out of the bat, you can see that ContextEd25519 big difference is just that it mandates some domain separation to Ed25519.
Ed25519ph (or HashEd25519), finally, builds on top of ContextEd25519 with the following modifications:
flag is set to 1context is now optional, but advised- the message is replaced with a hash of the message (the specification says that the hash has to be SHA-512, but I'm guessing that it can be anything in reality)
OK. So the big difference now seems that we are doubly-hashing.
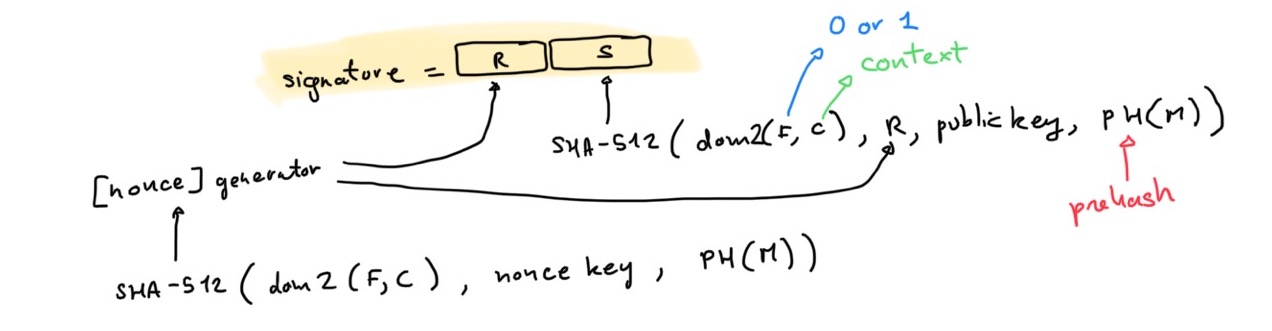
Why HashEdDSA and why double hashing?
First, pre-hashing sucks, this is because it kills the collision resistance of the signature algorithm.
In PureEdDSA we assume that we take the original message and not a hash.
(Although this is not always true, the caller of the function can do whatever they want.)
Then a collision on the hash function wouldn't matter (to make you create a signature that validates two different messages) because you would have to find a collision on the nonce which is computed using a secret (the nonce key).
But if you pre-hash the message, then finding a collision there is enough to obtain a signature that validates two messages.
Thus, you should use PureEdDSA if possible. And use it correctly (pass it the correct message.)
Why is HashEdDSA a thing then?
The EdDSA for more curves paper which was the first to introduce the algorithm has this to say:
The main motivation for HashEdDSA is the following storage issue (which is irrelevant to most well-designed signature applications). Computing the PureEdDSA signature of M requires reading through M twice from a buffer as long as M, and therefore does not support a small-memory “InitUpdate-Final” interface for long messages. Every common hash function H0 supports a smallmemory “Init-Update-Final” interface for long messages, so H0 -EdDSA signing also supports a small-memory “Init-Update-Final” interface for long messages. Beware, however, that analogous streaming of verification for long messages means that verifiers pass along forged packets from attackers, so it is safest for protocol designers to split long messages into short messages to be signed; this splitting also eliminates the storage issue.
Why am I even looking at this rabbit hole?
Because I'm writing a book, and it'd be nice to explain what the hell is going on with Ed25519.

I've been writing about cryptography for a book for a year now, and it has brought me some interesting challenges.
One of them is that I constantly have to throw away what I've learned a long time ago, and imagine what it feels like not to know about a concept.
For example what are key exchanges?
The most intuitive explanation that I knew of (up until recently) was the one given by the wikipedia page on key exchanges.
You might already know about it (unless you're reading this post to learn about key exchanges).
It's a picture that involves paint. Take a look at it, but don't try to understand what is going on if you don't know about key exchanges yet. You can come back to it later.
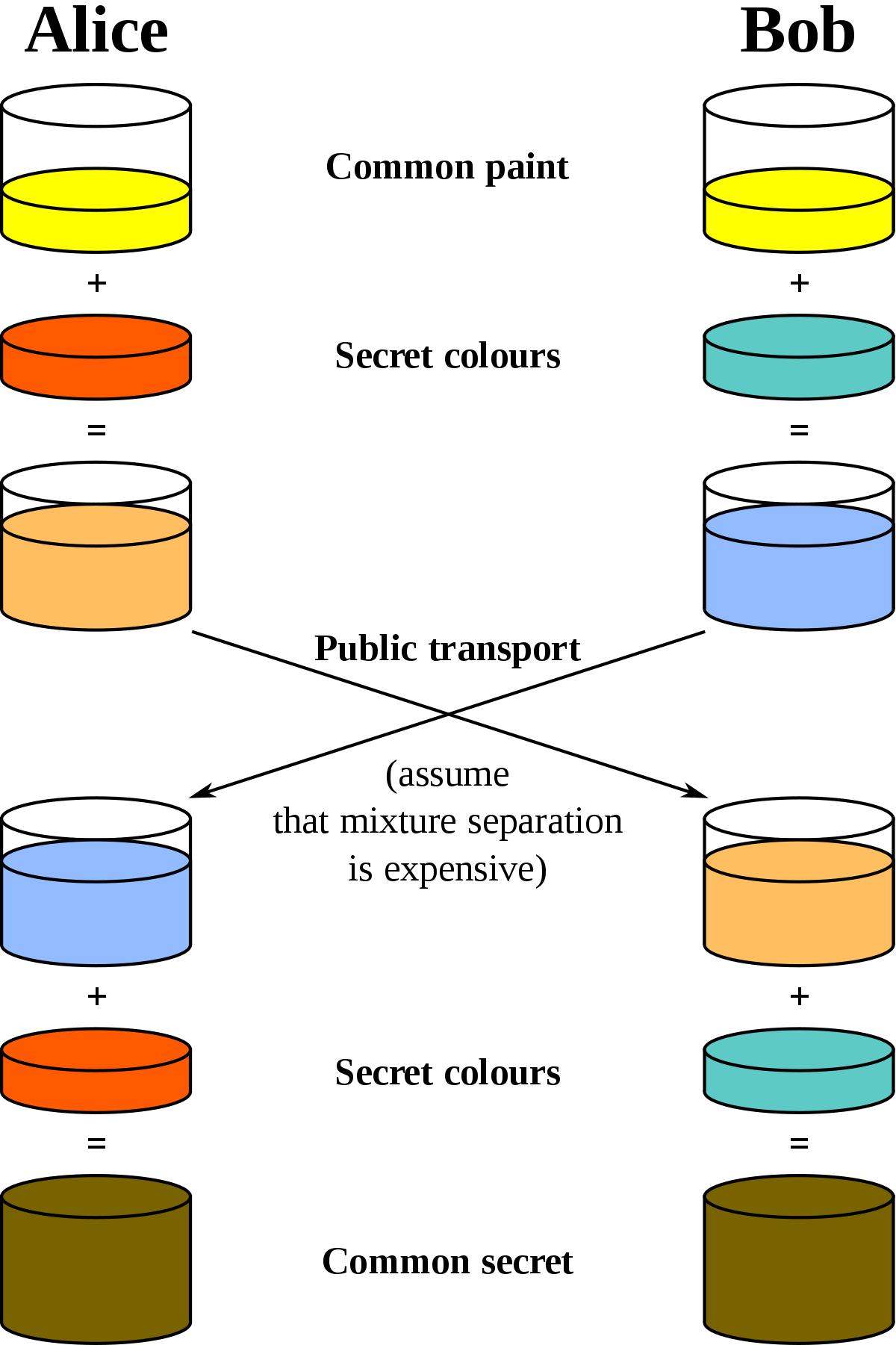
I thought this was great. At least until I tried to explain key exchanges to my friends using this analogy. Nobody got it.
Nobody.
The other problem was that I couldn't use colors to explain anything in my book, as it'll be printed in black & white.
So I sat on the sad realization that I didn't have a great explanation for key exchanges, this for a number of months, and that until a more intuitive idea came to my mind.

The idea goes like this. Imagine that Alice and Bob wants to share a secret, but are afraid that someone is intercepting their communications.
What they do is that they go to the store and buy the same bottle of generic soda.
Once home, they both start a random timer and shake their respective bottles until their timer end.
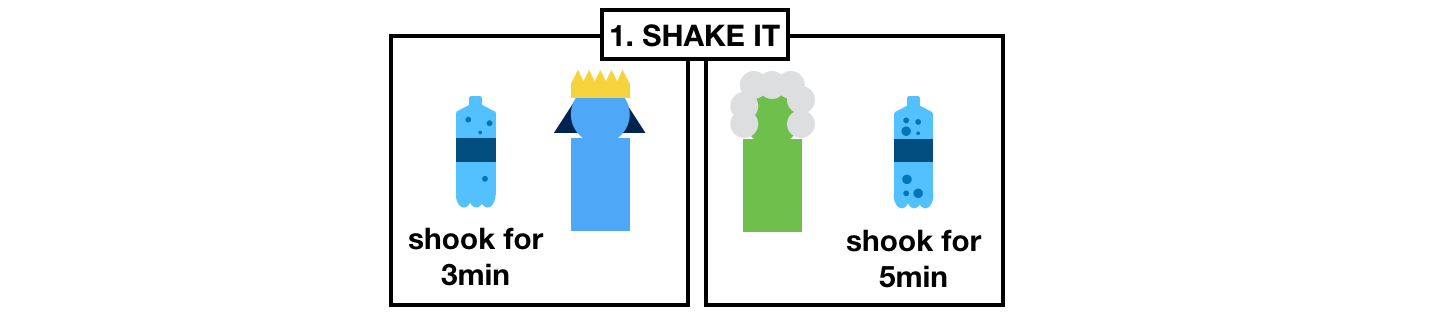
What they obtain are some shaked, pressurized, ready to gush out bottles of sodas.
Each of the bottles will release a different amount of pressure.
After that, they swap bottles. Now Alice has the bottle of Bob, and Bob has Alice's bottle.
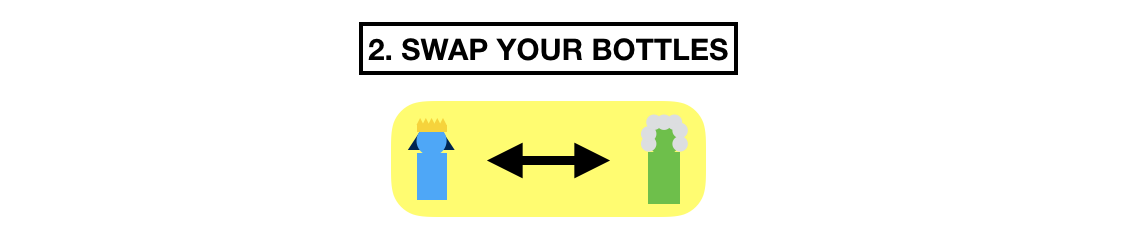
What do they do now? They restart their timers and shake the other person's bottle for the same amount of time.
Shake shake shake!
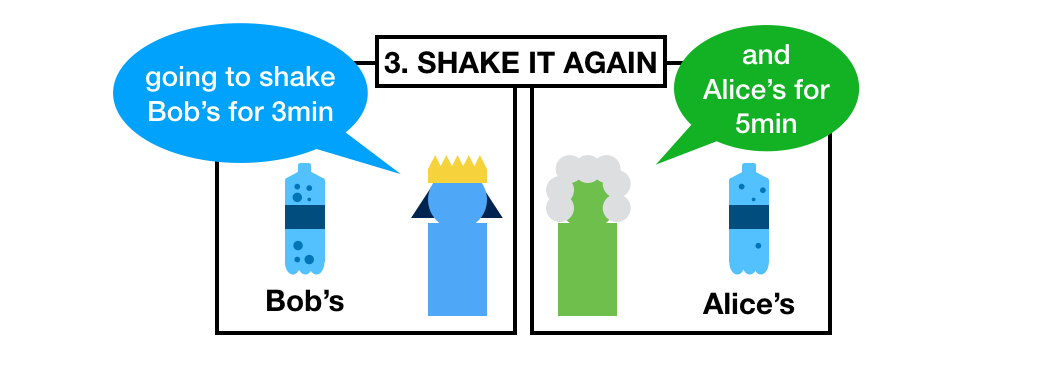
What do they finally obtain? Try to guess.
If I did my job correctly, then I gave you an intuition of how key exchanges work.
Both Alice and Bob should now have two bottle of sodas that will release the same pressure once opened.
And that's the secret!
And even if I steal the two bottles, I can't get a bottle that combines both bottles' pressure.
I recap the whole flow in the picture below:
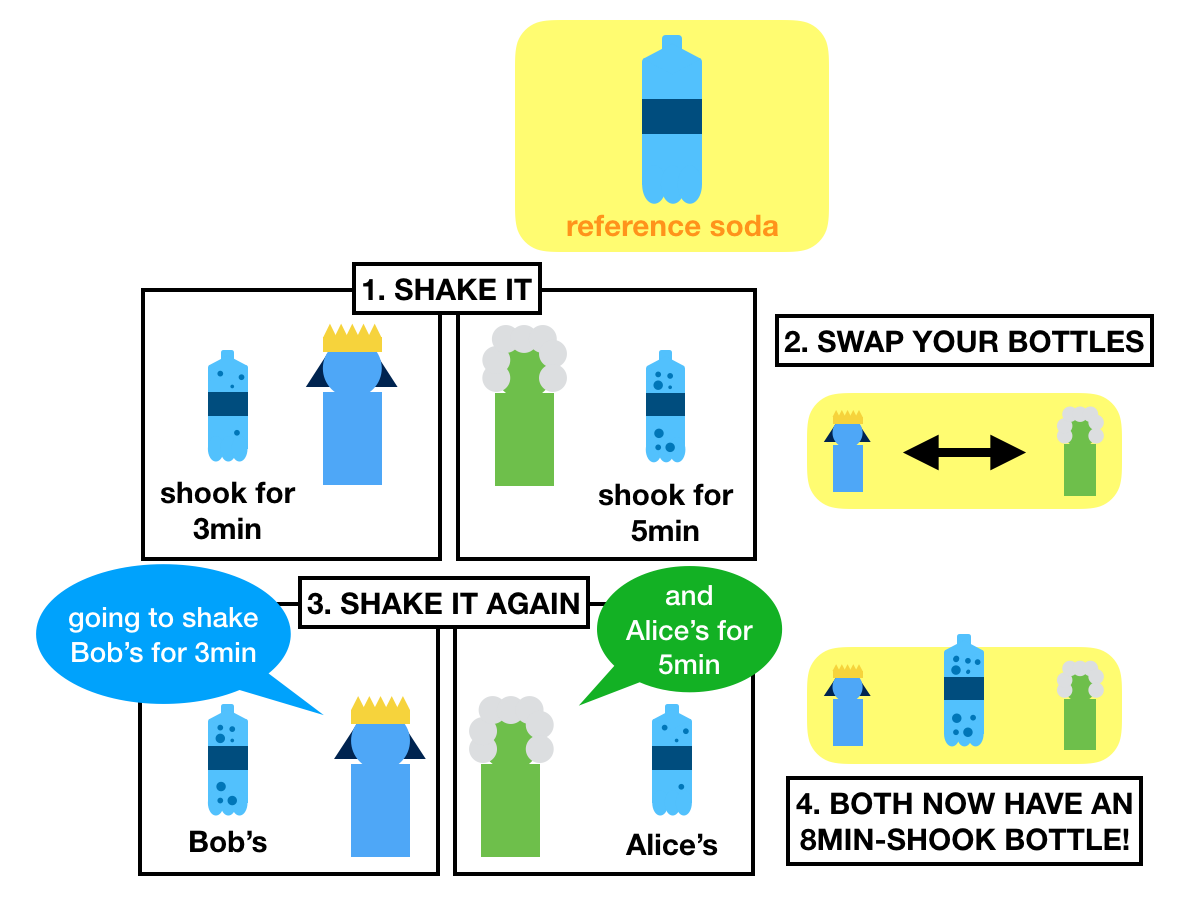
Did you know about key exchanges before? Did you get it? Or did you think the painting example made more sense?
Please tell me in the comment!
This is probably what I'll include in my book as an introduction of what key exchanges are, unless I find a better way to explain it :)
The Let's Encrypt Accident
On August 11th, 2015, Andrew Ayer posted the following email to the IETF mailing list:
I recently reviewed draft-barnes-acme-04 and found vulnerabilities in the DNS, DVSNI, and Simple HTTP challenges that would allow an attacker to fraudulently complete these challenges.
(The author has since then written a more complete explanation of the attack.)
The draft-barnes-acme-04 mentioned by Andrew Ayer is a document specifying ACME, one of the protocols behind the Let's Encrypt Certificate Authority. The thing that your browser trust and that signs the public keys of websites you visit.
The attack was found merely 6 weeks before major browsers were supposed to ship with Let's Encrypt's public keys in their trust store. The draft has since become RFC 8555: Automatic Certificate Management Environment (ACME), mitigating the issues. Since then no cryptographic attacks are known on the protocol.
But how did we get there? What's the deal with signature schemes these days? and are all of our protocols doomed? This is what this blog post will answer.
Let's Encrypt Use Of Signatures
Let's Encrypt is a pretty big deal. Created in 2014, it is a certificate authority ran as a non-profit, and currently providing trust to ~200 million of websites.
(You can read my article Let's Encrypt Overview to learn more about it.)
The key to Let's Encrypt's success are two folds:
- It is free. Before Let's Encrypt most certificate authorities charged fees from webmasters who wanted to obtain certificates.
- It is automated. If you follow their standardized protocol, you can request, renew and even revoke certificates via an API. Contrast that to other certificate authorities who did most processing manually, and took time to issue certificates.
If a webmaster wants her website example.com to provide a secure connection to her users (via HTTPS), she can request a certificate from Let's Encrypt, and after proving that she owns the domain example.com and getting her certificate issued, she will be able to use it to negotiate a secure connection with any browser trusting Let's Encrypt.
That's the theory.
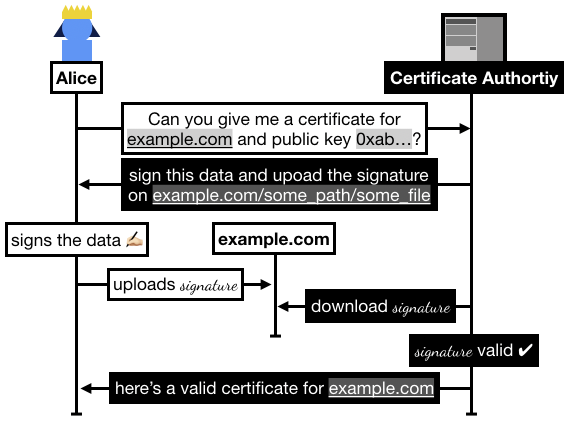
In practice the flow is the following:
- Alice registers on Let's Encrypt with an RSA public key.
- Alice asks Let's Encrypt for a certificate for
example.com.
- Let's Encrypt asks Alice to prove that she owns
example.com, for this she has to sign some data and upload it to example.com/.well-known/acme-challenge/some_file.
- Once Alice has signed and uploaded the signature, she asks Let's Encrypt to go check it.
- Let's Encrypt checks if it can access the file on
example.com, if it successfully downloaded the signature and the signature is valid then Let's Encrypt issues a certificate to Alice.
I recapitulate some of this flow in the following figure:
Now, you might be wondering, what if Alice does not own example.com and manage to man-in-the-middle Let's Encrypt in step 5? That's a real issue that's been bothering me ever since Let's Encrypt launched, and turns out a team of researchers at Princeton demonstrated exactly this in Bamboozling Certificate Authorities with BGP:
We perform the first real-world demonstration of BGP attacks to obtain bogus certificates from top CAs in an ethical manner. To assess the vulnerability of the PKI, we collect a dataset of 1.8 million certificates and find that an adversary would be capable of gaining a bogus certificate for the vast majority of domains
The paper continues and proposes two solutions to sort of remediate, or at least reduce the risk of these attacks:
Finally, we propose and evaluate two countermeasures to secure the PKI: 1) CAs verifying domains from multiple vantage points to make it harder to launch a successful attack, and 2) a BGP monitoring system for CAs to detect suspicious BGP routes and delay certificate issuance to give network operators time to react to BGP attacks.
Recently Let's Encrypt implemented the first solution multi-perspective domain validation, which changes the way step 5 of the above flow is performed: now Let's Encrypt downloads the proof from example.com from multiple places.
How Did The Let's Encrypt Attack Worked
But let's get back to what I was talking about, the attack that Andrew Ayer found in 2015.
In it, Andrew proposes a way to gain control of a Let's Encrypt account that has already validated a domain (let's say example.com)
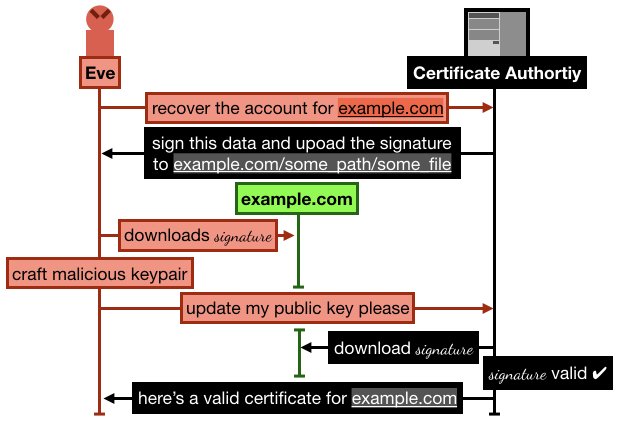
The attack goes like this:
- Alice registers and goes through the process of verifying her domain
example.com by uploading some signature over some data on example.com/.well-known/acme-challenge/some_file. She then successfully manages to obtain a certificate from Let's Encrypt.
- Later, Eve signs up to Let's Encrypt with a new account and new RSA public key, and request to recover the
example.com domain
- Let's Encrypt asks Eve to sign some new data, and upload it to
example.com/.well-known/acme-challenge/some_file (note that the file is still lingering there from Alice's previous domain validation)
- Eve crafts a new malicious keypair, and updates her public key on Let's Encrypt. She then asks Let's Encrypt to check the signature
- Let's Encrypt obtains the signature file from
example.com, the signature matches, Eve is granted ownership of the domain example.com.
I recapitulate the attack in the following figure:
Wait what?
What happened there?
Key Substitution Attack With RSA
In the above attack Eve managed to create a valid public key that validates a given signature and message.
This is because, as Andrew Ayer wrote:
A digital signature does not uniquely identify a key or a message
If you remember how RSA works, this is actually not too hard to understand.

For a fixed signature and (PKCS#1 v1.5 padded) message, a public key (e, N) must satisfy the following equation to validate the signature:
\(\text{signature} = \text{message}^e \pmod{N}\)
One can easily craft a public key that will (most of the time) satisfy the equation:
- \(e = 1\)
- \(N = \text{signature} - \text{message}\)
You can easily verify that the validation works:
$$
\begin{align}
&\text{signature} = \text{message}^e \pmod{N}\\
\iff&\text{signature} = \text{message} \pmod{\text{signature} - \text{message}}\\
\iff&\text{signature} - \text{message} = 0 \pmod{\text{signature} - \text{message}}
\end{align}
$$
By definition the last line is true.
Security of Cryptographic Signatures
Is this issue surprising?
It should be.
And if so why?
This is because of the gap that exists between the theoretical world and the applied world, between the security proofs and the implemented protocol.
Signatures in cryptography are usually analyzed with the EUF-CMA model, which stands for Existential Unforgeability under Adaptive Chosen Message Attack.
In this model YOU generated a key pair, and then I request YOU to sign a number of arbitrary messages. While I observe the signatures you produce, I win if I can at some point in time produce a valid signature over a message I hadn't requested.
Unfortunately, even though our modern signature schemes seem to pass the EUF-CMA test fine, they tend to exhibit some surprising properties.
Subtle Behaviors of Signature Schemes
The excellent paper Seems Legit: Automated Analysis of Subtle Attacks on Protocols that Use Signatures by Dennis Jackson, Cas Cremers, Katriel Cohn-Gordon, and Ralf Sasse attempts to list these surprising properties and the signature schemes affected by them (and then find a bunch of these in protocols using formal verification, it's a cool paper read it).

Let me briefly describe each properties:
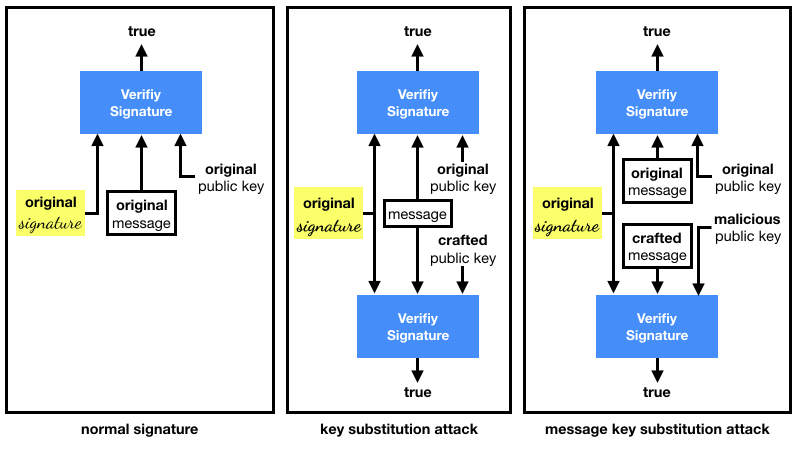
Conservative Exclusive Ownership (CEO)/Destructive Exclusive Ownership (DEO). This refers to what Koblitz and Menezes used to call Duplicate Signature Key Selection (DSKS). In total honesty, I don't think any of these terms are self-explanatory. I find these attacks easier to remember if thought of as the following two variants:
- key substitution attacks (CEO), where a different keypair or public key is used to validate a given signature over a given message.
- message key substitution attacks (DEO), where a different keypair or public key is used to validate given signature over a new message.
To recap: the first attack fixes both the message and the signature, the second one only fixes the signature.
Malleability. Most signature schemes are malleable, meaning that if you give me a valid signature I can tamper with it so that it becomes a different but still valid signature. Note that if I'm the signer I can usually create different signatures for the same message, but here malleability refers to the fact that someone who has zero knowledge of the private key can also create a new valid signature for the same signed message. It is not clear if this has any impact on any real world protocol, eventhough the bitcoin MtGox exchange blamed their loss of funds on this one. From the paper Bitcoin Transaction Malleability and MtGox:
In February 2014 MtGox, once the largest Bitcoin exchange, closed and filed for bankruptcy claiming that attackers used malleability attacks to drain its accounts.
Note that a newer security model called SUF-CMA (for strong EUF-CMA) attempts to include this behavior in the security definition of signature schemes, and some recent standards (like RFC 8032 that specifies Ed25519) are mitigating malleability attacks on their signature schemes.
Re-signability. This one is simple to explain. To validate a signature over message you often don't need the message itself but its digest. This would allow anyone to re-sign the message with their own keys without knowing the message itself. How is this impactful in real world protocols? Not sure, but we never know.
Collidability. This is another not-so-clear if it'll bite you one day: some schemes allow you to craft signatures that will validate under several messages. Worse, Ed25519 as designed allows one to craft a public key and a signature that would validate any message with high probability. (This has been fixed in some implementations like libsodium.)
I recapitulate the substitution attacks in the diagram below:
What to do with all of this information?
Well, for one signature schemes are definitely not broken, and you probably shouldn't worry if your use of them are mainstream.
But if you're designing cryptographic protocols, or if you're implementing something that's more complicated than the every day use of cryptography you might want to keep these in the back of your mind.
 Did you like this content? This is part of a book about how to apply modern cryptography in real world applications. Check it out!
Did you like this content? This is part of a book about how to apply modern cryptography in real world applications. Check it out!
(part 1 is here)
Writing about real world cryptography, it seems like what I end up writing a lot about is protocols and how they solve origin/identity authentication.
Don't get me wrong, confidentiality has interesting problems to (e.g. how to bring confidentiality to a blockchain), but authentication is most of what applied cryptography is about, for realz.
Do I need to convince you?
If you think about it, most protocols are about finding ways to provide authentication to different scenarios. And that's why they can get complicated!
I'll take my life for example, here is the authentication problems and solutions that I use:
- insecure → one-side authenticated. Every day I use HTTPS, which uses the web public-key infrastructure (web PKI) to allow my browser to authenticate any websites on the web. It's a mess, but that's how you scale machine-to-machine authentication nowadays.
- one-side authenticated → mutually-authenticated. Whenever I log into a website, over a secure HTTPS connection, this is what happens. A machine asks me to present some password (in clear, or oblivious via an asymmetric password-authenticated key exchange), or maybe a one-time password (via TOTP), or maybe I'll have to press my thumb on a yubikey (FIDO 2), or maybe I'll have to do a combination of several things (MFA). These are usually machine authenticating humans-type of flow.
- insecure → mutually-authenticated. Whenever I talk to someone on Signal, or connect to a new WiFi, or pair a bluetooth device (like my phone with a car), I go from an insecure connection to a mutually-authenticated connection. There is a bit more nuance here, as sometimes I'll authenticate a machine (a WiFi access point for example) and sometimes I'll authenticate a human (end-to-end encryption). So different techniques work best depending on the type of peer you're trying to talk to.
In the end, I think these are the main three big categories of origin authentication.
Can you think of a better classification?
There is a whole field of authentication in cryptography that is often under-discussed (at least in my opinion).
See, we often like to talk about how key exchanges can also be authenticated, by mean of public-key infrastructures (e.g. HTTPS) or by pre-exchanging secrets (e.g. my previous post on sPAKE), but we seldom talk about post-handshake authentication.
Post-handshake authentication is the idea that you can connect to something (often a hardware device) insecurely, and then "augment" the connection via some information provided in a special out-of-band channel.
But enough blabla, let me give you a real-world example: you link your phone with your car and are then asked to compare a few digits (this pairing method is called "numeric comparison" in the bluetooth spec). Here:
- Out-of-band channel. you are in your car, looking at your screen, this is your out-of-band channel. It provides integrity (you know you can trust the numbers displayed on the screen) but do not necessarily provide confidentiality (someone could look at the screen through your window).
- Short authenticated string (SAS). The same digits displayed on the car's screen and on your phone are the SAS! If they match you know that the connection is secure.
This SAS thing is extremely practical and usable, as it works without having to provision devices with long secrets, or having the user compare long strings of unintelligible characters.
How to do this? You're probably thinking "easy!". An indeed it seems like we could just do a key exchange, and then pass the output in some KDF to create this SAS.
NOPE.
This has been discussed long-and-large on the internet: with key exchange protocols like X25519 it doesn't work.
The reason is that X25519 does not have contributory behavior: I can send you a public key that will lead to a predictable shared secret. In other words: your public key does not contribute (or very little) to the output of the algorithm.
The correct™ solution here is to give more than just the key exchange output to your KDF: give it your protocol transcript. All the messages sent and received. This puts any man-in-the-middle attempts in the protocol to a stop. (And the lesson is that you shouldn't naively customize a key exchange protocol, it can lead to real world failures.)
The next question is, what's more to SAS-based protocols? After all, Sylvain Pasini wrote a 300-page thesis on the subject. I'll answer that in my next post.
have you heard of sPAKE (or bPAKE)?
a sPAKE is first and foremost a PAKE, which stands for Password-Authenticated Key Exchange.
This simply means that authentication in the key exchange is provided via the knowledge of a password.
The s (resp. b) in front means symmetric (resp. balanced). This indicates that both sides know the password.

Other PAKEs where only one side knows the password exist, these are called aPAKE for asymmetric (or augmented) PAKEs.
Yes I know the nomenclature is a bit confusing :)
The most promising sPAKE scheme currently seems to be SPAKE2, which is in the process of being standardized here.
There are other sPAKEs, like Dragonfly which is used in WPA3, but they don't seem to provide as strong properties as SPAKE2.
The trick to a symmetric PAKE is to use the password to blind the key exchange's ephemeral keypairs.
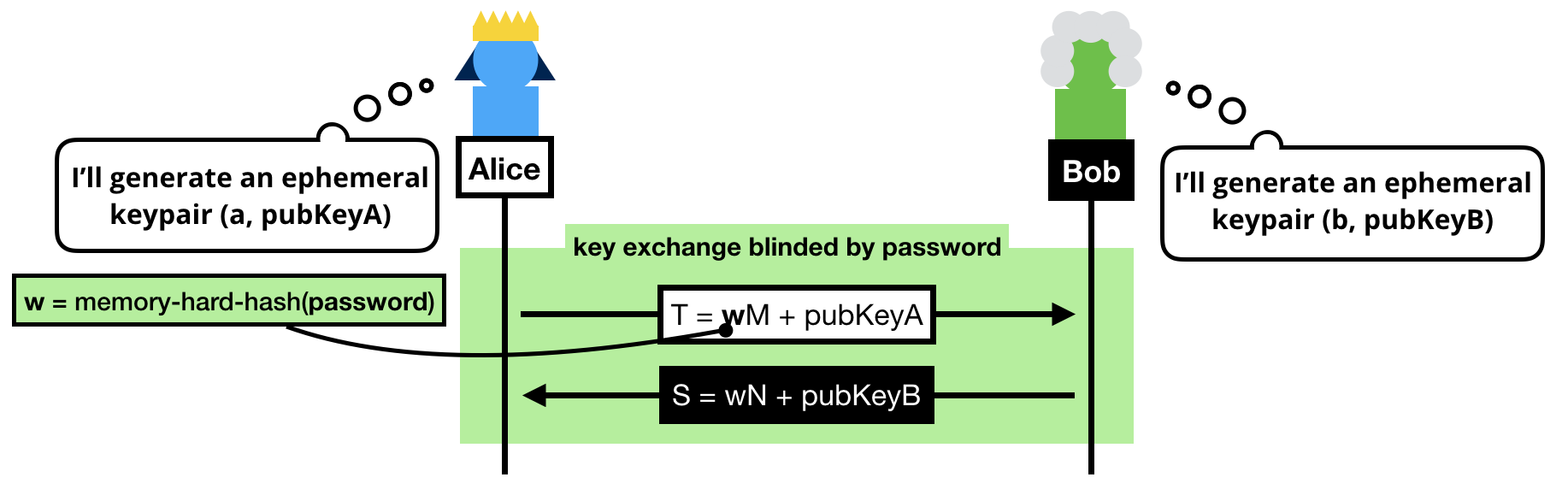
Note that we can't use the password as is, instead we:
- Pass the password into a memory-hard hash function like Argon2 to obtain
w. Can you guess why we do this? (leave a comment if you do!)
- Convert it to a group element. To do this we simply consider
w a scalar and do a scalar multiplication with a generator of our subgroup (M or N depending if you're the client or the server, can you guess why we use different generators?)
NOTE: If you know BLS or OPAQUE, you might be wondering why we don't use a "hash-to-curve" algorithm, this is because we don't need to obtain a group element with an unknown discrete logarithm in SPAKE2.
Once the blinded (with the password) public keys have been exchanged, both sides can compute a shared group element:
- Alice computes
K = h × alice_private_key × (S - w × N)
- Bob computes
K = h × bob_private_key × (T - w × M)
Spend a bit of your time to understand these equations.
What happens is that both Alice and Bob first unblind the public key they've received, then perform a key exchange with it, then multiply it with the value h. What's this value h? The cofactor, or simply put: the other annoying subgroup.
Finally Alice and Bob hash the whole transcript, which is the concatenation of:
- Alice's identity.
- Bob's identity.
- The message Bob sent
S.
- The message Alice sent
T.
- The shared group element
K.
- The hardened password
w.
The hash of this transcript gives us two things:
- A shared secret !
- A key that is further expanded (via a KDF) to obtain two authentication keys.
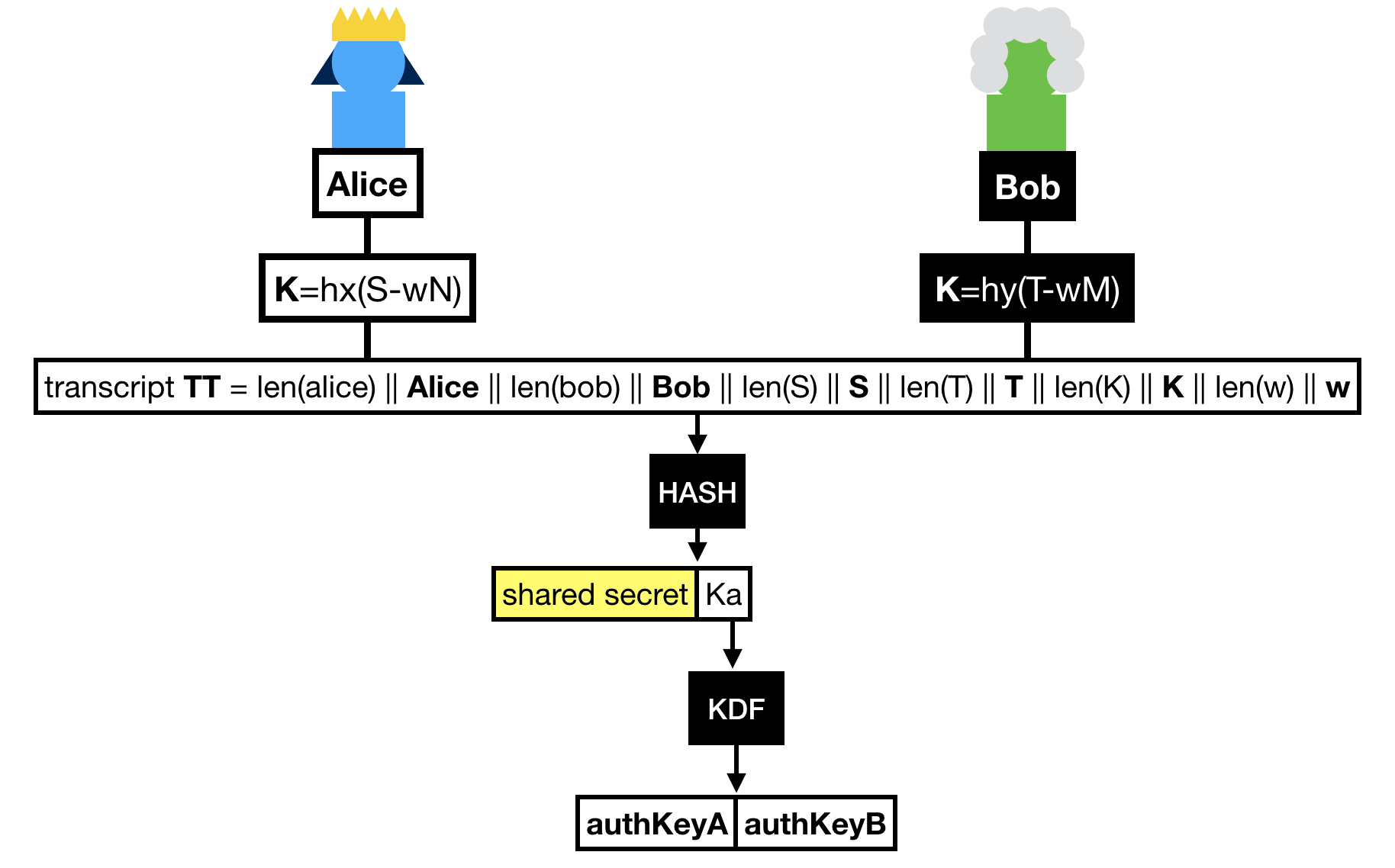
These authentication keys sole purpose is to provide key confirmation in the last round-trip of messages.
That is to say at this point, if we don't do anything, we don't know if either Alice or Bob truly managed to compute the shared secret.
Key confirmation is pretty simple, both sides just have to compute an authentication tag with one of the authentication key produced over the transcript.
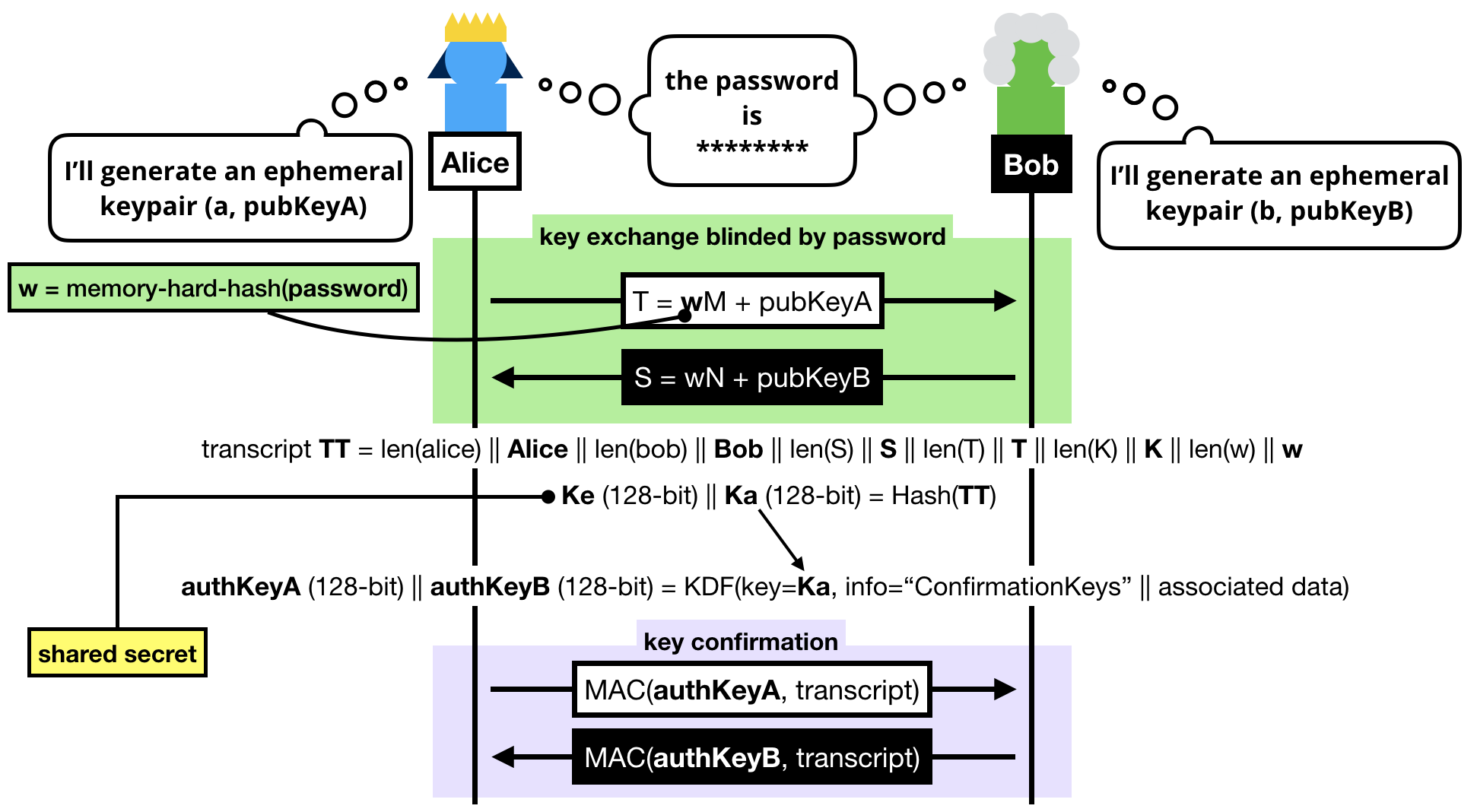
The final protocol looks a bit dense, but you should be able to decipher it if you've read this far.



















 Did you like this content? This is part of a book about how to apply modern cryptography in real world applications.
Did you like this content? This is part of a book about how to apply modern cryptography in real world applications. 


