I've participated in multiple public audits since I've started working at the Cryptography Services of NCC Group. People can often see my work through the research I do, but a good chunk of my time is spent auditing and breaking real world applications. NCC Group sometimes release public reports and I think it is a good opportunity for outsiders to see what I work on, and what the audit-part of my work looks like.
Recently, two reports were published with my name on it. The Android Pie and Nucypher PRE library.
Unfortunately we rarely release much details when we find critical vulnerabilities, so the more interesting reports are always partially published (like the Google one) or just not public. One day I'll find a way to talk about (without leaking out any information about clients of course) some of the juicy findings I and others have found in my years of consulting. Some of these war stories are extremely entertaining. We sometimes don't find much, but when we completely break a cryptocurrency or a company's flagship product, it feels like we're the best in the world at what we do.

On May 15th, I approached Yuval Yarom with a few issues I had found in some TLS implementations. This led to a collaboration between Eyal Ronen, Robert Gillham, Daniel Genkin, Adi Shamir, Yuval Yarom and I. Spearheaded by Eyal, the research has now been published here. And as you can see, the inventor of RSA himself is now recommending you to deprecate RSA in TLS.
We tested 9 different TLS implementations against cache attacks and 7 were found to be vulnerable: OpenSSL, Amazon s2n, MbedTLS, Apple CoreTLS, Mozilla NSS, WolfSSL, and GnuTLS. The cat is not dead yet, with two lives remaining thanks to BearSSL (developed by my colleague Thomas Pornin) and Google's BoringSSL.
The issues were disclosed back in August and the teams behind these projects were given time to resolve them. Everyone was very cooperative and CVEs have been dispatched (CVE-2018-12404, CVE-2018-19608, CVE-2018-16868, CVE-2018-16869, CVE-2018-16870).
The attack leverages a side-channel leak via cache access timings of these implementations in order to break the RSA key exchanges of TLS implementations. The attack is interesting from multiple points of view (besides the fact that it affects many major TLS implementations):
- It affects all versions of TLS (including TLS 1.3) and QUIC. Where the latter version of TLS does not even offer an RSA key exchange! This prowess is achieve because of the only known downgrade attack on TLS 1.3.
- It uses state-of-the-art cache attack techniques. Flush+Reload? Prime+Probe? Branch-Predition? We have it.
- The attack is very efficient. We found ways to ACTIVELY target any browsers, slow some of them down, or use the long tail distribution to repeatdly try to break a session. We even make use of lattices to speed up the problem.
- Manger and Ben-Or on RSA PKCS#1 v1.5. You heard of Bleichenbacher's million messages attack? Guess what, we found better. We use Manger's OAEP attack on RSA PKCS#1 v1.5 and even Ben-Or's algorithm which is more efficient than and was published BEFORE Bleichenbacher's work in 1998. I uploaded some of the code here.
To learn more about the research, you should read the white paper. I will talk specifically about protocol-level exploitation in this blog post.
Attacking RSA, The Origins
While Ben-Or et al. research was initially used to support the security proofs of RSA, it was none-the-less already enough to attack the protocol. But it is only in 1998 that Daniel Bleichenbacher discovers a padding oracle and devise his own practical attack on RSA. The consequences are severe, most TLS implementations could be broken, thus mitigations were designed to prevent Daniel's attack. Follows a series of "re-discovery" where the world realizes that it is not so easy to implement such mitigations:
Let's be realistic, the mitigations that developers had to implement were unrealistic. Furthermore, an implementation that would attempt to log such attacks would actually help the attacks. Isn't that funny?
The research I'm talking about today can be seen as one more of these "re-discovery". My previous boss' boss (Scott Stender) once told me: "you can either be the first paper on the subject, or the best written one, or the last one". We're definitely not the first one, I don't know if we write that well, but we sure are hopping to be the last one :)
RSA in TLS?
Briefly, SSL/TLS (except TLS 1.3) can use an RSA key exchange during a handshake to negotiate a shared secret. An RSA key exchange is pretty straight forward: the client encrypts a shared secret under the server's RSA public key, then the server receives it and decrypts it. If we can use our attack to decrypt this value, we can then passively decrypt the session (and obtain a cookie for example) or we can actively impersonate one of the peer.
Attacking Browsers, In Practice.
We employ the BEAST-attack model (in addition to being colocated with the victim server for the cache attack) which I have previously explained in a video here.
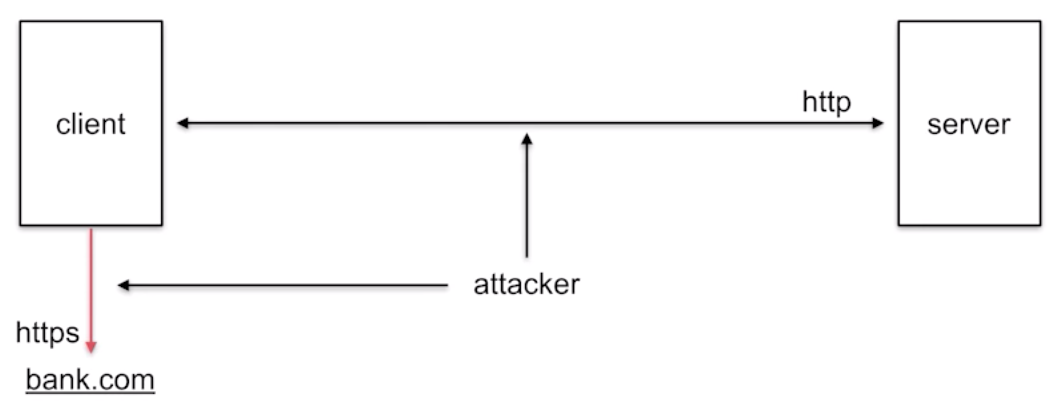
With this position, we then attempt to decrypt the session between a victim client (Bob) and bank.com: we can serve him with some javascript content that will continuously attempt new connections on bank.com. (If it doesn't attempt a new connection, we can force it by making the current one fail since we're in the middle.)
Why several connections instead of just one? Because most browsers (except Firefox which we can fool) will time out after some time (usually 30s). If an RSA key exchange is negotiated between the two peers: it's great, we have all the time in the world to passively attack the protocol. If an RSA key exchange is NOT negotiated: we need to actively attack the session to either downgrade or fake the server's RSA signature (more on that later). This takes time, because the attack requires us to send thousands of messages to the server. It will likely fail. But if we can try again, many times? It will likely succeed after a few trials. And that is why we continuously send connection attempts to bank.com.
Attacking TLS 1.3
There exist two ways to attack TLS 1.3. In each attack, the server needs
to support an older version of the protocol as well.
- The first technique relies on the fact that the current server’s public key is an RSA public
key, used to sign its ephemeral keys during the handshake, and that the
older version of TLS that the server supports re-use the same keys.
- The second one relies on the fact that both peers support an older version
of TLS with a cipher suite supporting an RSA key exchange.
While TLS 1.3 does not use the RSA encryption algorithm for its key
exchanges, it does use the signature algorithm of RSA for it; if the
server’s certificate contain an RSA public key, it will be used to sign
its ephemeral public keys during the handshake. A TLS 1.3 client can
advertise which RSA signature algorithm it wants to support (if any)
between RSA and RSA-PSS. As most TLS 1.2 servers already provide support
for RSA , most will re-use their certificates instead of updating to the
more recent RSA-PSS. RSA digital signatures specified per the standard
are really close to the RSA encryption algorithm specified by the same
document, so close that Bleichenbacher’s decryption attack on RSA
encryption also works to forge RSA signatures. Intuitivelly, we have
$pms^e$ and the decryption attack allows us to find $(pms^e)^d = pms$,
for forging signatures we can pretend that the content to be signed
$tbs$ (see RFC 8446) is $tbs = pms^e$ and obtain $tbs^d$ via the attack, which is
by definition the signature over the message $tbs$. However, this
signature forgery requires an additional step (blinding) in the
conventional Bleichenbacher attack (in practice this can lead to
hundreds of thousands of additional messages).
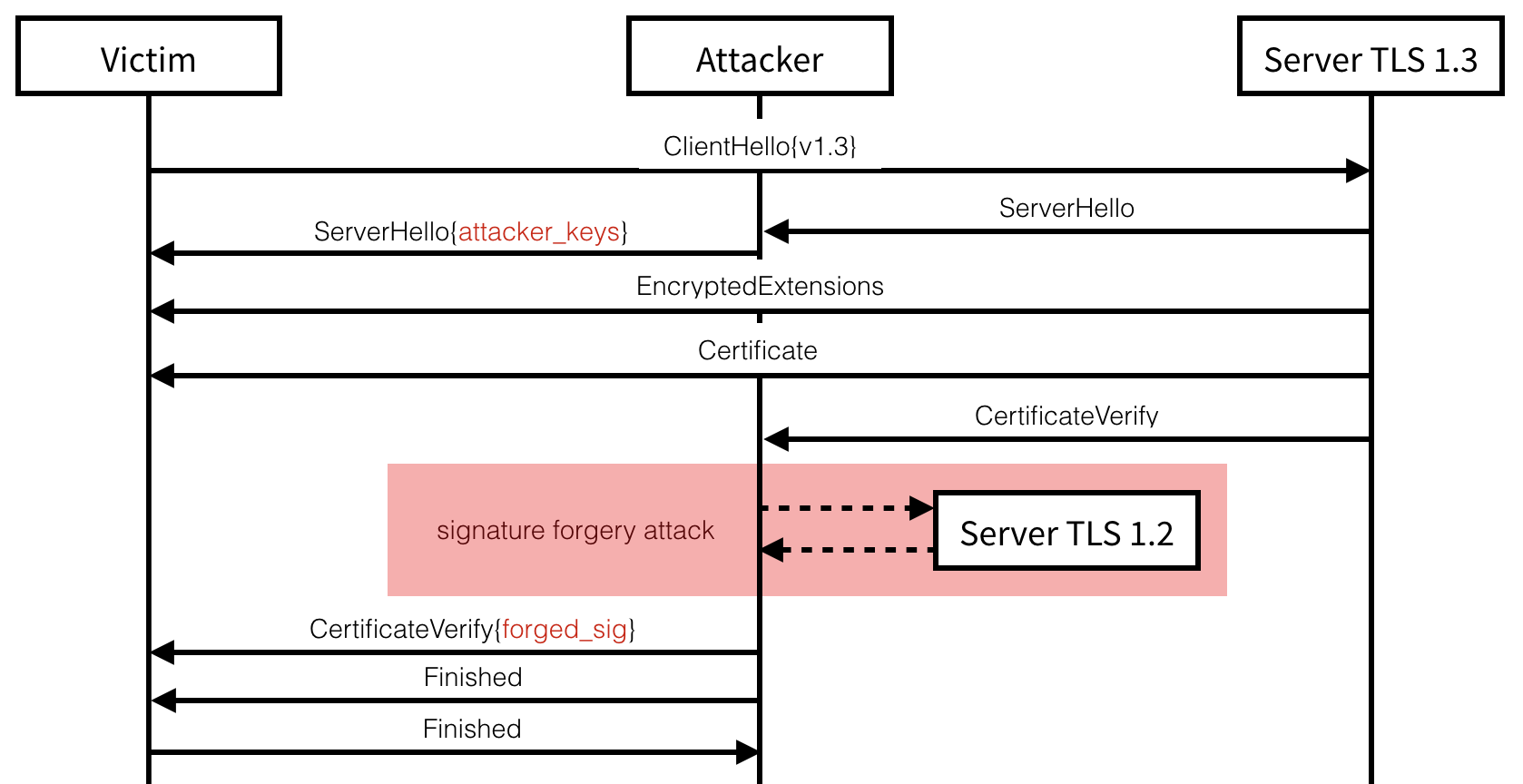
Key-Reuse has been shown in the past to allow
for complex cross-protocol attacks on TLS. Indeed, we can successfully
forge our own signature of the handshake transcript (contained in the
CertificateVerify message) by negotiating a previous version of TLS
with the same server. The attack can be carried if this new connection
exposes a length or bleichenbacher oracle with a certificate using the
same RSA key but for key exchanges.
Downgrading to TLS 1.2
Every TLS connection starts with a negotiation of the TLS version and
other connection attributes. As the new version of TLS (1.3) does not
offer an RSA key exchange, the exploitation of our attack must first
begin with a downgrade to an older version of TLS. TLS 1.3 being
relatively recent (August 2018), most servers supporting it will also
support older versions of TLS (which all provide support for RSA key
exchanges). A server not supporting TLS 1.3 would thus respond with an
older TLS version’s (TLS 1.2 in our example) server hello message. To
downgrade a client’s connection attempt, we can simply spoof this answer
from the server. Besides protocol downgrades, other techniques exist to
force browser clients to fallback onto older TLS versions: network
glitches, a spoofed TCP RST packet, a lack of response, etc. (see POODLE)
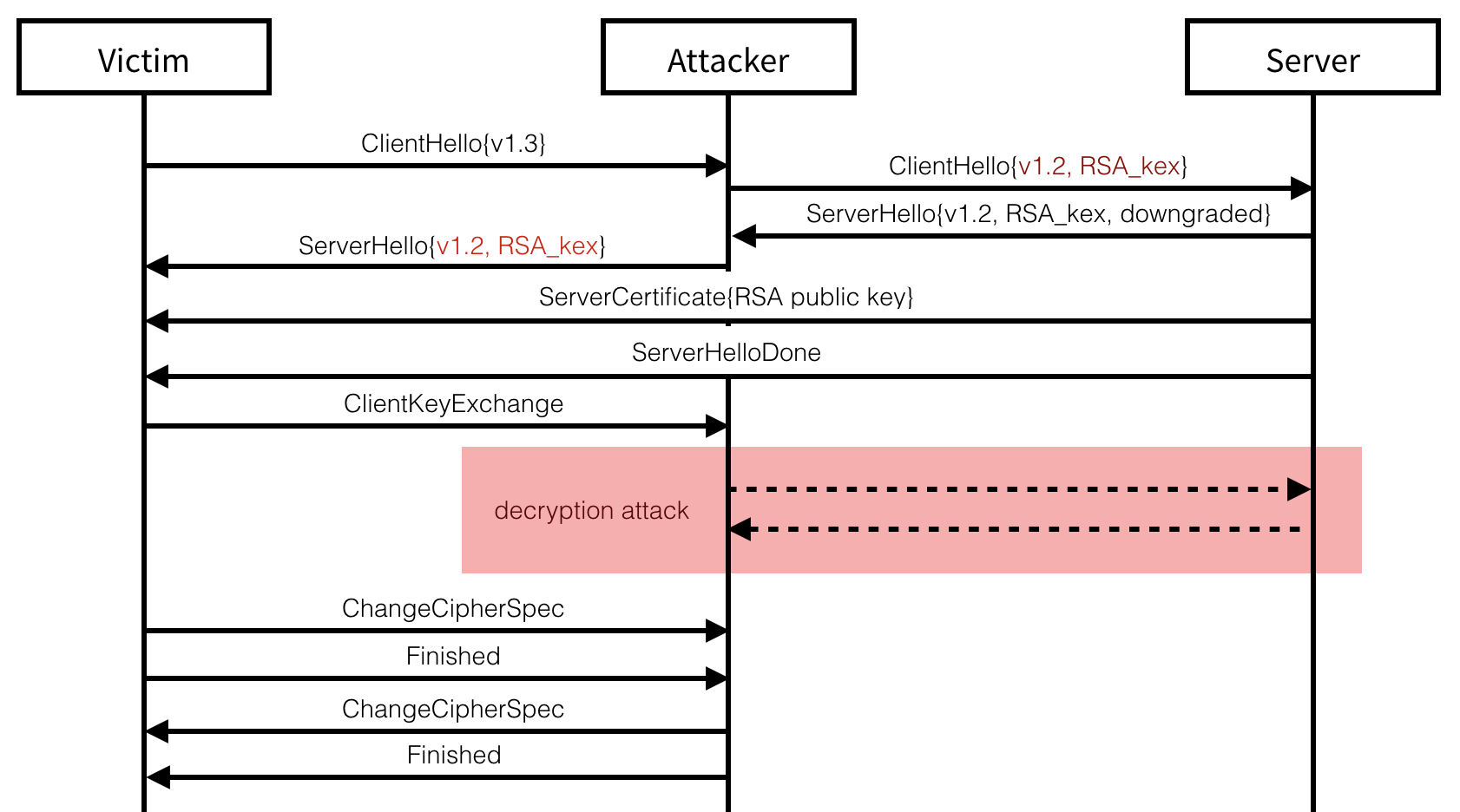
Continuing with a spoofed TLS 1.2 handshake, we can simply present the
server’s RSA certificate in a ServerCertificate message and then end
the handshake with a ServerHelloDone message. At this point, if the
server does not have a trusted certificate allowing for RSA key
exchanges, or if the client refuse to support RSA key exchanges or older
versions than TLS 1.2, the attack is stopped. Otherwise, the client uses
the RSA public key contained in the certificate to encrypt the TLS
premaster secret, sends it in a ClientKeyExchange message and ends its
part of the handshake with a ChangeCipherSpec and a Finished
messages.
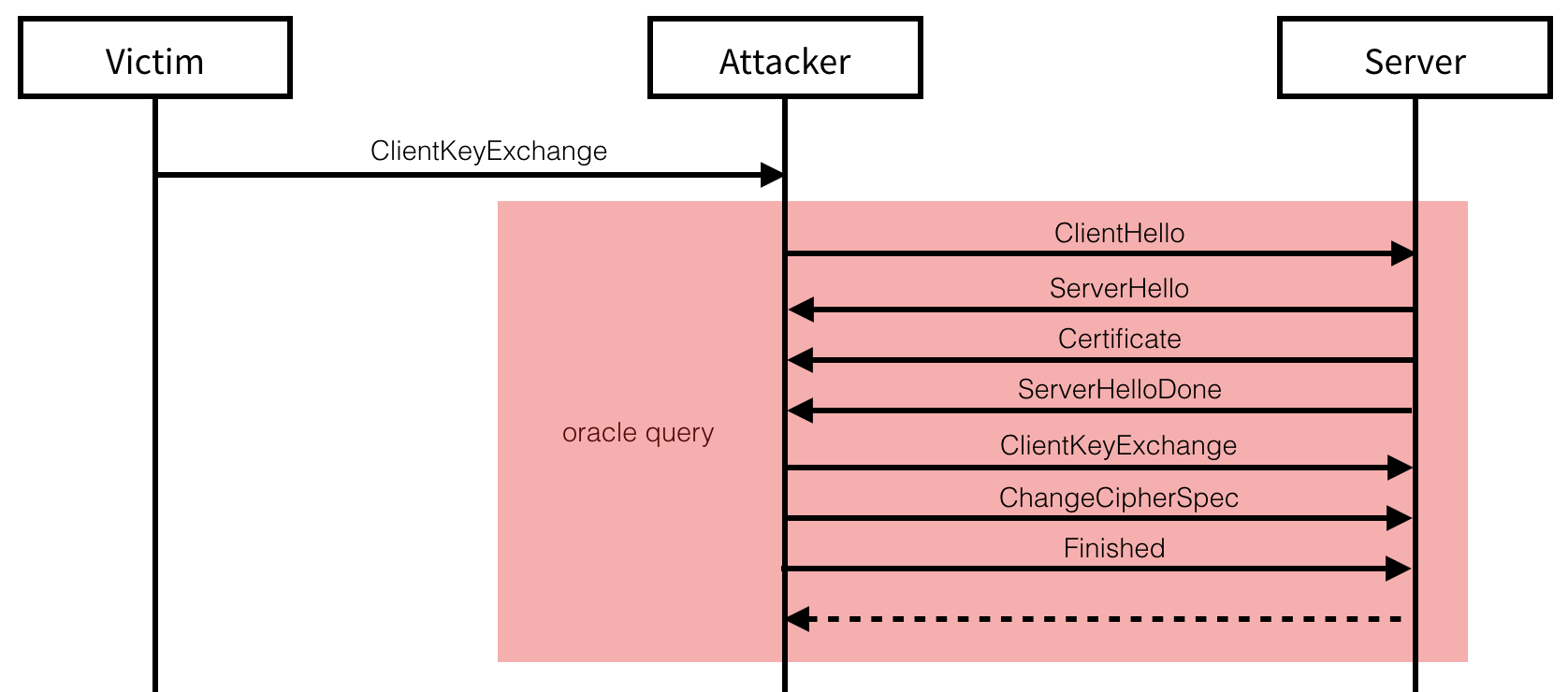
At this point, we need to perform our attack in order to decrypt the RSA
encrypted premaster secret. The last Finished message that we send must
contains an authentication tag (with HMAC) of the whole transcript, in
addition of being encrypted with the transport keys derived from the
premaster secret. While some clients will have no handshake timeouts,
most serious applications like browsers will give up on the connection
attempt if our response takes too much time to arrive. While the attack
only takes a few thousand of messages, this might still be too much in
practice. Fortunately, several techniques exist to slow down the
handshake:
Once the decryption attack terminates, we can send the expected Finished
message to the client and finalize the handshake. From there everything
is possible, from passively relaying and observing messages to the
impersonated server through to actively tampering requests made to it.
This downgrade attack bypasses multiple downgrade mitigations: one
server-side and two client-side. TLS 1.3 servers that negotiate older
versions of TLS must advertise this information to their peers. This is
done by setting a quarter of the bytes from the server_random field in
the ServerHello message to a known value. TLS 1.3 clients that end
up negotiating an older version of TLS must check for these values and
abort the handshake if found. But as noted by the RFC, “It does not
provide downgrade protection when static RSA is used.” – Since we alter
this value to remove the warning bytes, the client has no opportunity to
detect our attack. On the other hand, a TLS 1.3 client that ends up
falling back to an older version of TLS must advertise this information in their subsequent client hellos, since
we impersonate the server we can simply ignore this warning.
Furthermore, a client also includes the version used by the client hello
inside of the encrypted premaster secret. For the same reason as
previously, this mitigation has no effect on our attack. As it stands,
RSA is the only known downgrade attack on TLS 1.3, which we are the
first to successfuly exploit in this research.
Attacking TLS 1.2
As with the previous attack, both the client and the server targetted
need to support RSA key exchanges. As this is a typical key exchange
most known browsers and servers support them, although they will often
prefer to negotiate a forward secret key exchange based on ephemeral
versions of the Elliptic Curve or Finite Field Diffie-Hellman key
exchanges. This is done as part of the cipher suite negotiation during
the first two handshake messages. To avoid this outcome, the
ClientHello message can be intercepted and modified to strip it out of
any non-RSA key exchanges advertised. The server will then only choose
from a set of RSA-key-exchange-based cipher suites which will allow us
to perform the same attack as previously discussed. Our modification of
the ClientHello message can only be detected with the Finished
message authenticating the correct handshake transcript, but since we
are in control of this message we can forge the expected tag.
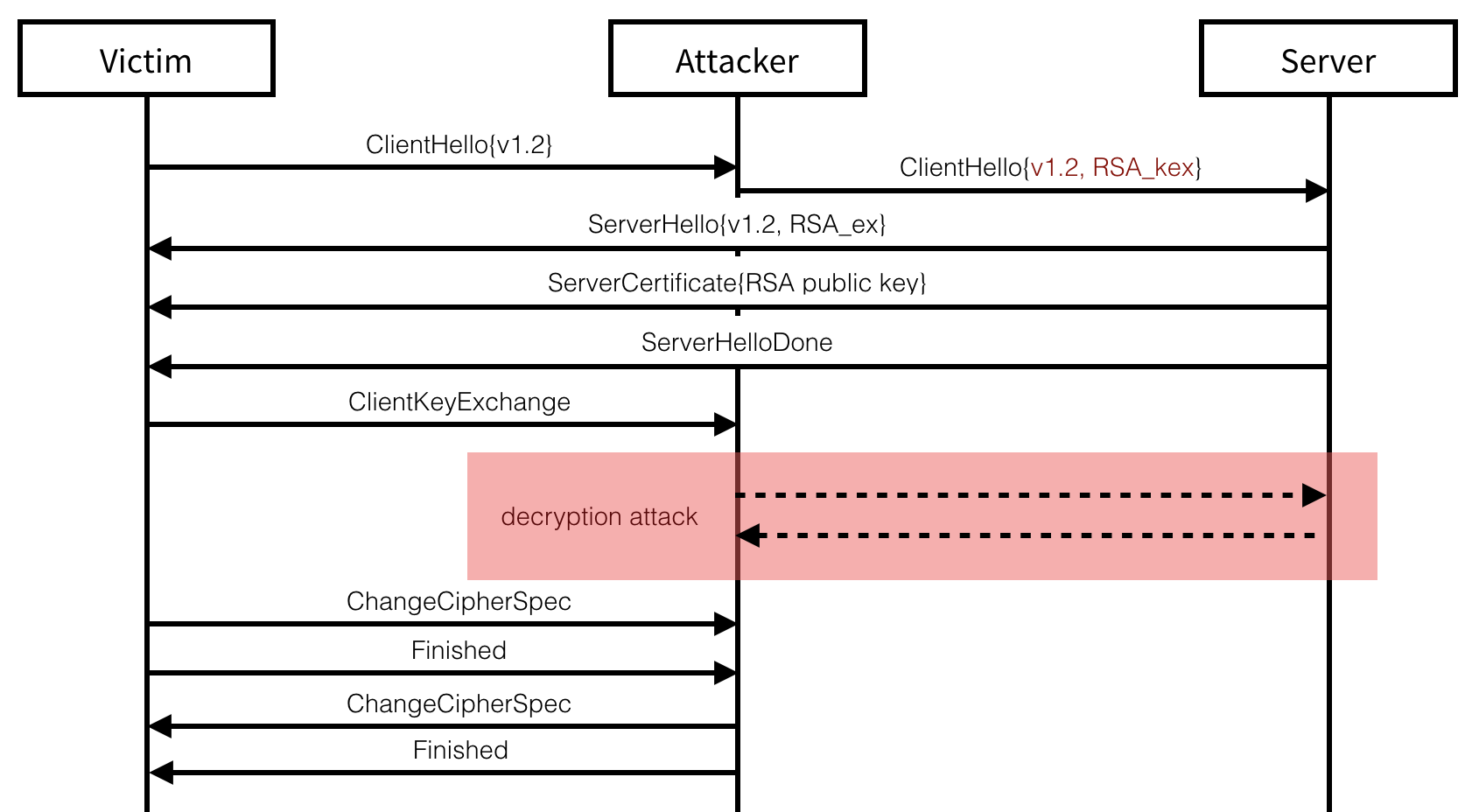
On the other side, if both peers end up negotiating an RSA key exchange
on their own, we can passively observe the connection and take our time
to break the session.
LiveOverflow recently pushed a video about Nadim Kobeissi's last paper. It is quite informative and invite to the discussion: can an end-to-end encryption app served by a webserver be secure? If you haven't seen the video, go watch it. It gives a good explanation of something that is actually quite simple. Here's someone's opinion on unnecessary complicated papers:
I have seen this kind of things happen quite often in the cryptography and security community. While some companies are 100% snake oils, some others do play on the border with their marketing claims but very real research. For example, advances in encrypted databases are mostly pushed by companies while attacks come from researchers not happy with their marketing claims. But this is a story for another time.
Back to the question: can we provide end-to-end encryption with a web app? There are ways yes. You can for example create a one-page javascript web application, and have the client download it. In that sense it could be a "trust on first use" kind of application, because later you would only rely on your local copy. If you want to make it light, have the page use remotely served javascript, images, and other files and protect manipulations via the subresource integrity mechanism of web browsers (include a hash of the file in the single-page web app). It is not a "bad" scenario, but it's not the flow that most users are used to. And this is the problem here. We are used to access websites directly, install whatever, and update apps quickly.
If you look at it from the other side, are mobile applications that more secure? While the threat model is not THAT different, in both of these solutions (thanks Nik Kinkel and Mason Hemmel for pointing that out to me) no specific targetting can happen. And this is probably a good argument if you're paranoia stops at this level (and you trust the app store, your OS, your hardware, etc.)
Indeed, a webapp can easily target you, serving a different app depending on the client's IP, whereas mobile apps need the cooperation of the App store to do that. So you're one level deeper in your defense in depth.
What about Signal's "native" desktop application? Is it any better? Well... you're probably downloading it from their webserver anyway and you're probably updating the app frequently as well...
Here's EmbeddedDisco!
I've been implementing the Disco protocol in C. It makes sense since Disco was designed specifically for embedded devices. The library is only 1,000 lines-of-code, including all the cryptographic primitives, and does everything the Go implementation does except for signing.
If you don't know what Disco is, it's a cryptographic library that allows you to secure communications (like TLS) and to hash, encrypt, authenticate, derive keys, generate random numbers, etc.
Check it out here. It's experimental. I'd be happy to receive any feedback :)
It's not as plug-and-play as the Golang version. There are no wrappers yet to encrypt, authenticate, hash, derive keys, etc. and I haven't made a decision as to what algorithm I should support for signatures (ed25519 with strobe? Or Strobe's Schnorr-variant with Curve25519?)
So it's mostly for people who know what they're doing for now.
Don't let that deter you though! I need people to play with it in order to improve the library. If you need help I'm here!
I was in Milan two weeks ago presenting on Disco at Advances in permutation-based cryptography. I prepared a few figures to show the current state of Disco.
The funny one is this realistically proportional figure where the areas of the different circles are representing the number of lines-of-code of each libraries.
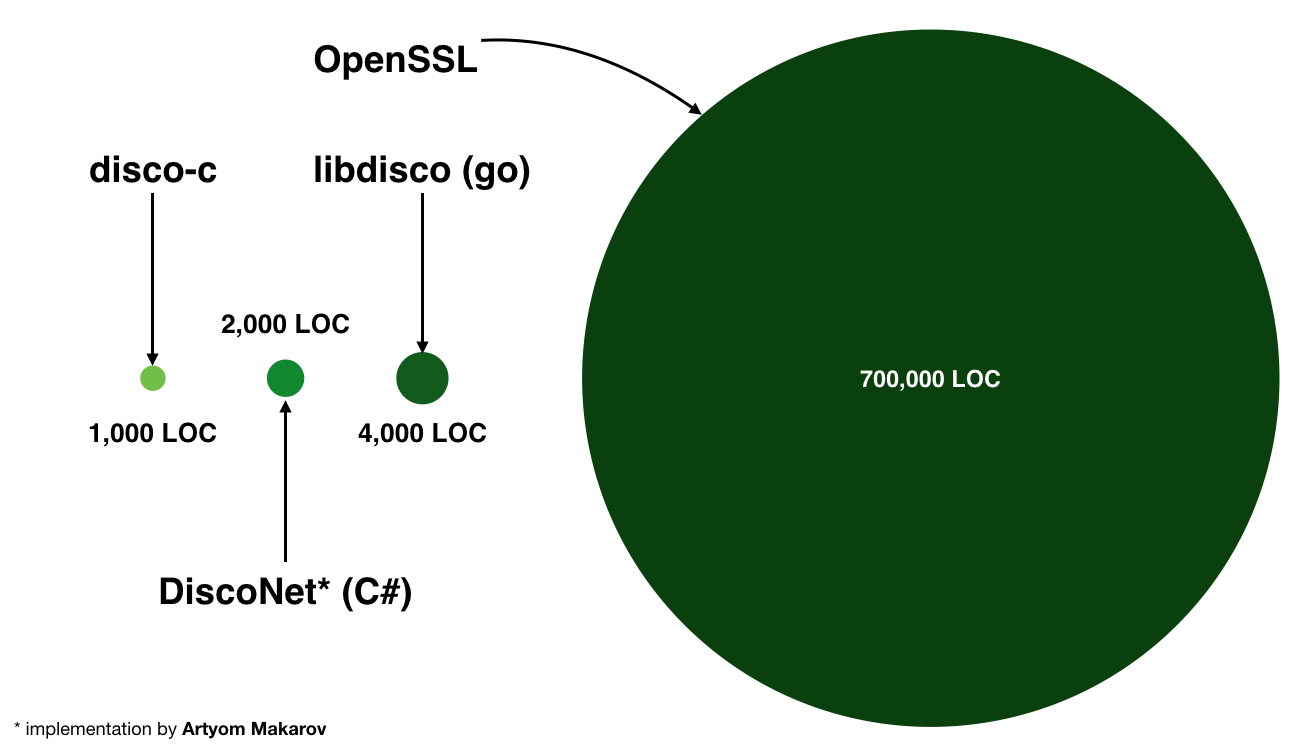
The C library is currently awful, so I won't link to it until I get it to a prettier place, but as a proof of concept it shows that this can be achieve in a mere 1,000 lines-of-code. That while supporting the same functionalities of a TLS library and even more. The following diagram is the dependency graph or "trust graph" of an implementation of Disco:

As one can see, Disco relies on Strobe (which further relies on keccak-f) for the symmetric cryptography, and X25519 for the asymmetric cryptography. The next diagram shows the trust graph of a biased TLS 1.3 implementation for comparison:

This was done mostly for fun, so I might be missing some things, but you can see that it's starting to get more involved. Finally, I made a final diagram on what most installations actually depend on:

In this one I included other versions of TLS, but not all. I also did not include their own trust graph. Thus, this diagram is actually less complex that it could be in reality, especially knowning that some companies continue to support SSL 3.0 and TLS 1.0.
I've also included non-cryptographic things like x509 certificates and their parsers, because it is a major dependency which was dubbed the most dangerous code in the world by M. Georgiev, S. Iyengar, S. Jana, R. Anubhai, D. Boneh, and V. Shmatikov.

Encrypting a file is hard. I often need to do it to protect confidential data before sending it to someone. Besides PGP (yerk) there doesn't seem to be any light tools to do that easily. The next best option is often to have a common messaging app like Signal. So I made my own. It's called Eureka and it's available in binaries or if you have Golang installed on your device, directly by doing this:
$ go get github.com/mimoo/eureka
It's also 100 LOC. It's just doing a simple job that seems to be missing from most default tooling.












