tl;dr of the sweet32 attack (On the Practical (In-)Security of 64-bit Block Ciphers) posted September 2016

I wrote about that 3-weeks-ago attack on the NCC Group's blog, but I had a bit more to say about it, so I made a tl;dr video =) enjoy!

Key Compromise Impersonation attacks (KCI) posted September 2016

You might have heard of KCI attacks on TLS: an attacker gets to install a client certificate on your device and can then impersonate websites to you. I had thought the attack was a highly impractical one, but looking at the video of the attack (done against facebook.com at the time) it seemed to contradict my first instinct.

I skimmed the paper and it answered some of my questions and doubts. So here's a tl;dr of it.

The issue is pretty easy to comprehend once you understand how a Diffie-Hellman key exchange works.

Imagine that you navigate to myCompany.com and you do a key exchange with both of your public keys.

• your public key: \(g^a \pmod{n}\)

• your company's public key: \(g^b \pmod{n}\)

where \(g\) and \(n\) are public parameters that you agreed on. Let's ignore \(n\) from now on: here, both ends can create the shared secret by doing either \((g^b)^a\) or \((g^a)^b\).

In other words, shared secret = (other dude's public key)^{(my private key)}

If you know either one of them's private key, you can observe the other public key (it's public!) and compute the shared secret. Then you have enough to replace one of the end in the TLS communication.

That's the theory.

If you replace the client's certificate with your own keypair, or know the private key of the certificate, you can break whatever key exchange they try to do with that certificate. What I mean by "break": from a key exchange you can compute the session keys and replace any party during the following communications.

My doubts had originally came from the fact that most implementations rarely use plain Diffie-Hellman, instead they usually offer ephemeral DH or RSA-based key exchanges (which are not vulnerable to this attack). The paper brought me back to reality:

Support for fixed DH client authentication has been very recently added to the OpenSSL 1.0.2 branch.

But then how would you make the client do such a un-used key exchange? The paper washed me from doubts once again:

the attacker, under the hood, interferes with the connection initialization to facebook, and forces the client to use an insecure handshake with client authentication, requesting the previously installed certificate from the system.

Now a couple of questions come to my mind.

How does facebook have these non-ephemeral DH ciphersuites?

→ from the paper, the server doesn't even need to use a static DH ciphersuite. If it has an ECDSA certificate, and didn't specify that it's only to be used to sign then you can use it for the attack (the keyUsage field in the certificate is apparently never used correctly, the few values listed in this RFC tell you how to correctly limit the authorized usages of your public key)

How can you trigger the client to use this ciphersuite?

→ just reply with a serverHello only displaying static ECDH in its ciphersuite list (contrarily to ECDHE, notice the last E for ephemeral). Then show the real ECDSA certificate (the client will interpret that as a ECDH cert because of the fake ciphersuites) and then ask the client for the specific cert you know the private key of.

In addition to the ECDSA → ECDH trumpery, this is all possible because none of these messages are signed at that moment. They are later authenticated via the shared secret, but it is too late =) I don't know if TLS 1.3 is doing a better job in this regard.

It also seems to me that in the attack, instead of installing a client cert you could just install a CA cert and MITM ALL TLS connections (except the pinned ones). But then, this attack is more sneaky, and it's another way of doing exactly this. So I appreciate that.

Fault attacks on RSA's signatures posted September 2016

Facebook was organizing a CTF last week and they needed some crypto challenge. I obliged, missed a connecting flight in Phoenix while building it, and eventually provided them with one idea I had wanted to try for quite some time. Unfortunately, as with the last challenge I wrote for a CTF, someone solved it with a tool instead of doing it by hand (like in the good ol' days). You can read the quick write up there, or you can read a more involved one here.

The challenge

The challenge was just a file named capture.pcap. Opening it with Wireshark would reveal hundreds of TLS handshakes. One clever way to find a clue here would be to filter them with ssl.alert_message.

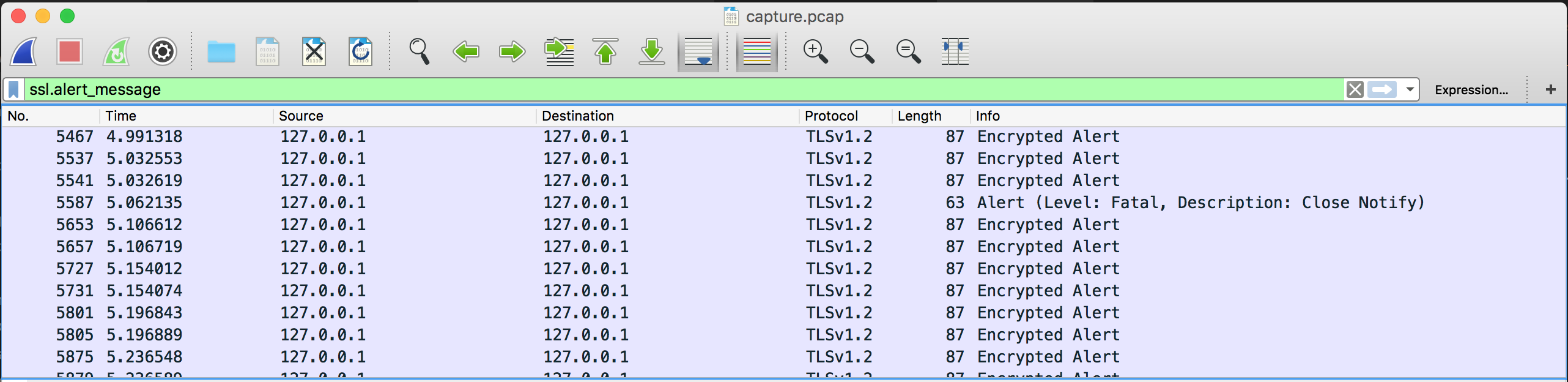
From that we could observe a fatal alert being sent from the client to the server, right after the server Hello Done.

Mmmm

Several hypothesis exist. One way of guessing what went wrong could be to run these packets to openssl s_client with a -debug option and see why the client decides to terminate the connection at this point of the handshake. Or if you had good intuition, you could have directly verified the signature :)

After realizing the signature was incorrect, and that it was done with RSA, one of the obvious attack here is the RSA-CRT attack! Faults happen in RSA, sometimes because of malicious reasons (lasers!) or just because of random errors that can happen in different parts of the hardware. One random bit shifting and you have a fault. If it happens at the wrong place, at the wrong time, you have a cryptographic failure!

RSA-CRT

RSA is slow-ish, as in not as fast as symmetric crypto: I can still do 414 signatures per second and verify 15775 signatures per second (according to openssl speed rsa2048).

Let's remember a RSA signature. It's basically the inverse of an encryption with RSA: you decrypt your message and use the decrypted part as a signature.

To verify a signature over a message, you do the same kind of computation on the signature using the public exponent, which gives you back the message:

We remember here that \(N\) is the public modulus used in both the signing and verifying operations. Let \(N=pq\) with \(p, q\) two large primes.

This is the basis of RSA. Its security relies on the hardness to factor \(N\).

I won't talk more about RSA here, so check Wikipedia) if you need a recap =)

It's also obvious for a lot of you reading this that you do not sign the message directly. You first hash it (this is good especially for large files) and pad it according to some specifications. I will talk about that in the later sections, as this distinction is not immediately important to us. We have now enough background to talk about The Chinese Remainder Theorem (CRT), which is a theorem we use to speed up the above equation.

So what if we could do the calculation mod \(p\) and \(q\) instead of this huge number \(N\) (usually 2048 bits)? Let's stop with the what ifs because this is exactly what we will do:

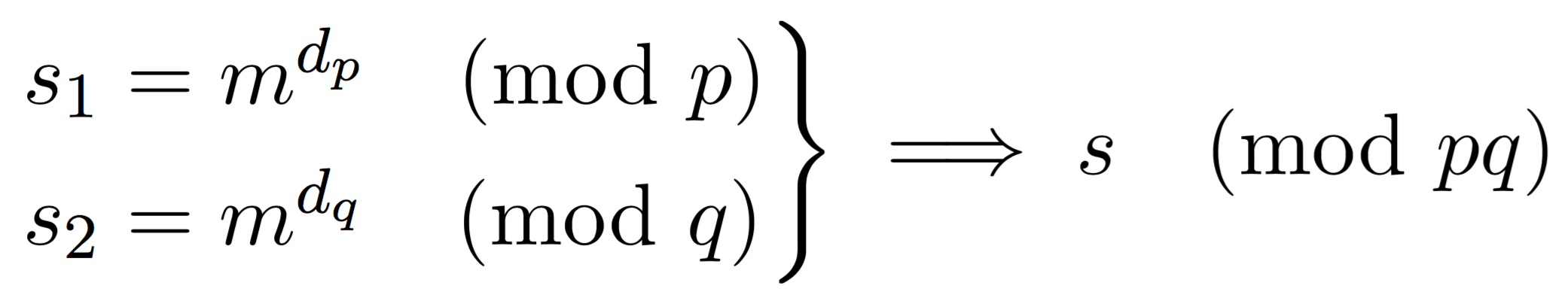
Here we compute two partial signatures, one mod \(p\), one mod \(q\). With \(d_p = d \pmod{p-1}\) and \(d_q = d \pmod{q-1}\). After that, we can use CRT to stich these partial signatures together to obtain the complete one.

I won't go further, if you want to know how CRT works you can check an explanation in my latest paper.

RSA-CRT fault attack

Now imagine that a fault happens in one of the equation mod \(p\) or \(q\):

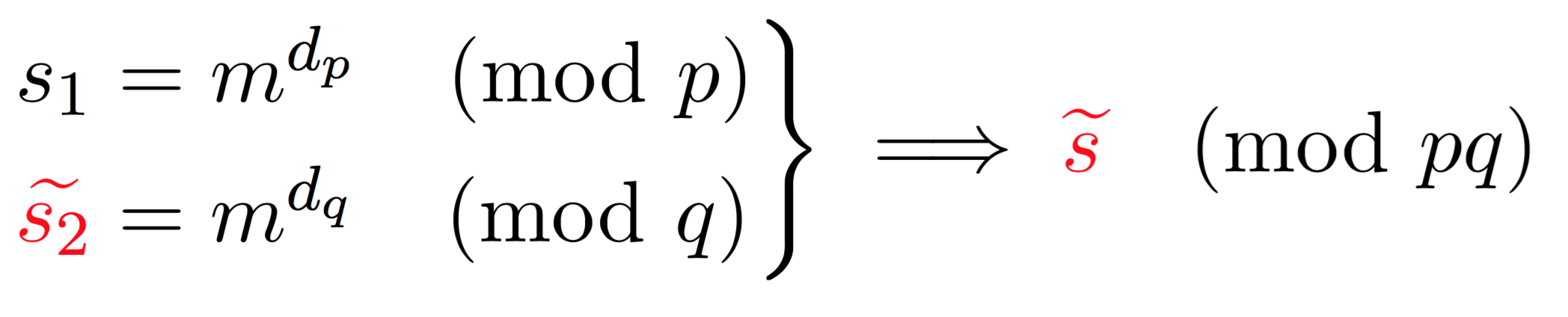
Here, because one of the operation failed (\(\widetilde{s_2}\)) we obtain a faulty signature \(\widetilde{s}\). What can we do with a faulty signature you may ask? We first observe the following facts on the faulty signature.

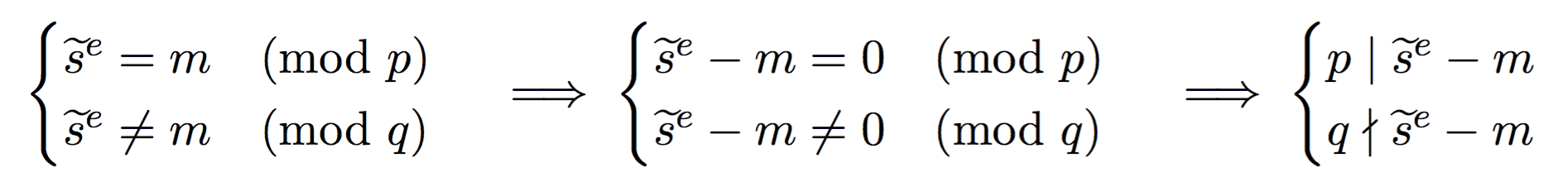
See that? \(p\) divides this value (that we can calculate since we know both the faulty signature, the public exponent \(e\), and the message). But \(q\) does not divide this value. This means that \(\widetilde{s}^e - m\) is of the form \(pk\) with some integer \(k\). What follows is naturally that \(gcd(\widetilde{s}^e - m, N)\) will give out \(p\)! And as I said earlier, if you know the factorization of the public modulus \(N\) then it is game over.

Applying the RSA-CRT attack

Now that we got that out of the way, how do we apply the attack on TLS?

TLS has different kind of key exchanges, some basic ones and some ephemeral (forward secure) ones. The basic key exchange we've used a lot in the past is pretty straight forward: the client uses the RSA public key found in the server's certificate to encrypt the shared secret with it. Then both parties derive the session keys out of that shared secret

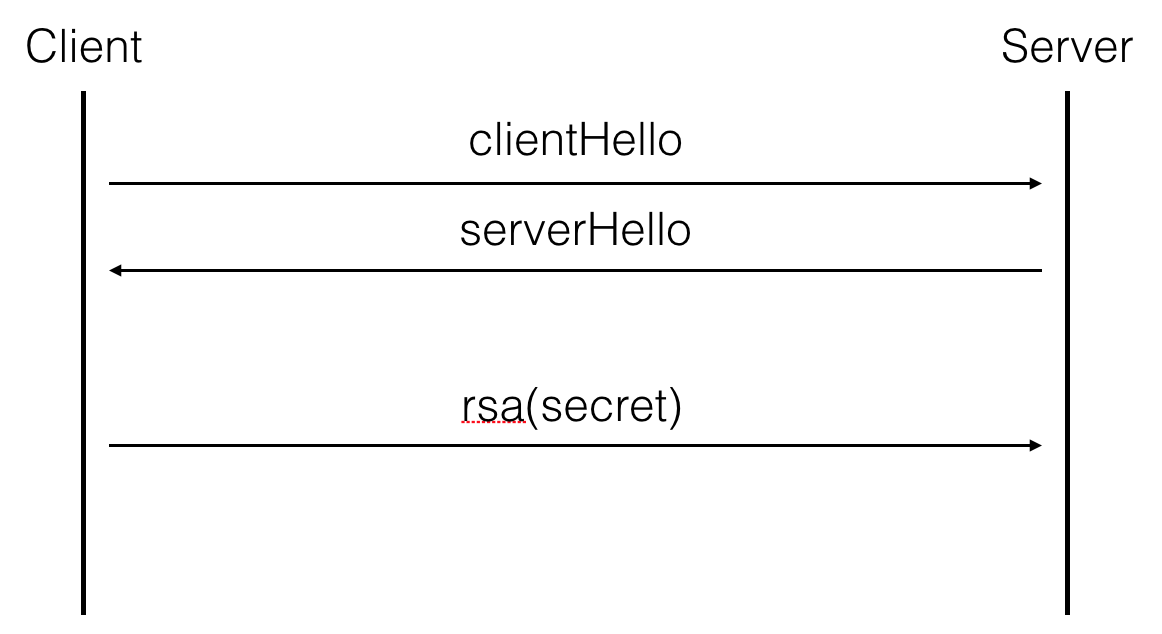
Now, if the client and the server agree to do a forward-secure key exchange, they will use something like Diffie-Hellman or Elliptic Curve Diffie-Hellman and the server will sign his ephemeral (EC)DH public key with his long term key. In our case, his public key is a RSA key, and the fault happens during that particular signature.

Now what's the message being signed? We need to check TLS 1.2's RFC:

  struct {
      select (KeyExchangeAlgorithm) {
          ...
          case dhe_rsa:
              ServerDHParams params;
              digitally-signed struct {
                  opaque client_random[32];
                  opaque server_random[32];
                  ServerDHParams params;
              } signed_params;
              ...
  } ServerKeyExchange;

• the client_random can be found in the client hello message
• the server_random in the server hello message
• the ServerDHParams are the different parameters of the server's ephemeral public key, from the same TLS 1.2 RFC:

  struct {
      opaque dh_p<1..2^16-1>;
      opaque dh_g<1..2^16-1>;
      opaque dh_Ys<1..2^16-1>;
  } ServerDHParams;     /* Ephemeral DH parameters */

  dh_p
     The prime modulus used for the Diffie-Hellman operation.

  dh_g
     The generator used for the Diffie-Hellman operation.

  dh_Ys
     The server's Diffie-Hellman public value (g^X mod p).

TLS is old, they use a non provably secure scheme to sign: PKCS#1 v1.5. Instead they should be using RSA-PSS but it's a whole different story :)

PKCS#1 v1.5's padding is pretty straight forward:

• The ff part shall be long enough to make the bitsize of that padded message as long as the bitsize of \(N\)
• The hash prefix part is a hexstring representing the hash function being used to sign

And here's the sage code!

# hash the signed_params

h = hashlib.sha384()
h.update(client_nonce.decode('hex'))
h.update(server_nonce.decode('hex'))
h.update(server_params.decode('hex'))
hashed_m = h.hexdigest()

# PKCS#1 v1.5 padding
prefix_sha384 = "3041300d060960864801650304020205000430"

modulus_len = (len(bin(modulus)) - 2 + 7) // 8
pad_len = len(hex(modulus))//2 - 3 - len(hashed_m)//2 - len(prefix_sha384)//2

padded_m = "0001" + "ff" * pad_len + "00" + prefix_sha384 + hashed_m

# Attack to recover p
p = gcd(signature^public_exponent - int(padded_m, 16), modulus)

# recover private key
q = modulus // p
phi = (p-1) * (q-1)

privkey = inverse_mod(public_exponent, phi)

What now?

Now what? You have a private key, but that's not the flag we're looking for... After a bit of inspection you realize that the last handshake made in our capture.pcap file has a different key exchange: a RSA key exchange!!!

What follows is then pretty simple, Wireshark can decrypt conversations for you, you just need a private key file. From the previous section we retrieved the private key, to make a .pem file out of it (see this article to know what a .pem is) you can use rsatool.

Tada! Hope you enjoyed the write up =)

64-bit ciphers attack in 75 hours => AES-GCM attack in 75 hours? posted August 2016

There is a new attack/paper from the INRIA (Matthew Green has a good explanation on the attack) that continues the trend introduced by rc4nomore of long attacks. The paper is branded as "Sweet32" which is a collision attack playing on the birthday paradox (hence the cake in the logo) to break 64-bit ciphers like 3DES or Blowfish in TLS.

Rc4nomore was showing off with numbers like 52 hours to decrypt a cookie. This new attack needed more queries (\(2^{32}\), hence the 32 in the name) and so it took longer in practice: 75 hours. And if the numbers are correct, this should answer the question I raised in one of my blogpost a few weeks ago:

the nonce is the part that should be different for every different message you encrypt. Some increment it like a counter, some others generate them at random. This is interesting to us because the birthday paradox tells us that we'll have more than 50% chance of seeing a nonce repeat after \(2^{32}\) messages. Isn't that pretty low?

The number of queries here are the same for these 64-bit ciphers and AES-GCM. As the AES-GCM attack pointed:

we discovered over 70,000 HTTPS servers using random nonces

Does this means that 70,000 HTTPS servers are vulnerable to a 75 hours BEAST-style attack on AES-GCM?

Fortunately not, As the sweet32 paper points out, Not every server will allow a connection to be kept alive for that long. (It also seems like no browser place a limit on the amount of time a connection can be kept alive.) An interesting project would be to figure out how many of these 70,000 HTTPS servers are allowing long-lived connections.

It's good to note that these two attacks have different results as well. The sweet32 attack targets 64-bit ciphers like 3DES and Blowfish that really nobody use. The attack is completely impractical in that sense. Whereas AES-GCM is THE cipher commonly negociated. On the other hand, while both of them are Beast-style attacks, The sweet32 attack results in decrypting a cookie whereas the AES-GCM attack only allows you to redirect the user to a valid (but tampered) https page of the misbehaving website. In this sense the sweet32 attack has directly heavier consequences.

PS: Both Sean Devlin and Hanno Bock told me that the attacks are quite different in that the 64-bit one needs a collision on the IV or on a previous ciphertext. Whereas AES-GCM needs a collision on the nonce. This means that in the 64-bit case you can request for longer messages instead of querying for more messages, you also get more information with a minimum sized query than in a AES-GCM attack. This should make the AES-GCM even less practical, especially in the case of re-keying happening around the birthday bound.

Crypto and CHES Debriefing posted August 2016

While Blackhat and Defcon are complete mayhem (especially Defcon), Crypto and CHES look like cute conferences compared to them. I've been twice at blackhat and defcon, and still can't seem to be productive and really find ways to take advantage of the learning well there. Besides meeting nice people it's more of a hassle to walk around and find what to listen to or do. On the other side, it's only my first time at Crypto and CHES but I already have an idea on how to make the most of it. The small size makes it easy to talk to great people (or at least be 2 meters away from them :D) and the small amount of tracks (2 for Crypto and 1 for CHES) makes it easy not to miss anything and avoid getting exhausted quickly from walking and waiting between talks. The campus is really nice and cozy, it's a cute university with plenty of rooms with pool tables and Foosball, couches and lounges.

The beach is right in front of the campus and most of the lunch and dinners are held outside on the campus' loans, or sometimes on the beach. The talks are sometimes quite difficult to get into, the format is of 25 minutes and the speakers are not all the time trying to pass along the knowledge but rather are trying to market their papers or checking their PHD todo list. On the bright side, the workshops are all awesome, the vendors are actually knowledgeable and will answer all your stupid questions, and posters are displayed in front of the conference with usually someone knowledgeable near by.

The rump session is a lot of fun as well, but prepare for a lot of private jokes unless you've been here for many years.

• Here are my notes on the whitebox and indistinghuishability obfuscation workshop. The tl;dr: iO is completely impractical, and probably will continue to be at least for a good decade. Cryptographically secure Whitebox currently do not exist, at least not in public publications, but even the companies involved seemed comparable to hardware vendors trying to find side-channel countermeasures: mostly playing with heuristics that raise the bar high enough (in dollars) for potential attackers to break their systems.

• Here are my notes on the smartcards and cache attacks workshop. The tl;dr is that when you build hardware that does crypto you need to go through some evaluations. Certification centers have labs for that with equipment to do EM analysis (more practical than power) and fault attacks. FIB (Focused Ion Beams) are too expensive and they will never have this kind of equipment, but more general facilities have them and you can ask to borrow the equipment for a few hours (although they never do that). Government have their own labs as well. Getting a certification is expensive and so you will probably want to do a pre-eval internally or with a third-party before that. For smartcards the consensus is to get a Common Criteria evaluation, it gives you a score calculated according to the possible attacks, and how long/how much money/how many experts they need to happen. Cache attacks in the cloud or in embedded devices where you corrupt a core/process are practical. And as with fault attacks, there is a lot you can do there.

• Here are my notes on the PROOFS workshop. No real take away here other than we've been ignoring hardware when trying to implement secure software, and we should probably continue to do so because it's a big clusterfuck down there.

I'll try to keep an up-to-date list of blogposts on the talks that were given at both Crypto and CHES. If you have any blogpost on a talk please share it in the comments and I will update this page! Also if you don't have a blog but you would be happy to write an invited blogpost on one of the talk on this blog, contact me!

• A subfield lattice attack on overstretched NTRU assumptions
• Provable Security for Symmetric Cryptography
• CRYPTO 2016 –BAKCDOORS, BIG KEYS AND REVERSE FIREWALLS ON COMPROMISED SYSTEMS
• Crypto 2016: Breaking the Circuit Size Barrier for Secure Computation Under DDH
• Paul Kocher's keynote
• CHES 2016: Flush, Gauss, and Reload – A Cache Attack on the BLISS Lattice-Based Signature Scheme
• CHES 2016: On the Multiplicative Complexity of Boolean Functions and Bitsliced Higher-Order Masking
• Elliptic Curves at Crypto and Ches
• Crypto 2016 videos
• CHES 2016 videos

Besides that, we had a panel at CHES that I did not pay too close attention too but Alex Gantman from Qualcomm said a few interesting things: 10 years ago, in 2006, was already a year before the first iPhone, and two years before the first android phone. Only 20 years ago did we discover side-channel attacks and stack smashing for fun and profit was released. Because of that it is highly questionable how predictable the next 10 years will be. (Although I'm sure car hacking will be one of the new nest of vulns). He also said something along the lines:

I've never seen, in 15 years of experience, someone saying "you need to add this security thingy so that we can reach regulation". It is usually the other way around: "you don't need to add more security measures, we've already reached regulation". Regulations are seen as a ceiling.

And because I asked a bunch of questions to laser people (thanks to AlphaNov, eShard and Riscure!), here's my idea on how you would go to do a fault attack:

• You need to get a laser machine. Riscure and a bunch of others are buying lasers from AlphaNov, a company from Bordeaux!
• You need to power the chip you're dealing with while you do your analysis
• look at the logic, it's usually the smallest component on the chip. The biggest is the memory.
• You need a trigger for your laser, which is usually made with an FPGA because it needs to be fast to create the laser beam. It usually takes 15 nanoseconds with more or less 8 picoseconds.
• You can see, with infrared camera, through the silicium where your laser is hitting as well. This way if you know where to hit, you can precisely set the hitting point.
• The laser will go through the objective of the microscope you're using to observe the chip/IC/SoCs with.
• Usually since you're targeting the logic and it's small you can't see the gates/circuit, so you blindly probe it with short burst of photons, cartographying it until you find the right XOR or operation you are trying to target.
• It seems like you would also need to use test vectors for that: known plaintext/ciphertext pairs where you know what the fault is supposed to look like on the ciphertext (if you're targeting an encryption)
• Once you have the right position, you're good to try your attack.

Anyway! Enough for the blogpost. Crypto will be held at Santa Barbara next year (comme toujours), and CHES will be in Taiwan!

Security Proofs for Embedded Systems (PROOFS) posted August 2016

Crypto and CHES are now over. As always, a tiny conference takes place the day after CHES: the Security Proofs for Embedded Systems or PROOFS.

Yuval Yarom - Thwarting cache-based side-channel attacks

Microarchitectures implement a specification called the instruction set architecture (ISA), and lots of the time it's about a lot more than the ISA!

There is contention at one place, the cache! Since it's shared (because it's smaller than the memory), if we know where the victim's memory is mapped in the cache, you have an attack!

(slides from hardware secrets)

Yarom explained the Prime+Probe attack as well, where you load a cache-sized buffer from the memory and see what the victim is replacing there. This attack is possible on the L1 cache as well as the LLC cache. For more information on these attacks check my notes on the CHES tutorial. He also talked about the Flush+Reload. The whole point was to explain that constant-time is one way to circumvent the problem.

You can look at these attacks in code with Yarom's tool Mastik. The Prime+Probe is implemented on the L1 cache just by filling the whole cache with a calloc (check L1-capture.c). It's on the whole cache because it's the L1 cache that we're sharing with the victim process on a single core, the LLC attack is quite different (check L3-capture.c).

Note that I don't agree here because constant-time doesn't mean same operations done/calls accessed. For example see "padding time" techniques by boneh, braun and jana.

But the 3-rules definition of Yarom for constant-time programming is quite different from mine:

• no instructions with data-dependent execution time
• no secret-dependent flow control
• no secret-dependent memory access

To test for constant-time dynamically, we can use ctgrind, a modified valgrind by Adam Langley. We can also do some static source analysis with FlowTracker, but doesn't always work since the compiler might completely change expected results. The last way of doing it is binary analysis with CacheAudit, not perfect either.

Interestingly, there were also some questions from Michael Hamburg about fooling the branch predictor and the branch predictor target.

Stjepan Picek - Template Attack vs. Bayes Classifier

Profiled Attacks are one of the most powerful side-channel attacks we can do. One of them is Template Attack, the most powerful attack from the information theoretic point of view. Machine Learning (ML) is used heavily for these attacks.

What's a template attack? Found a good definition in Practical Template Attacks

The method used in the template attack is as follows: First a strategy to build a model of all possible operations is carried out. The term “all possible operations” usually refers to the cryptographic algorithm (or a part of it) being executed using all possible key values. The model of captured side-channel information for one operation is called template and consists of information about the typical signal to expect as well as a noise-characterization for that particular case. After that, the attack is started and the trace of a single operation (e.g. the key-scheduling of an algorithm) is captured. Using the templates created before which represent all key-values, the side-channel information of the attacked device is classified and assigned to one or more of the templates. The goal is to significantly reduce the number of possible keys or even come up with the used key

Someone else explained to me with an example. You encrypt many known plaintext with AES, with many different keys (you only change the first byte, so 256 possible ones), then you obtain traces and statistics on that. Then you do the real attack, obtain the traces, compare to find the first byte of the key.

The simplest ML attack you can do is Naive Bayes where there is no dependency (so the opposite of a template attacks). Between Naive Bayes and Template attacks, right in the middle, you have Averaged One-Dependence Estimators (A0DE)

Stjepan also talked about Probably approximately correct learning (PAC learning) but said that although it's great you couldn't use it all the time.

Sylvain Guilley - Optimal Side-Channel Attacks for Multivariate Leakages and Multiple Models

In real life, leakages are multi-variate (we have traces with many points) as well as multi-model (we can use the hamming weight and other ways of finding bias).

You acquire traces (usually called an acquisition campaign), and then make a guess on the bytes of the key: it will give you the output of the first Sbox. If we look at traces, we want to get all the information out of it so we uses matrices to do the template attack.

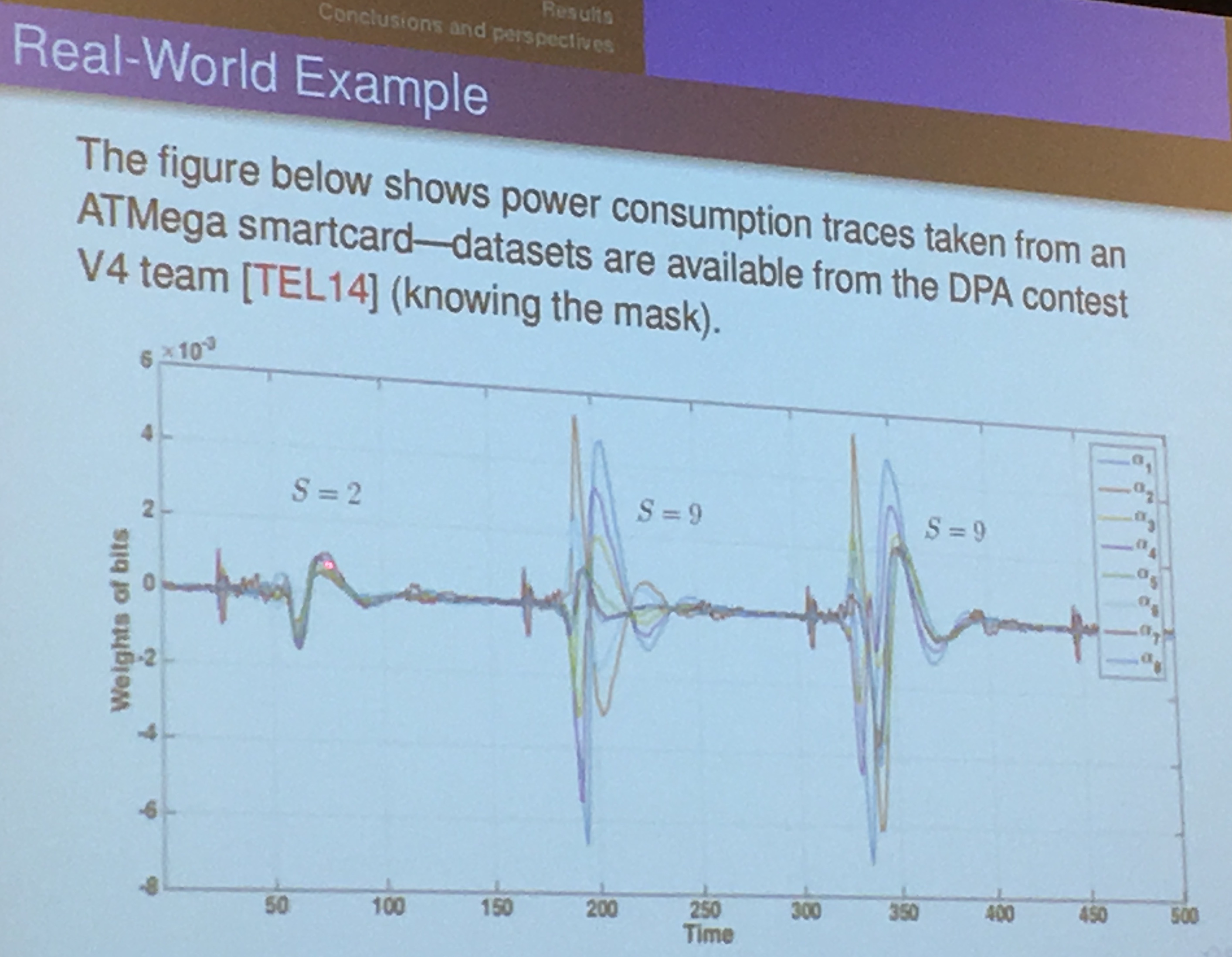
you find the \(\alpha\) by doing many measurements (profiling), the matrix will be well-conditioned and not ill-conditioned (unless you have redundant data, which never happens in practice).

In the field of numerical analysis, the condition number of a function with respect to an argument measures how much the output value of the function can change for a small change in the input argument. This is used to measure how sensitive a function is to changes or errors in the input, and how much error in the output results from an error in the input.

Jakub Breier - Mistakes Are Proof That You Are Trying: On Verifying Software Encoding Schemes' Resistance to Fault Injection Attacks

The first software information hiding scheme was done in 2001: dual-rail precharge logic (DPL) to reduce the dependence of the power consumption on the data. It's also done on software and that's what they looked at.

Static-DPL XOR uses look-up tables to implement all the logical gates. Bit Slicing is used as well, and 1 is encoded as 01, and 0 encoded as 10.

Bit slicing is a technique for constructing a processor from modules of smaller bit width. Each of these components processes one bit field or "slice" of an operand. The grouped processing components would then have the capability to process the chosen full word-length of a particular software design.

for example, bitslicing AES would mean convert all operations to operations like AND, OR, XOR, NOT that take two bits at most as input, and parallelize them all.

The static-DPL XOR's advantage is that any intermediate value at any point of time has a Hamming weight of 4. It is apparently explained further in the Prince cipher paper

Device-specific encoding XOR is minimizing the variance of the encoded intermediate values.

They wrote a fault simulator in java, doing bit flips, random byte fault, instruction skip and stuck-at fault. It seems that according to their tests only the Static-Encoding XOR would propagate faults.

Margaux Dugardin - Using Modular Extension to Provably Protect Edwards Curves Against Fault Attacks

Fault attacks can be

• safe-error attacks if it's done on a dummy operation
• cryptosystems parameters alteration
• aiming for Differential Fault Analysis DFA (bellcore attack, sign-change attacks)

If you look at double and add for elliptic curves

countermeasure is to verify the input/ouput to see if it's on the right curve. But it's ineffective against sign-change faults (Blomer et al.)

A countermeasure for that is to use Shamir's countermeasure. You do another computation in a different field (In an integer ring actually, \(Z_{pr}\) in the picture).

BOS countermeasure: You can also do the other computation on another smaller curve (Blomer et all)

But this countermeasure is not working for Weierstrass curves. To correct BOS' countermeasure they defined the curve to be an edwards curve or a twisted edwards curve.

Ryan Kastner - Moving Hardware from “Security through Obscurity” to “Secure by Design”

For Ryan, the bigger iceberg (see Yarom's talk) is the hardware we don't think about when we want to design secure software.

System of Chips design are extremely complex, we take years to develop them and we release them "forever". After that no patch. We need to get it right the first time.

Everything is becoming more and more complex. We used to be able to verify stuff "easily" with Verilog

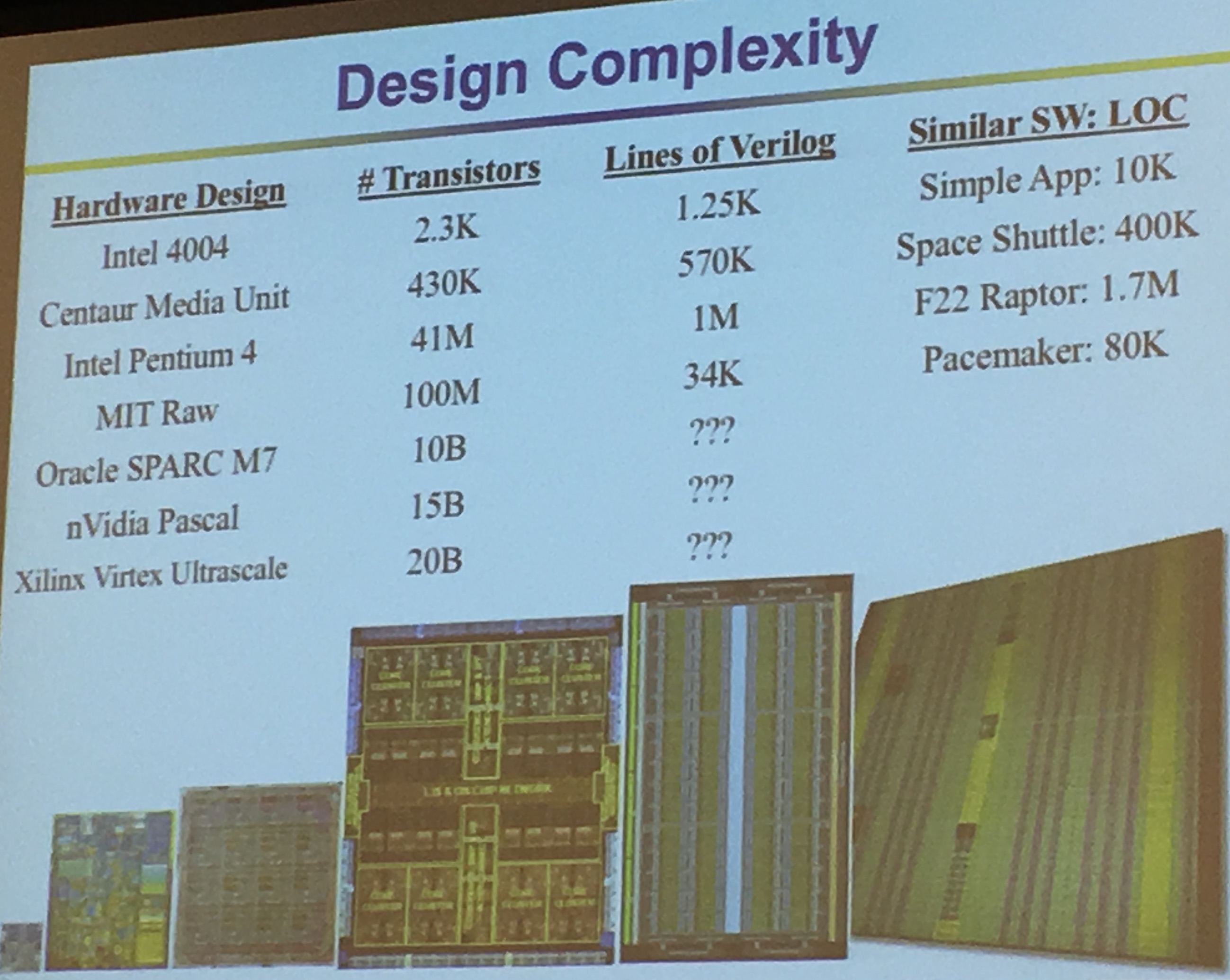
Mike Keating estimates that there is one bug for 10 lines of code in SoCs (from the art of good design). RedHat Linux has an evaluation thingy called Best Effort Safety (EAL 4+), it costs $30-$40 per LOC. Integrity RTOS: Design for Formal Evaluation (EAL 6+) is $10,000 for LOC. For big systems we can't really use them...

A lot of constructors do security through obfuscation (look at ARM, Intel, ...). It's to hard to get back the RTL, by appeal to authority (e.g. "we're Intel"), by hand waving (e.g. "we do design reviews")...

They look directly at gates, and one of the input bit is untrusted, the output is untrusted. Unless! If we have a trusted 0 input AND'ed with an untrusted input. The untrusted input won't influence the output so the output will be trusted (i.e. 0 & 1 = 0 and 0 & 0 = 0).

Looks likes they're using GLIFT to do that. But they're also looking to commercialize these ideas with Tortuga Logic.

Because they look at things from such a low perspective they can see timing leaks and key leaks and etc...

It took them about 3 years to transform the theoretical research into a commercialized product.

Matthias Hiller - Algebraic Security Analysis of Key Generation with Physical Unclonable Functions

Physical Unclonable Functions (PUFs) allows you to derive a unique fingerprint, if you want to get a key out of that you need to derive it into the right format.

Static RAM (SRAM) is a way to build PUFs, if uninitialized the bits are set "randomly" which you can use to generate your first randomness.

Apparently some PUFs have 15% of errors. Others might have 1%. A lot of work needs to be done in error correction. But error correcting codes (ECC) can leak data about the key! Their work is to work on an upper bound on what is leaked by the ECC.

PUF works by giving you a response, more from wikipedia:

Rather than embodying a single cryptographic key, PUFs implement challenge–response authentication to evaluate this microstructure. When a physical stimulus is applied to the structure, it reacts in an unpredictable (but repeatable) way due to the complex interaction of the stimulus with the physical microstructure of the device. This exact microstructure depends on physical factors introduced during manufacture which are unpredictable (like a fair coin). The applied stimulus is called the challenge, and the reaction of the PUF is called the response. A specific challenge and its corresponding response together form a challenge–response pair or CRP. The device's identity is established by the properties of the microstructure itself. As this structure is not directly revealed by the challenge-response mechanism, such a device is resistant to spoofing attacks.

They algebraically transformed the properties of a PUF, using a matrix, to facilitate their proofs:

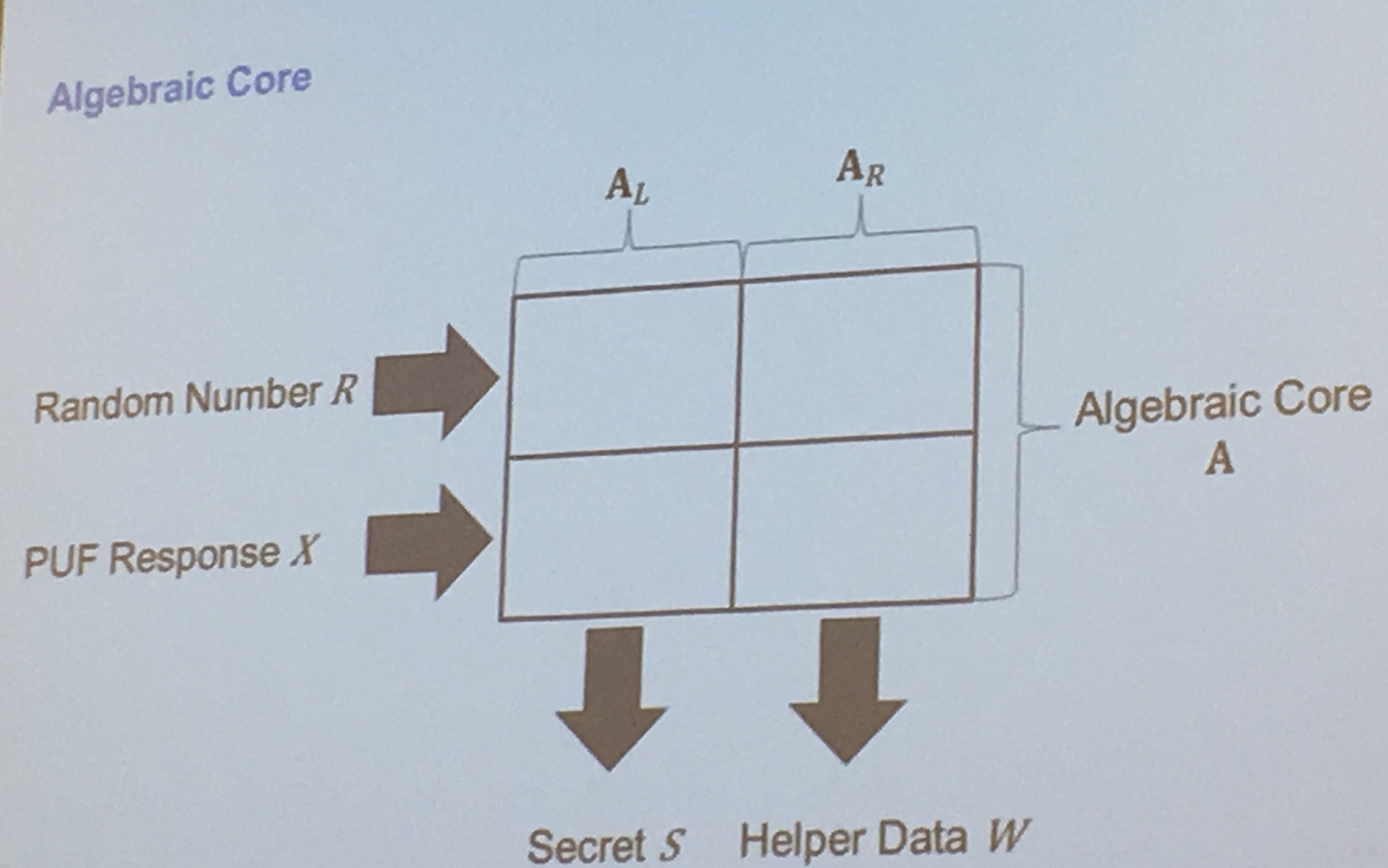
sometimes a PUF response is directly used as a key, here's how they get the algebraic representation of key generation for PUFs:

CHES 2016 tutorial part 2: Micro-Architectural Side-Channel Attacks posted August 2016

You can read part 1 here.

Yuval Yarom starts the afternoon of the workshop with a few slides on timing attacks, showing us that they are becoming more and more common in hardware. Eventhough OpenSSL classifies timing attacks as low severities, because they are hard to perform, Yarom thinks they are easy to perform.

He has a tool called "Mastik" for Micro-Architectural Side-channel toolkit. It currently implements prime+probe on L1-D, L1-l, L3 and flush+reload. There is no documentation, and he's hopping we'll give him feedback in the future. The slides and the Mastik tools are here.

Yarom starts by classifying these kind of attacks: by core shared, packet shared, system shared...

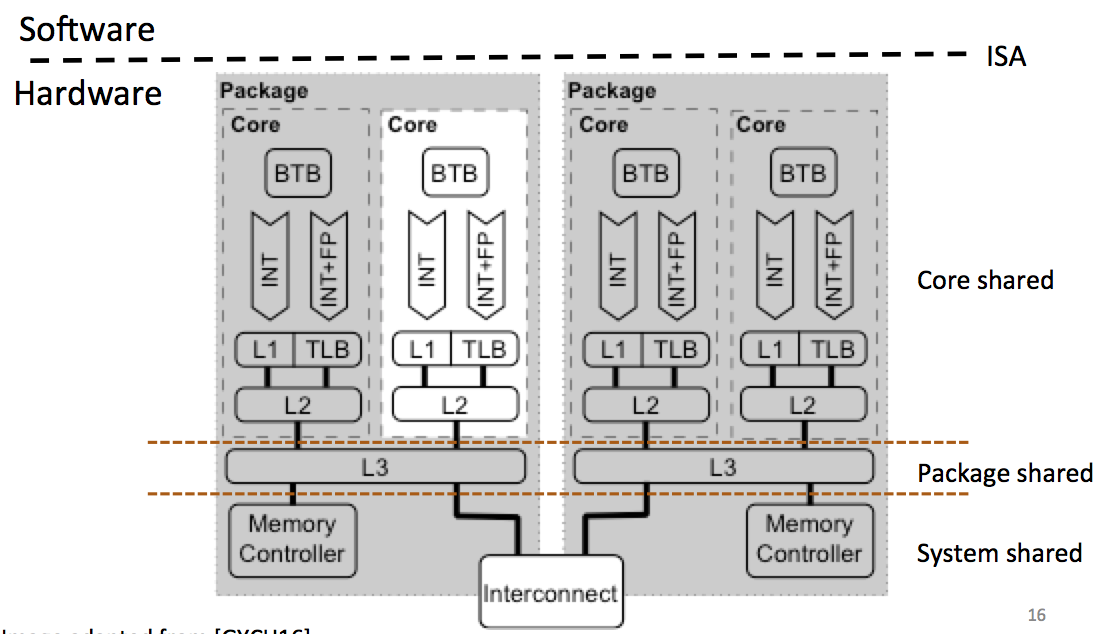
With time, the number of processors are increasing, so our odds of running on the same core as the victim are decreasing.

He then looks at other ways to classify attacks: persistent-state attacks and transient-state attacks. The second one needs the attacker and the victim running at the same time it seems.

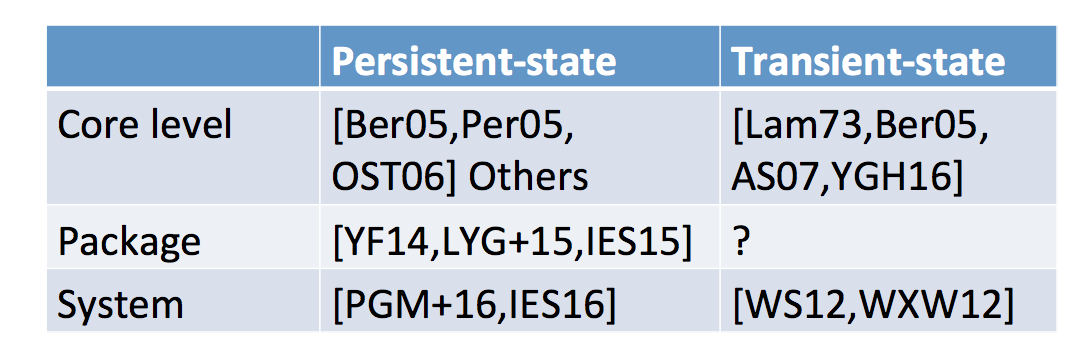
Other classifications he talks about are:

• time-driven, trace-driven, access-driven. This classification makes more sense if you look at how you do the attack, which is not great according to Yarom.
• Internal vs external contention: if the contention is internal then you can do a remote attack (the AES timing attack of djb on OpenSSL)
• degree of concurrency (multicore, hyperthreading, time slicing)

Yarom then switch the topic to memory. Memory is slower than the processor and that's why they build the cache. It's a more expensive technology and much closer to the CPU so it is faster than memory access. The CPU uses the cache to store the recent lines of memory read there. If you have many cores, the other cores can use what has been cached by one of them, and so you save time.

Inconsistency between memory and cache happens. So sometimes you want to flush the data in the cache to make sure that the next load is served directly from the memory (where it is insured to be correct). That's the basis of the flush+reload attack!

A bit of recap on memory: processes execute themselves within a virtual address space (addresses are "fake"). Then these fake addresses are mapped to physical memory addresses. This way processes don't collude in memory. and don't need to use crazy addresses (they can start at zero).

We use "sharing" of cache to save physical memory. Think shared libraries. If two programs use the same shared library, we can map this shared library to the same location. The operating system can be more agressive and do page deduplication: it detects duplicated memory patterns and de-duplicate them, removing one of them, then mapping the two program to the same region in memory. If one of the processes then wants to modify some of that shared memory, the system will copy it somewhere else so that he can do that. It was very popular with hypervisors back then but since cache attacks are a thing we don't do that anymore.

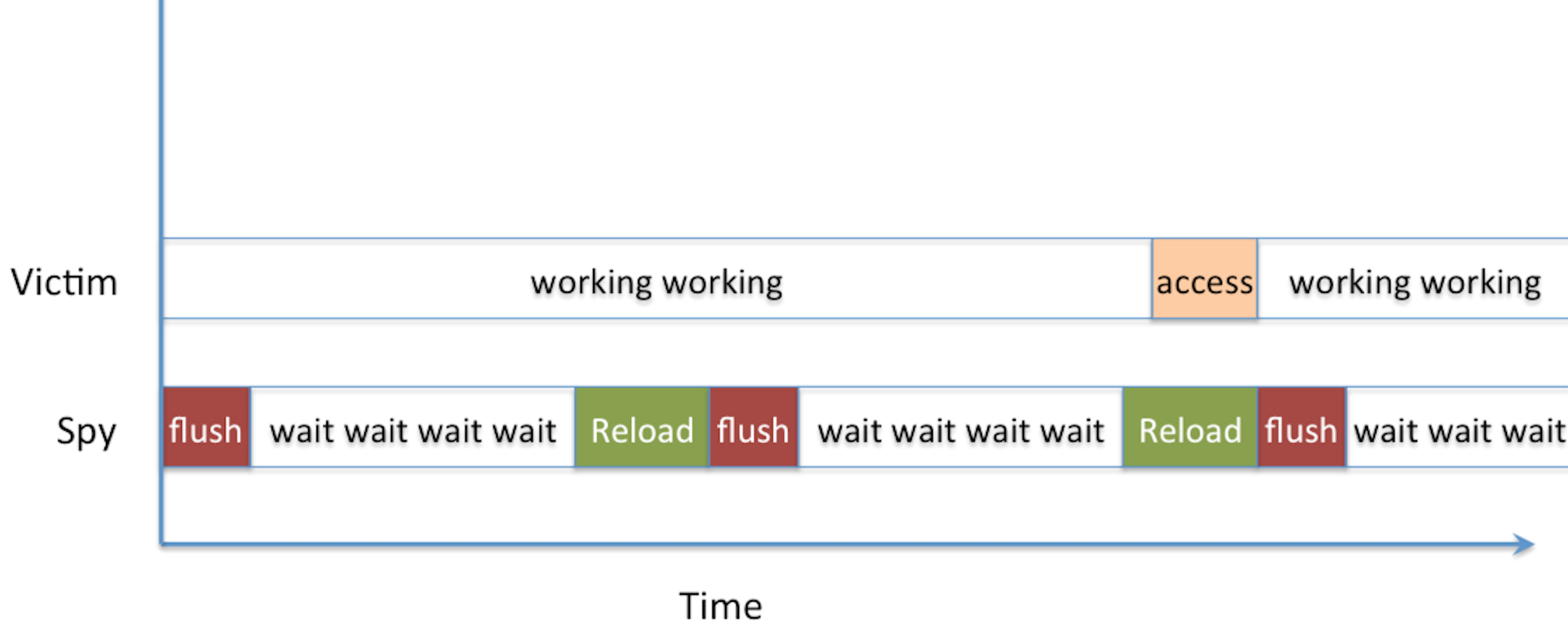
The Flush+Reload attack is straight-forward: you wait a bit, then you read from memory (it will cache it) and then you flush that cache position. Then you do that again and again and again. If a read takes a long time, it's normal. If it doesn't, it means someone else accessed it in memory and it was cached. The assembly of the attack looks like that:

mfence
rdtscp
mov %eax, %esi
mov (%ebx), %eax
rdtscp
sub %esi, %eax
clflush 0(%ebx)

clflush is the instruction to flush the cache, rdtscp takes the time (rather the number of cycles since boot). So you can compute the delta of the two rdtscp to get a runtime of the mov operation in between.

He demoed the thing via his tool FR-1-file-access.c. The program is pretty short and concise, it monitored a file continuously via reading and flushing, until it detected the use of the unix tool cat on the monitored file triggered by Yarom in another terminal. The code figures that a slow-read happened if it takes more than 100 cycles, it's not always a 100 so you have this FR-threshold.c program that you can use to see how long is the wait from a short-read to a long-read. If you want to play with the file, do a make in src/, then a make in demo.

After that he showed how to monitor calls to a function, in particular the standard C functionputs. He used nm /usr/lib64/libc-2.17.so | grep puts to get the offset of the function puts in memory, then FR-function-call let us monitor that position in memory.

One problem arrises if the victim access our monitored position right after we've reloaded the data from memory into the cache and right before we had time to flush it. The victim would then benefit from our load and get a short-read, and we will miss his access. That's a probe miss.

He then demoed an attack on GnuPG via the tool FR-gnupg-1.4.13.c, in particular the square and multiply algorithm inside GnuPG. The goal here is as usual to detect square-reduce from square-reduce-multiply-reduce operations, this would allow you to deduce the private exponent.

He looked at the code of GnuPG and noticed that they were using the lines 85, 281, etc... in the code. And then used gdb to see what were the addresses in memory for these lines (you can do the same using debuginfo.sh)

Yarom ran GnuPG to sign a file, while he ran FR-gnupg-1.4.13.c. He then gnuploted the results of his monitoring to look for patterns.

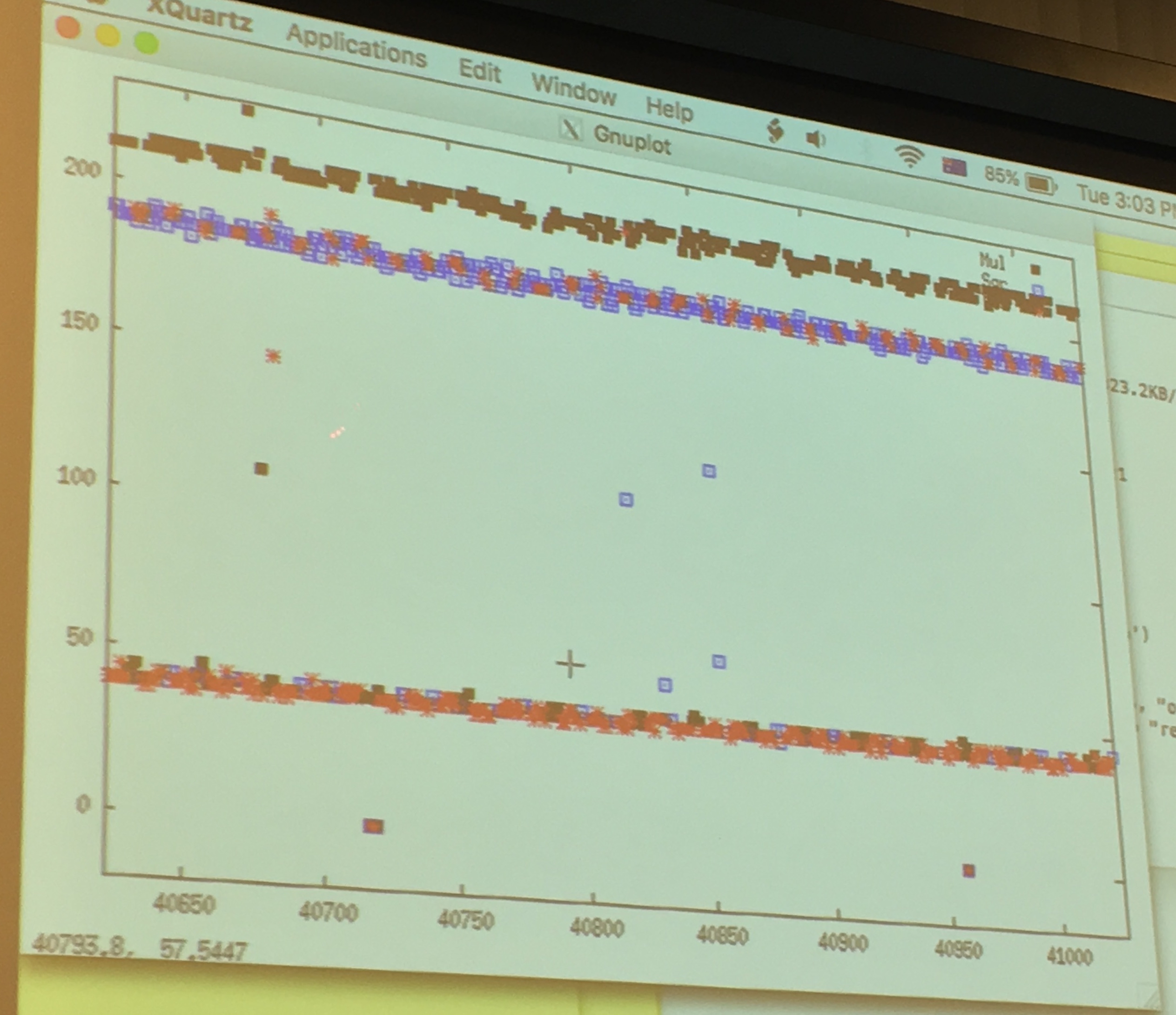
around the 50 line are the quick cache access, around the 200 line are the slow read from memory.

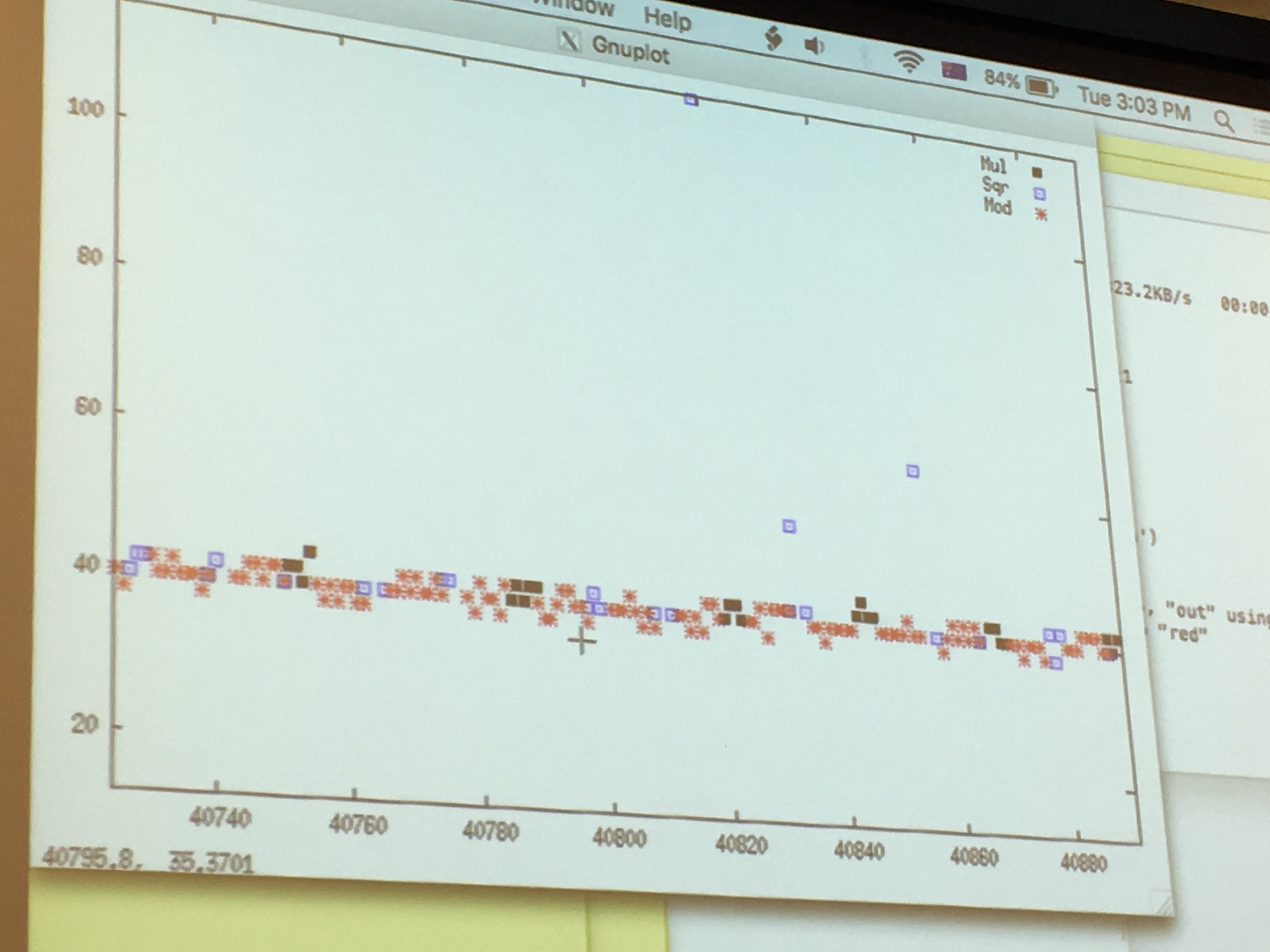
If we look only at the quick cache access, that are quick probably because the victim just had accessed it and loaded it into the cache before us, we can see that: red is the square operation, blue is the multiply operation and we can read out the key directly like a good ol' Simple Power Analyzis. There will be errors/noise of course, so run it several time! But even if you don't know all thebits, you can probably already break RSA.

There are some problems though:

There are also ways to improve the flush+reload attack:

It seems like the first trick slows down the victim by running a lot of processes in parallel. The second improvement flushes commonly used cache lines to slow down the victim as well.

Variants of this flush+reload attack exist:

• Evict+Reload uses cache contention instead of clflush, you replace the memory by loading something else instead of flushing it (naturally, flush happens rarely, eviction is what is really happening).
• Flush+Flush (same people as Flush+Reload). They realized that if we used flush on some data that was already in the cache it's slower, if we do the flush and the data is not cached it will be faster. But the error rate is increased so...
• Invalidate+Transfer, don't ask me about this one.

Now a new attack, Prime+Probe!

The attacker starts by choosing a block in memory, big enough so that it will cover all the cache, he then accesses that part of the memory to fill the entire cache with the attacker's data. You might want to fill parts of the cache that will be used by the victim's process as well. To do that you can trivially compute what will be the physical adresses mapped to your virtual cache.

After you filled the memory, you let the victim execute his process and access some places in memory to load it into the cache. This is evicting/removing some of the data that the attacker already loaded in the cache.

Now the attacker reads again the same block from memory and can see which parts have been removed because they take longer to load. By looking for patterns in there he can do another attack.

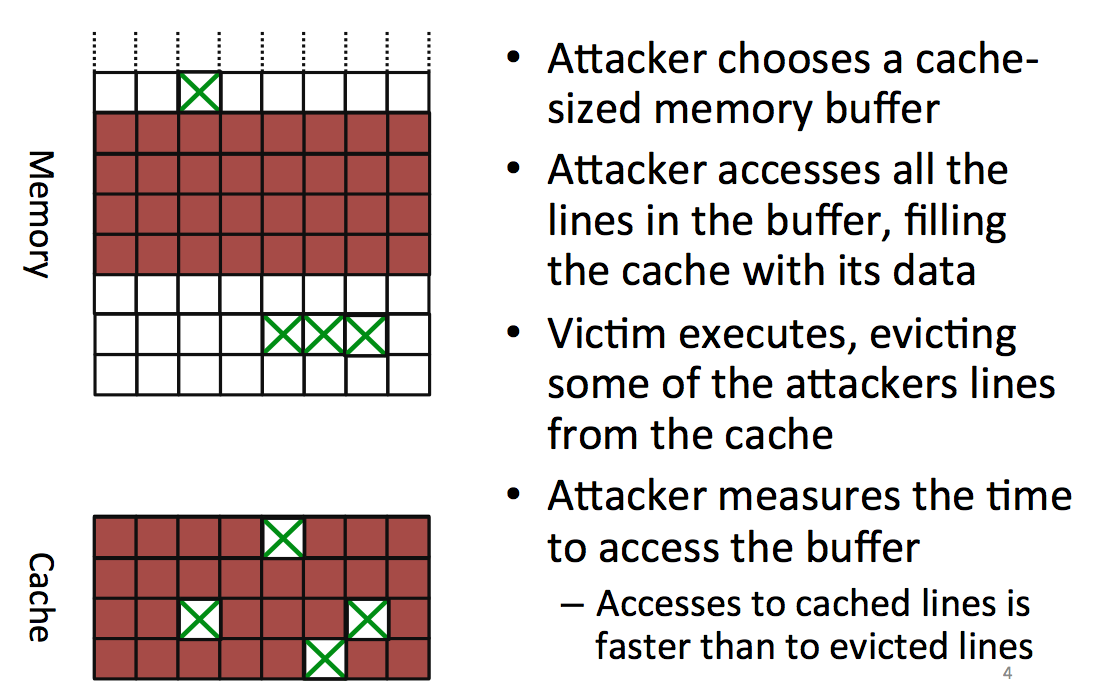
One problem: our code uses the cache as well! (here's the observer effect for you). Another problem: you can't write something useless to fill the cache, the compiler removes what he thinks is dead code/useless code (optimization). Here you need to know your compiler or... use assembly.

Thrashing is another problem that makes us miss victim's access.

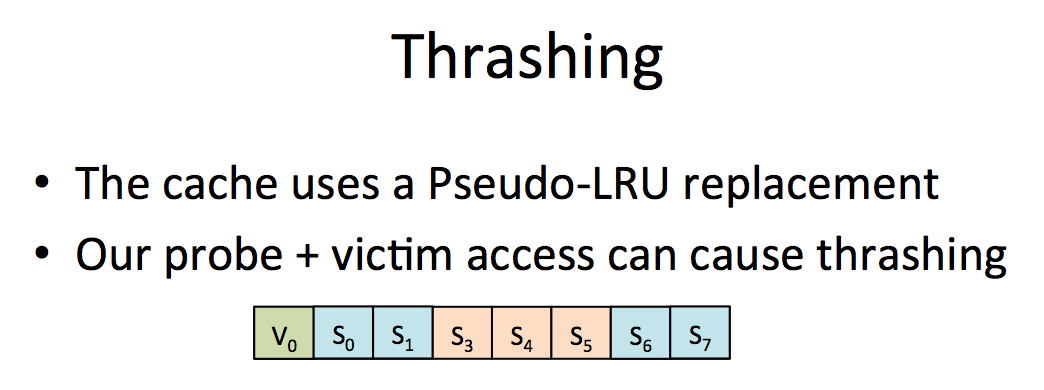
solution: zig zag on data. If someone knows what that means...

Another problem is Hardware prefetcher. The CPU brings data to the cache before it is being accessed (to optimize). The solution to that is to use pointer chasing: each future access depends on the previous one, so it kills any optimization of that sort.

Yarom demoed this. This time the tool was bigger. It's a L1 cache attack with L1-capture.c and L1-rattle.c. In L1, contrarily to flush+reload, we can monitor everything. So the default is to monitor everything. To do this attack you need to share a core with the process, which doesn't happen a lot, I'm not sure if you can do this attack on a shared cache. I don't see why not though, if someone can clarify...

Finally, Yarom presented some countermeasures to these kind of cache-timing attacks:

• don't share your hardware
• use hardware cache partitioning (intel cache allocation technology), this way you can decide in which way processes should have separated access in the cache.
• use cache randomisation instead of mirroring the memory.

At the system level, we can reduce the way we share memory. Of course if you don't share cores you avoid a lot of attacks, but you will need a lot of cores... Cache coloring is the idea of protecting certain places of the cache. There is also CATalayst and CacheBar...

On the software side, the big countermeasure is constant-time programming. Some blinding helps as well.

CHES 2016 tutorial part 1: Common Criteria Certification of a Smartcard: A Technical Overview posted August 2016

CHES started with a Tutorial on Smartcards, their certifications and their vulnerabilities. The morning was mostly a talk by Victor Lomné (ANSSI) about the Common Criteria for smartcards (CC), a framework through which smartcards vendors can make claims of security and labs can get them certified.

These certifications have different levels of security, from trivially testing the functionalities, to formally verifying them with the use of tools like COQ

What Gemalto, Obertur, and others... do is to buy an new security IC from a manufacturer and develop a semi-open platform with an OS (often a Javacard OS) then get that thing certified. After that their client (banks?) buys it, develop applications on it via SDKs and re-apply for a certification after that.

From what I got from both the whitebox and this workshop is that we actually don't know how to fully protect against side-channels attack and so we need to protect in hardware via anti-tampering and anti-observing measures.

To check the security of these physical thingies you need a lab with really efficient microscopes (atomic-force microscopy (AFM) or scanning electron microscope (SEM)), because chips are crazy smalls nowadays! Chemical tools to unsolder components, ...

All these tools cost a huge amount. Maintenance of the equipment is also another huge cost. You don't open a lab like that :)

Here are different goals of your attack, first you need to bypass these detectors, like canaries in "protected" binaries:

The labs do all these kind of attacks for every chips.

For lasers attack, they look at the power consumption, when they detect certain pattern it triggers the laser. These kind of tools are not really known by the academic community, but in the certification world it happens all the time.

In whitebox type evaluation (needed since it helps saving a lot of time), the evaluator knows the key already so that he can correctly debug his faults attacks, and verify as well the result of an attack.

Side channel attacks use power and electromagnetic stations. Basic techniques were they record traces, align them, apply known attacks...

Like other hardware thingies, they have "test features" (think JTAG). You can try to re-enter these test mode with faults and focused ion beams (FIB) and then you can dump the non-volatile memory (NVM)

Attacks on RNG exist as well. Basically when you can do fault attacks you can have fun =)

Attacks on the protocols as well...

the language used (javacard) also introduce new vulnerabilities. You can try to inject applets in the system to recover secrets, via a smartcard reader, you can try to escape from javacard via type confusion and other common vulnerabilities in javacard. It gets crazier than that by mixing in fault attacks modifying the purpose of current applets.

Another thing is that they need a large number of devices because fault attacks, especially lasers and FIBs, will often break the device.

Your certification is basically a score, it's calculated with some table. If the attack took more time, you get more points. If it took many experts instead of one, you get more points. If you had helping documents to help you, more points. If you needed to use many devices/samples to success at an attack, more points. Same for the cost of the equipment.

Victor gives an example of an fault attack on RSA. You do a fault attack on one part of the CRT, but then a verification is done at the end, so you need to do a fault attack on the verification as well. Now you need to find the correct timing to do these two laser shots. These spatial and temporal identifications take time. They also need open samples for that. Once they have the attack in place they need to try and perform it on a closed sample.

He also told us to watch this video:

You can read part 2 here