Quick access to articles on this page:
more on the next page...
I already wrote a lot about Disco:
Today, I released the white paper that introduces the construction. Check it out on ePrint.

It's a combination of everything I've talked about, plus:
- some experimental results on embedded devices done by Matteo Bocchi and Ruggero Susella
- some preliminary results on formal verification with Tamarin Prover
I unfortunately did not have the time to complete the formal verification of several important lemmas. But I am hopping that I can achieve this in a later paper. The formal verification code is on github and anybody is welcome to help :)
1. Bits and Their Encoding
Imagine that I generate a key to encrypt with AES. I use AES-128, instead of AES-256, so I need a 128-bit key.
I use whatever mechanism my OS gives me to generate a long string of bits. For example in python:
>>> import os;
>>> random_number = os.urandom(16)
>>> print(bin(int(random_number, 16))[2:])
11111010110001111100010010101111110101101111111011100001110000001000010100001000000010001001000110111000000111101101000000101011
These bits, can be interpreted as a large number in base 2. Exactly how you would interpret 18 as "eighteen" in base 10.
This is the large number in base 10:
>>> print(int(random_number, 16))
333344255304826079991460895939740225579
According to wolframalpha it reads like so in english:
333 undecillion 344 decillion 255 nonillion 304 octillion 826 septillion 79 sextillion 991 quintillion 460 quadrillion 895 trillion 939 billion 740 million 225 thousand 579.
This number can be quite large sometimes, and we can make use of letters to shorten it into something more human readable. Let's try base 16 which is hexadecimal:
>>> print(random_number.encode('hex'))
fac7c4afd6fee1c085080891b81ed02b
You often see this method of displaying binary strings to a more human readable format. Another popular one is base64 which is using, you guessed it, base 64:
>>> import base64
>>> print(base64.b64encode(random_number))
+sfEr9b+4cCFCAiRuB7QKw==
And as you can see, the bigger the base, the shorter the string we get. That is quite useful to keep something human readable and short.
2. Bytes and Bit-wise Operations
Let's go back to our bitstring
11111010110001111100010010101111110101101111111011100001110000001000010100001000000010001001000110111000000111101101000000101011
this is quite a lot of bits, and we need to find a way to store that in our computer memory.
The most common way, is to pack these bits into bytes of 8 bits (also called one octet):
11111010 11000111 11000100 10101111 11010110 11111110 11100001 11000000 10000101 00001000 00001000 10010001 10111000 00011110 11010000 00101011
As you can see, we just split things every 8 bits. In each bundle of 8 bits, we keep the bit-numbering with the most significant bit (MSB) first. We could have had the least significant bit (LSB) first instead, but since our larger binary string already had MSB first, it makes sense to keep it this way. It's also more "human" as we are used to read numbers from left to right (at least in English, French, Chinese, etc.)
Most programming languages let you access octets instead of bits directly. For example in Golang:
a := []byte{98, 99} // an array of bytes
b := a[0] // the byte represented by the base 10 number '98'
To act on a specific bit, it's a bit more effort as we need to segregate it via bitwise operations like NOT, AND, OR, XOR, SHIFTs, ROTATIONs, etc.
For example in Golang:
a := byte(98)
firstBit := a >> 7 // shifting 7 bits to the right, leaving the MSB intact and zero'ing the others
So far, all of these things can be learned and anchored in your brain by writing code for something like cryptopals for example.
3. Memory
OK. How do we store these octets in memory? Unfortunately, because of historical reasons, we have two ways of doing this:
- Big-Endian: from low memory address (00000....) to high memory address (999999...) in that order.
- Little-Endian: from high memory address (9999999...) to lower memory address (0000000...) in that order.
We call this Endianness.
I'm sorry, but to understand the rest of this article, you are going to have to parse this small snippet of C first:
#include <stdlib.h>
#include <stdio.h>
#include <stdint.h>
int main(){
uint8_t a[] = {1, 255}; // storing [1, 255]
printf("%p: x\n", a, *a); // 0x7ffdc5e78a70: 01
printf("%p: x\n", a+1, *(a+1)); // 0x7ffdc5e78a71: ff
}
As we can see, everything works as expected:
a points to an address in memory (0x7ffdc5e78a70) containing $1$- the next address (
0x7ffdc5e78a71) points to the value $255$ (displayed in hexadecimal)
The number 0x01ff (the 0x is a nice way to indicate that it is hexadecimal) represents the number $1 \times 16^2 + 15 \times 16^1 + 15 \times 16^0 = 511$ (remember, f represents the number 15 in hexadecimal).
So let's try to store that number in a different way in C:
#include <stdlib.h>
#include <stdio.h>
#include <stdint.h>
int main(){
uint16_t b = 0x01ff; // storing [1, 255] ?
//uint16_t b = 511 // these two lines are equivalent
uint8_t *a = (uint8_t*)&b; // getting octet pointer on b
printf("%p: x\n", a, *a); // 0x7ffd78106986: ff
printf("%p: x\n", a+1, *(a+1)); // 0x7ffd78106987: 01
}
Wait what? Why is the order of 01 and ff reversed?
This is because the machine I used to run this uses little-endianness to map values to memory (like most machines nowadays).
If you didn't know about this, it should freak you out.
But relax, this weirdness almost NEVER matters. Because:
- in most languages, you do not do pointer arithmetic (what I just did when I incremented
a)
- in most scenarios, you do not convert back and forth between bytestrings and number types (like
int or uint16_t).
And this is pretty much why most systems don't care too much about using little-endian instead of big-endian.
4. Network
Networking is usually the first challenge someone unfamiliar with endianness encounters.
When receiving bytes from a TCP socket, one usually stores them into an array. Here is a simple example in C where we receive a string from the network:
char *a = readFromNetwork() // [104, 101, 108, 108, 111, 0]
printf("%s\n", a); // hello
Notice that we do not necessarily know in which order (endianness) the bytes were sent, but protocols usually agree to use network byte order which is big-endian. This works pretty well for strings, but when it comes to number larger than 8-bit, you need to know how to re-assemble it in memory depending on your machine.
Let's see why this is a problem. Imagine that we want to transmit the number $511$. We need two bytes: 0x01 and 0x0ff. We transmit them in this order since it is big-endian which is the prefered network-byte order. On the other side, here is how we can receive the two bytes, and convert them back into a number type:
uint8_t a1[] = {1, 255}; // storing the received octets as-is (from left to right)
uint8_t a2[] = {255, 1}; // storing the octets from right to left after reversing them
uint16_t *b1 = (uint16_t*)a1;
uint16_t *b2 = (uint16_t*)a2;
printf("%"PRIu16"\n", *b1); // 65281
printf("%"PRIu16"\n", *b2); // 511
In this case, we see that to collect the correct number $511$ on the other end of the connection, we had to reverse the order of the bytes in memory. This is because our machine is little-endian.
This is what confuses most people!
In reality, it shouldn't. And this should re-assure you, because trying to figure out the endianness of your machine before converting a series of bytes received from the network into a number can be daunting.
Instead, we can rely on bitwise operations that are always emulating big-endianness! Let's take a deep look at this short snippet of code:
uint8_t* a[] = {1, 255}; // the number 511 encoded in network byte-order
uint16_t b = (a[0] << 8) | a[1];
printf("%"PRIu16"\n", b); // 511
Here, we placed the received big-endian numbers in the correct big-endian order via the left shift operation. This code works on any machine. It is the key to understanding why endianness doesn't matter in most cases: bit-wise operations are endianness-independent.
Unless your job is to implement low-level stuff like cryptogaphy, you do not care about endianness. This is because you will almost never convert a series of bytes to a number, or a number to a series of bytes.
If you do, because of networking perhaps, you use the built-in functions of the language (see Golang or C for example) and endianness-independent operations (like left shift), but never pointer arithmetic.
MIT Computer Science & Artificial Intelligence Lab just released some new research. The paper is called Vault: Fast Bootstrapping for Cryptocurrencies.
From a high level, it looks like a new cryptocurrency. But it is written as a set of techniques to improve Algorand and other cryptocurrencies are encouraged to adopt them, which leads me to think this will probably not become another cryptocurrency. It is very well written and I thought I would write a summary here.
After installing a cryptocurrency client, you usually sync it with the network in order to be able to participate or see the latest state of the blockchain. This whole concept of joining a cryptocurrency as a client is costly. For example, to join Bitcoin you need to download the whole blockchain which is more than 150 GB at the moment. It can take days and lot of bandwidth.
The whole point of Vault (the paper) is about reducing this bootstrapping process, and the space needed after to keep using the blockchain. It includes three techniques which I will briefly summarize below:
First technique: balance pruning.
Ethereum got rid of Bitcoin's UTXOs and keeps track of all the account balances instead. This method already saves a lot of space. Once you do that though, you are required to keep track of a nonce per account. This is to prevent transactions replay.
How does the Ethereum nonce works: when you sign a transaction, you also sign the nonce. Once it gets accepted in a block the nonce of your account gets incremented, and the next transaction will need to sign the new nonce to get accepted.
Vault doesn't keep a nonce, instead it tracks the hashes of all the transactions that were applied. This way, If you try to replay a transaction, it will be detected.
That's too costly though, we don't want to store ALL of the transactions ever. So the first technique is to force transactions to expire. Once a transaction is expired, a client can get rid of it in its storage, as it cannot be replayed (it is not valid anymore).
Another issue with Ethereum are zero-balance accounts.
Our analysis of the Ethereum state indicates that around 38% of all accounts have no funds and no storage/contract data (i.e., only an address and a nonce)
These zero-balance accounts still need to be tracked because of the nonce that is still useful to prevent future transaction replays.
In Vault, once all transactions applied on a zero-balance account have expired, you can prune the account.
This first technique allows a lot of useless data to be cleaned out. A client only stores accounts that have a balance greater than zero, zero-balance accounts if they still have transactions that could be replayed, and recent committed/pending transactions that haven't expired yet.
Second technique: balance sharding.
Keeping track of all the accounts is costly for one client... We can do better.
Vault uses a sparse Merkle tree where the leaves represent all the possible accounts.
It's quite a large tree... so we can split it in shards! The first $X$ bits of someone's public key could indicate what shard they should store. For example if we want to have 4 shards, the first 2 bits would indicate the path in the tree (0 is left, 1 is right).
Instead of storing all the leaves, you would store all the leaves that belong to your "subroot" (specified by the first bits of your public key).
By doing this we can't verify transactions anymore though...
To solve this, every transaction now ships with a proof of membership (a witness) for both the sender and recipient addresses.
This proof of membership is a typical merkle tree concept, it contains the neighbor nodes of the leaf's path up to the root as well as the leaf itself (account balance). This way anyone can verify a transaction!
Furthermore, once a transaction is committed to a block, the merkle tree is updated and its root are updated as well (because an account balance (a leaf) has changed).
So pending transactions in the mempool (the pool of pending transactions) need to have their membership proofs updated. Anybody has enough information to do this so it is not a problem. (By the way this is why transactions carry the recipient address' witness (the membership proof)l: because that leaf gets affected by a transaction as well.)
These two proofs are quite long though, and they accompany every transactions being broadcasted on the network!
One way to reduce that is to decrease the length of the membership proof. To do this, every client stores a level of subroots of the balance merkle tree, this way a proof doesn't need to go up to the root, but up to the level that the client has stored. The rest can be calculated from what is on disk.
Thanks to this second technique, one only needs to keep track of his own leaf (account balance) as well as the balance merkle root. And one can still verify new blocks. If one wants to help storing part of the network, one can keep track of a shard instead of the whole list of accounts.
I think the sharding thing here is actually less important than the transactions shipping with the balance proofs. But it is still a neat way of making sure that all nodes can participate in conserving the full blockchain and its balances.
Third technique: stamping certificates.
Vault is built on top of Algorand. The Algorand protocol is so elegant, I can see why they would want to make use of it.
Algorand's byzantime agreement BA* produces a "certificate" for each block committed to the blockchain. A certificate is a bundle containing more than 2/3rd signatures of the block from a randomly selected committee. Such a certificate is quite large (lots of signatures, public keys, and proof that the public key could participate in BA*). In addition, Algorand "mines" a new block every 2-3 seconds, so it has quite a large blockchain and a new client needs to download and verify a huge number of blocks to join the network.
To speed this up, Vault has nodes create additional "stamped certificates" at larger intervals (one every thousand blocks or so). From one stamped certificate, you can fast forward thousands of blocks ahead (~2 days of history) to the next stamped certificate. To create these stamped certificates, they use the same cryptographic sortition technique that Algorand uses but with a smaller number of participants to reduce the size of the stamped cert. (No, BLS and aggregate signatures won't help because as I've said a certificate contains a lot of distinct objects).
This way, to join the network, a client can validate blocks and certificates until it finds its first stamped certificate, then the client can jump thousands of blocks ahead from stamped certificate to stamped certificate until it reaches the most up-to-date block. There are more optimizations and details to it addressed in the paper.
I the end these stamped certificates are some kind of checkpoints. I find that it is not as elegant as Coda's protocol solution which only contains one zero-knowledge proof of the whole chain, but ZK-SNARKS being quite complicated I can see how one would want to avoid them.

BLS is a digital signature scheme being standardized.
Its basis is quite similar to other signature schemes, it has a key generation with a generator $P2$:
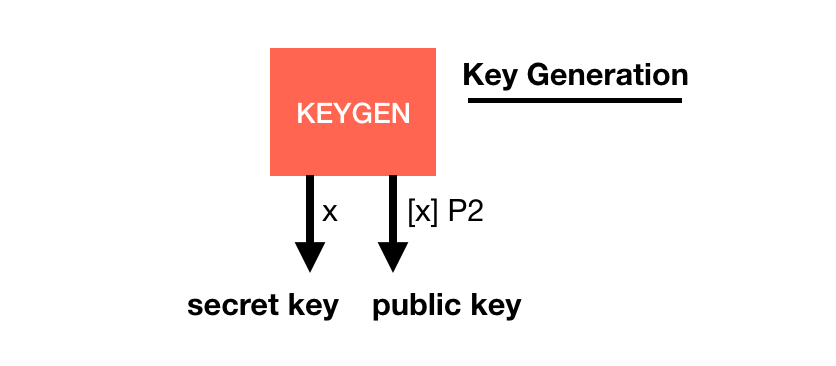
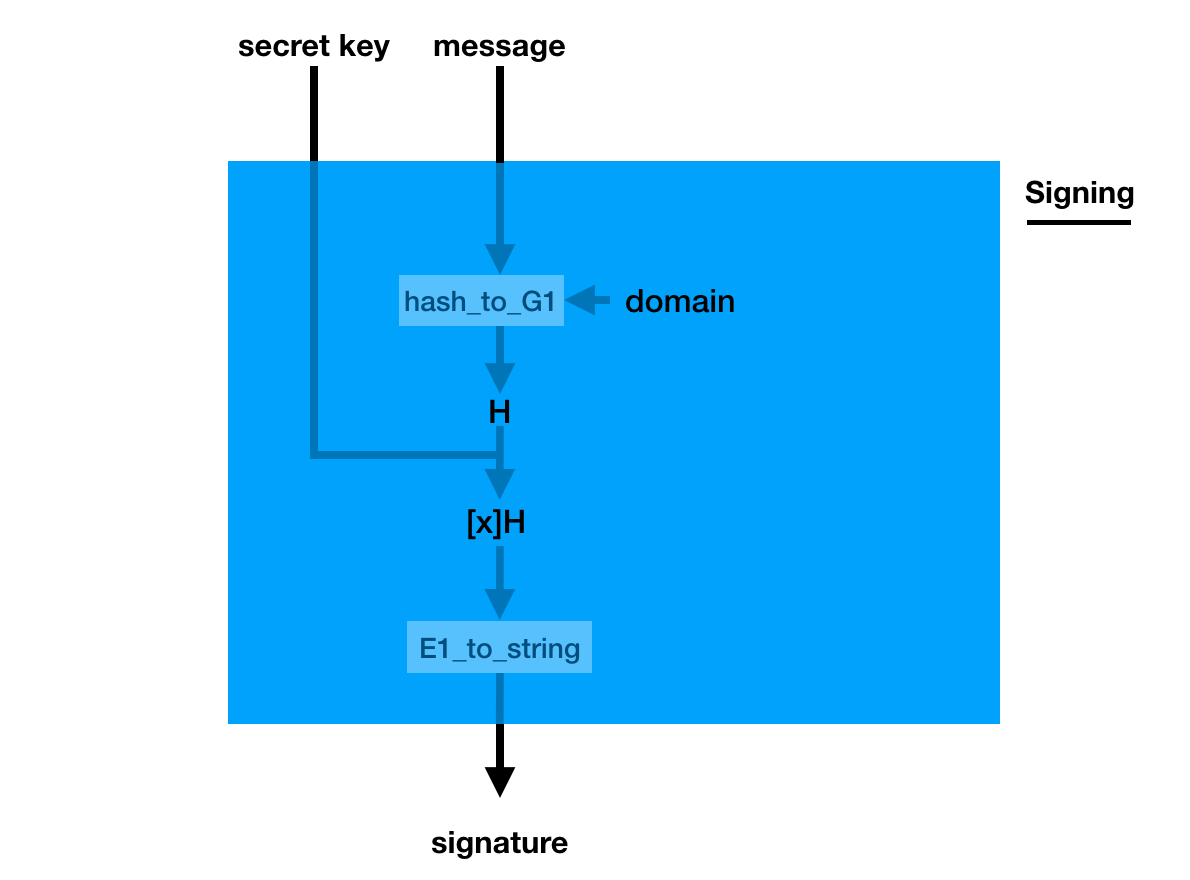
The signature is a bit weird though, you pretend the hashed message is the generator (using a hash_to_G1 function you hash the message into a point on a curve) and you do what you usually do in a key generation: you make it a public key with your private key
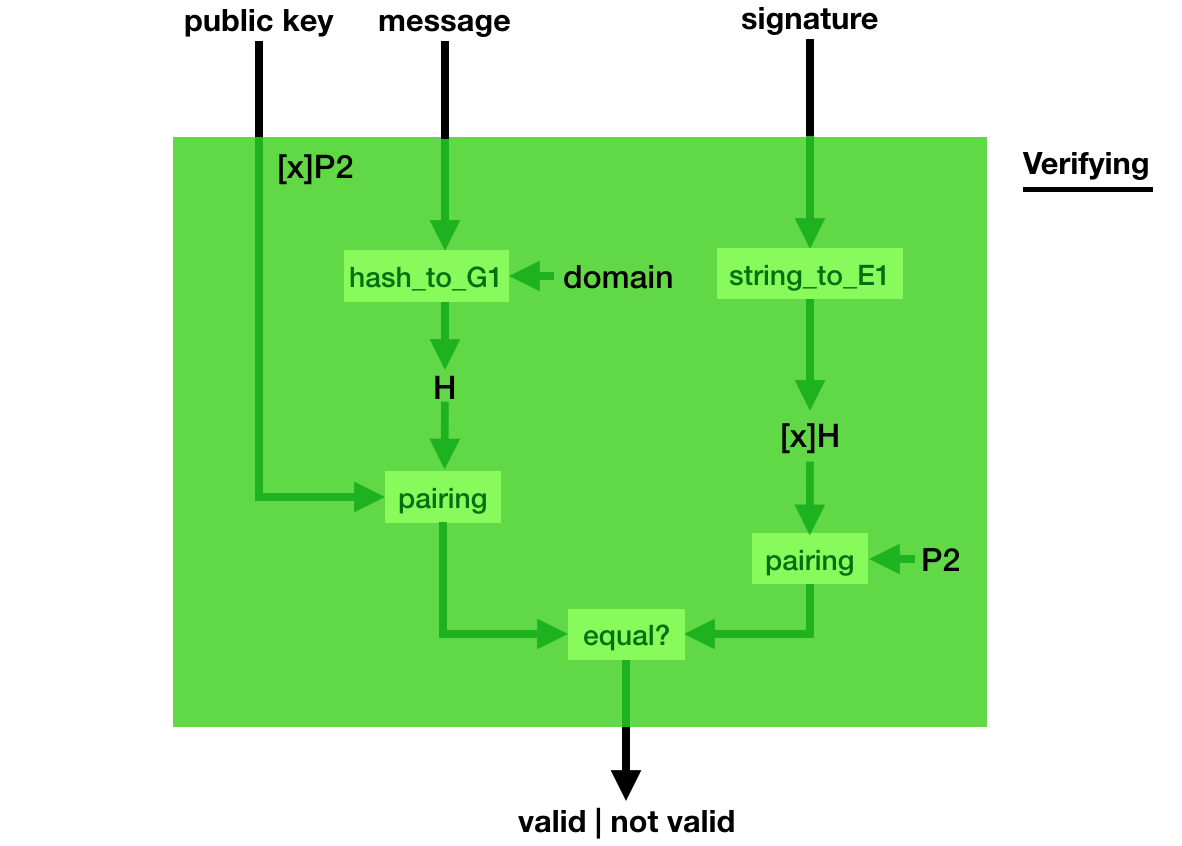
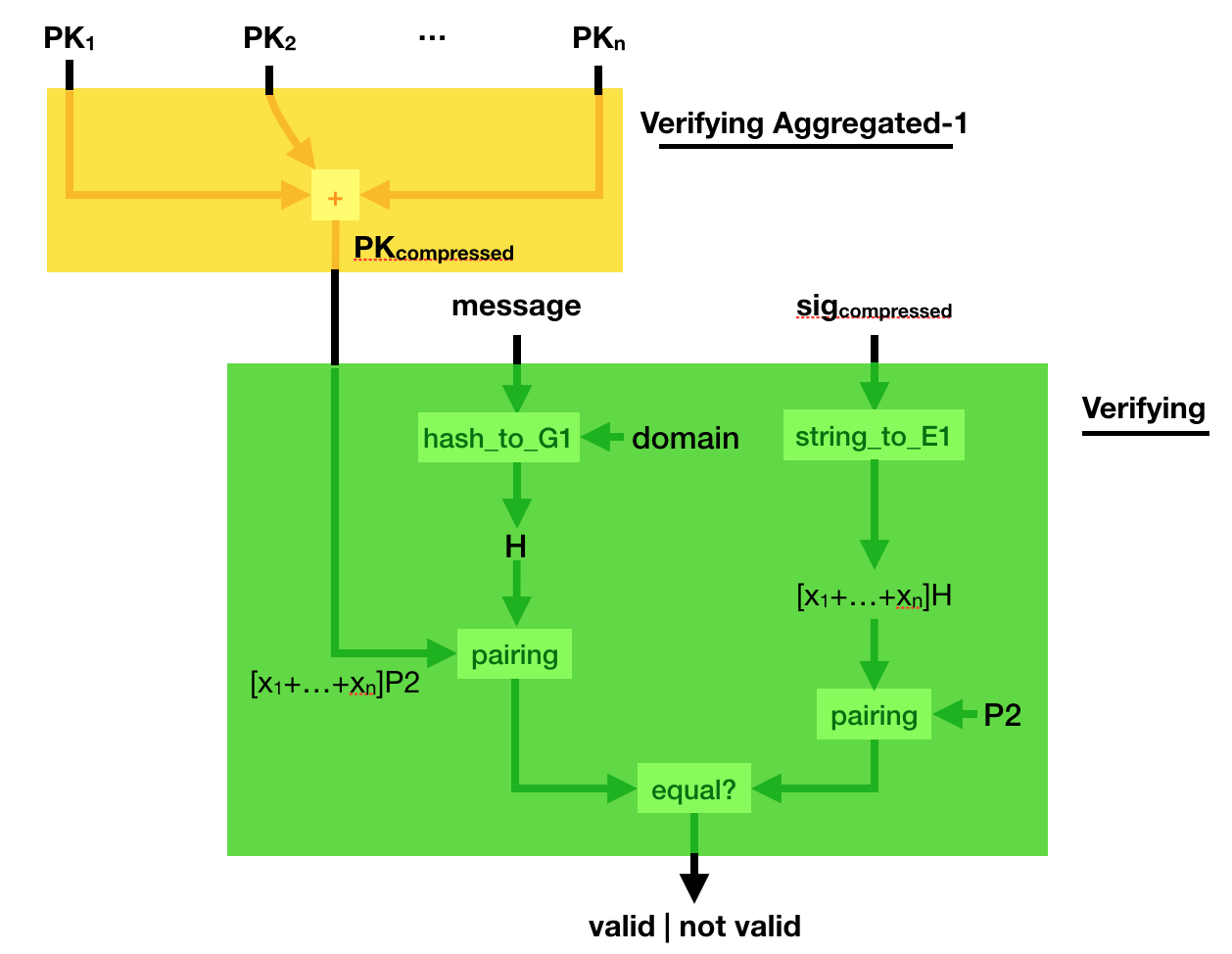
Verification is even weirder, you use a bilinear pairing to verify that indeed, pairing([secret_key]hashed_msg, P2) = pairing([secret_key]P2, hashed_msg).
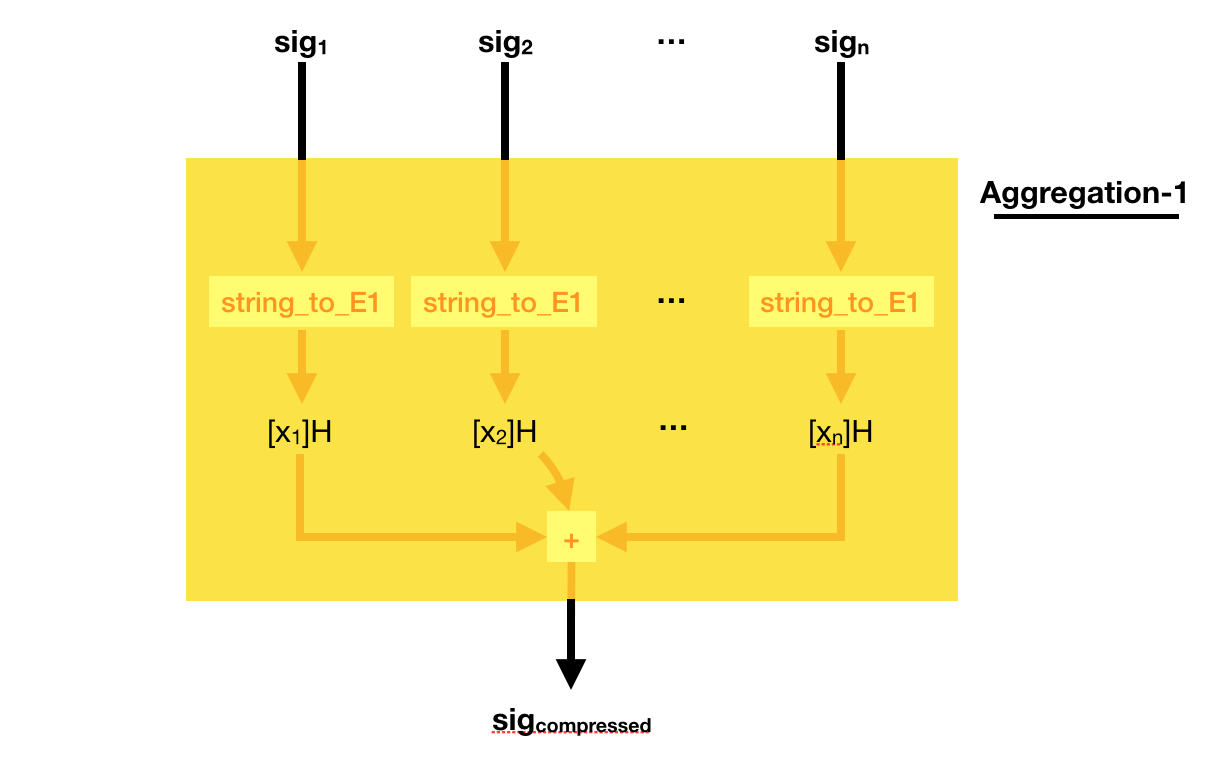
This weird signing/verifying process allows for pretty cool stuff. You can compress (aggregate) signatures of the same msg in a single signature!
To do that, simply add all the signatures together! Easy peasy right?
Can you verify such a compressed signature? Yes you can.
Simply compress the public key, the same way you compressed the signature. And verify the sig_compressed with the public_key_compressed. Elegant :)
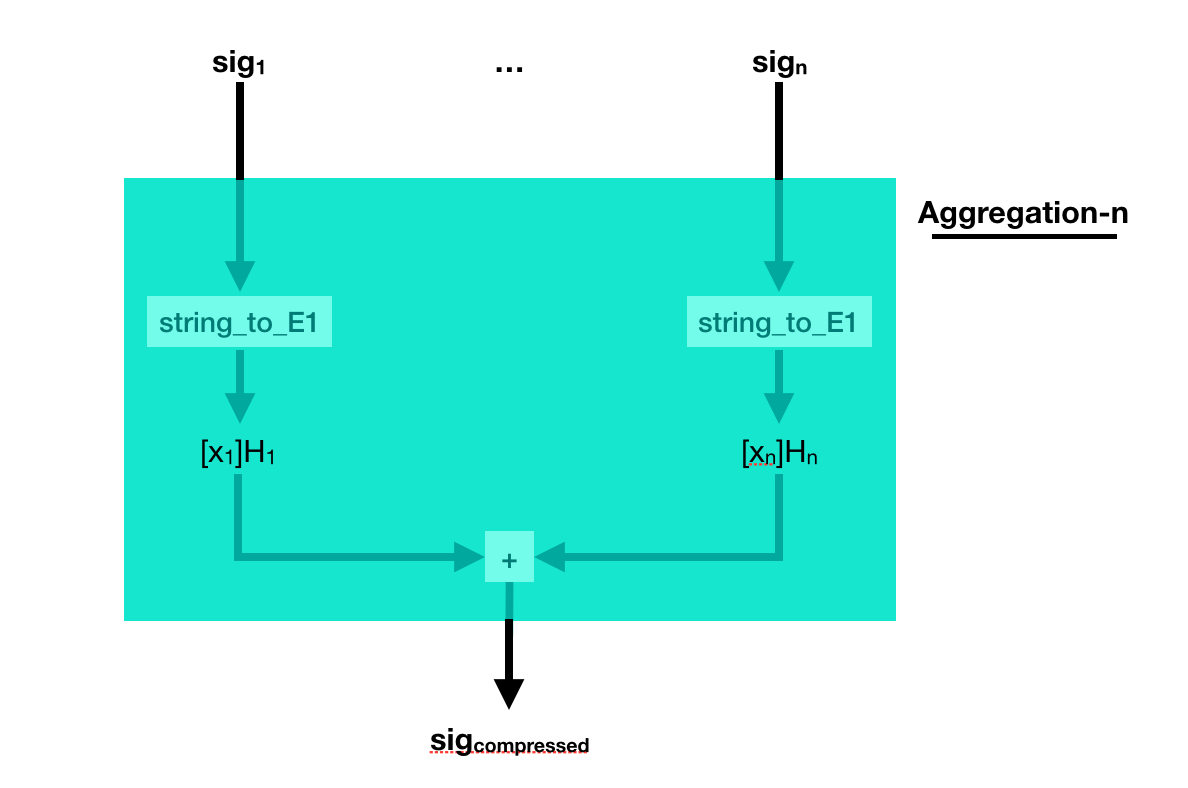
But what if the different signatures are on different messages? Well, just add them together as well.
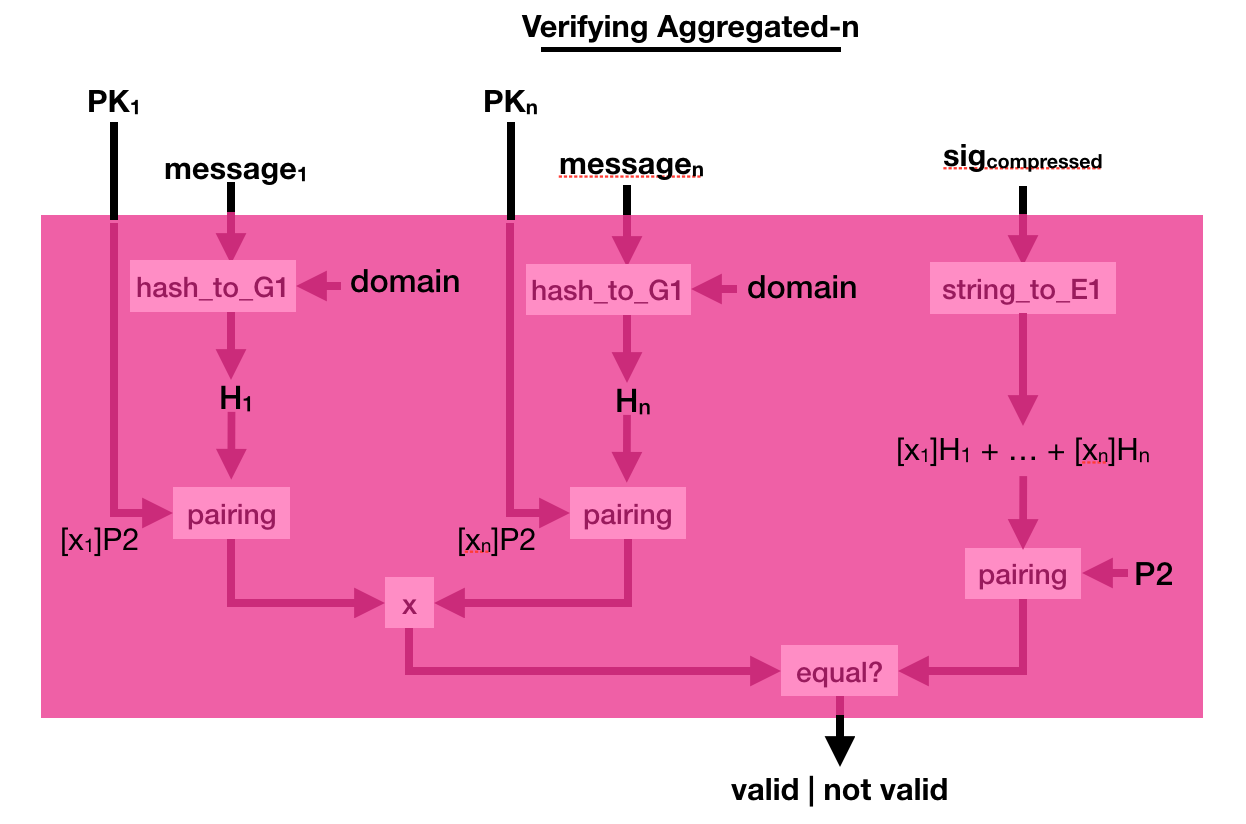
The process to verify that is a bit more complicated. This time you multiply a bunch of pairing([secret_key]P2, hashed_msg) together, and you verify that it is equal to another pairing made out of the compressed signature. Pairings are magical!
A paper on (attacking) database encryption was just released by Paul Grubbs, Marie-Sarah Lacharite, Brice Minaud, and Kenneth G. Paterson. Matthew Green just posted an article about it. I don't know much about database encryption, but from my experience there is a lot of solutions and it is quite hard to understand what you're getting from them. So I really like this kind of articles. I figured I would add my 2 cents to encourage people to write about database encryption.
Anonymity
I want to mention this first, because this is one of the most stupid solution I've seen being used to either anonymize a database or protect it. What you do is that you keep track of a mapping between real words and random words. For example "pasta" means "female" and "guitar" means "male". Then you replace all these words by their counterparts (so all the mention of "female" in your database get replaced by "pasta"). This allow you to have a database that doesn't hold any information. In practice, this is leaking way too much and it is in no way a good idea. It is called tokenization.
Database Breaches
Databases contain user information, like credit card numbers and passwords. They are often the target of attacks, as you can read in the news. For example, you can check on haveibeenpwned.com if your email has been part of a database breach. A friend of mine has been part of 19 database breaches apparently.
To prevent such things from happening, on the server side, you can encrypt your database.
Why not, after all.
The easier way to do this is to use Transparent Database Encryption (TDE) which a bunch of database engine ship by default. It's really simple, some columns in tables are encrypted with a key. The id and the table name are probably used to generate the nonce, and there's probably some authentication of the row or something so that rows can't be swapped. If your database engine doesn't support TDE, people will use home-made solutions like sqlcipher. The problem with TDE or sqlcipher, is that the key is just lying around next to your database. In practice, this seems to be good enough to get compliant to regulation stuff (perhaps like FIPS and PCI-DSS).
This is also often enough to defend against a lot of attacks, which are often just dumb smash-and-grab attacks where the attacker dumps the database and flees the crime scene right away. If the attacker is not in a hurry though, he can look around and find the key.
It's not that hard.
EDIT: one of the not so great thing about this kind of solution, is that the database is not really searchable unless you left some fields unencrypted. If you don't do searches, it's fine, but if you do, it's not so fine. The other solutions I talk about in this post also try to provide searchable encryption. They belong in the field of Searchable Symmetric Encryption (SSE).
Untrusted Databases
The solution here is to segment your architecture into two parts, a client who holds the key and an untrusted database. If the database is breached, then the attacker learns nothing.
I hope you are starting to realize that this solution is really about defense in depth, we're just moving the security somewhere else.
If both sides are breached, it's game over, if the client is breached an attacker can also start making whatever requests it wants. The database might be rate-limited, but it won't stop slow attacks. For password hashing, there have been hilarious proposals to solve this with security through obesity, and more serious proposals to solve this with password hashing delegation (see PASS or makwa).
But yeah, remember, this is defense in depth. Not that defense in depth doesn't work, but you have to frame your research in that perspective, and you also have to consider that whatever you do, the more annoying it is and the more efficient it will be at preventing most attacks.
Optimizations
Now that we got the setup out of the way, how do we implement that?
The naive approach is to encrypt everything client-side. But this is awful when you want to do complicated queries, because the server has to pretty much send you the entire database for you to decrypt it and query it yourself. There were some improvements known there, but there is only so much you can probably do.
Other solutions (cryptdb, mylar, opaque, preveil, verena, etc.) use a mix of cryptography (layers of encryption, homomorphic encryption, order preserving encryption, order revealing encryption, etc.) and perhaps even hardware solutions (Intel SGX) to solve the efficiency issue.
Unfortunately, most of these schemes are not clear about the threat model. As they do not use the naive approach, they have to leak some amount of information, and it is not obvious what attacks can do. And actually, if you read the research done on the subject, it seems like they could in practice leak a lot more than what we would expect. Some researchers are very angry, and claim that the situation is worst than having a plaintext database due to do the illusion of security when using such database encryption solutions.
Is there no good solution?
In practice, fully homomorphic encryption (FHE) could work to prevent the bad leakage we talked about. I don't know enough about it, but I know that there is no CCA2-secure FHE algorithm, which might be an issue. The other, more glaring, issue is that FHE is slow as hell. It could be practical in some situations, but probably not at scale and for this particular problem. For more constrained types of queries, somewhat homomorphic encryption (SHE) should be faster, but is it practical? Partial homomorphic encryption (HE) is fast but limited. The paillier cryptosystem, an HE algorithm, is actually used in cryptdb to do addition on ciphertexts.
Conclusion
The take away is that database encryption is about defense in depth. Which means it is useful, but it is not bullet proof. Just be aware of that.
Along the years, I've been influenced by many great minds on how to do research. I thought I would paste a few of their advice here.
Disregard.
That advice from Feynman’s Breakthrough, Disregard Others!
was really useful to me as I realized that I HAD to miss out on what was happening around me if I wanted to do research. It's quite hard nowadays, with all the noise and all the cool stuff happening, to focus on one's work. But it seems like Feynman had the same issues even before the internet was born. So that's one of the secret: JOMO it out (Joy Of Missing Out).
The word was “Disregard!”
“That’s what I’d forgotten!” he shouted (in the middle of the night). “You have to worry about your own work and ignore what everyone else is doing.” At first light, he called his wife, Gweneth, and said, “I think I’ve figured it out. Now I’ll be able to work again!” […]
Reading Papers.
That advice comes from Andrew Ng's interview:
"I don’t know how the human brain works but it’s almost magical: when you read enough or talk to enough experts, when you have enough inputs, new ideas start appearing."
and indeed. I've noticed that, after reading a bunch of papers, new ideas usually pop in my head and I'm able to do some new research. It actually seems like it is the only way.
Dedication.
Richard Hamming in "You and Your Research" wrote several good advice:
Let me start not logically, but psychologically. I find that the major objection is that people think great science is done by luck. It's all a matter of luck. Well, consider Einstein. Note how many different things he did that were good. Was it all luck? Wasn't it a little too repetitive? Consider Shannon. He didn't do just information theory. Several years before, he did some other good things and some which are still locked up in the security of cryptography. He did many good things.
You see again and again, that it is more than one thing from a good person. Once in a while a person does only one thing in his whole life, and we'll talk about that later, but a lot of times there is repetition. I claim that luck will not cover everything. And I will cite Pasteur who said, ``Luck favors the prepared mind.'' And I think that says it the way I believe it. There is indeed an element of luck, and no, there isn't. The prepared mind sooner or later finds something important and does it. So yes, it is luck. The particular thing you do is luck, but that you do something is not.
Sam Altman wrote "compound yourself" the other day, which reflects what Hamming was saying as well when quoting Bode:
What Bode was saying was this: ``Knowledge and productivity are like compound interest.'' Given two people of approximately the same ability and one person who works ten percent more than the other, the latter will more than twice outproduce the former. The more you know, the more you learn; the more you learn, the more you can do; the more you can do, the more the opportunity - it is very much like compound interest
Mental State.
Here's some quote about being in the right state of mind. From Hamming again. The first one rings true to me as I gained much more confidence in doing research after releasing a few papers and being cited.
One success brought him confidence and courage
The second one is quite impactful as well, as trains, planes and hotels without wifi are often my most productive places to work from:
What most people think are the best working conditions, are not. Very clearly they are not because people are often most productive when working conditions are bad
It even sounds like prison, yes prison, is sometimes cited as the best place to do one's work! This is an extract of a letter from André Weil after having spent some time in Rouen's prison:
My mathematics work is proceeding beyond my wildest hopes, and I am even a bit worried - if it's only in prison that I work so well, will I have to arrange to spend two or three months locked up every year?
And if you can't believe this, here's what Reddit has to say about it:
Just spent four months in jail. I read over thirty books and I feel like I’ve been born again.
Important Problems.
Hamming again, on working on important problems:
And I started asking, "What are the important problems of your field?" And after a week or so, "What important problems are you working on?"
If you do not work on an important problem, it's unlikely you'll do important work. It's perfectly obvious. Great scientists have thought through, in a careful way, a number of important problems in their field, and they keep an eye on wondering how to attack them
I noticed the following facts about people who work with the door open or the door closed. I notice that if you have the door to your office closed, you get more work done today and tomorrow, and you are more productive than most. But 10 years later somehow you don't know quite know what problems are worth working on; all the hard work you do is sort of tangential in importance. He who works with the door open gets all kinds of interruptions, but he also occasionally gets clues as to what the world is and what might be important.
One's limitations.
Silvio Micali gave a talk in which the last 10 minutes (which I linked) were a collection of advice for young researchers. It's quite fun to watch and emphasizes that one must be stubborn to go through with one's research. He also mentions being fine with one's limitations:
Our limitation is our strength. Because of your limitation you are forced to approach a problem differently.
Maker's schedule.
Paul Graham wrote "Maker's schedule, manager's schedule" which differentiates the kind of work schedule one can have:
When you're operating on the maker's schedule, meetings are a disaster. A single meeting can blow a whole afternoon, by breaking it into two pieces each too small to do anything hard in. Plus you have to remember to go to the meeting. That's no problem for someone on the manager's schedule. There's always something coming on the next hour; the only question is what. But when someone on the maker's schedule has a meeting, they have to think about it.
This is something Hamming touched as well, but more on the personal life plan:
"I don't like to say it in front of my wife, but I did sort of neglect her sometimes; I needed to study. You have to neglect things if you intend to get what you want done. There's no question about this."
Deadlines.
I can't remember where I read that, but someone was saying that deadlines were great, and that he/she was often promising things to people in order to get things done. The idea was that if you break your promise, you lose integrity and shame rains upon you. So that's some sort of self-fabricated pressure.
More?
If you know more cool articles and videos like that, please share :)
At Real World Crypto 2019, Mihir Bellare won the Levchin Prize (along with Eric Rescorla) and gave a short and inspiring speech. You can watch it here. In it, he briefly mentioned what I'll call the speed issue:
when I started it was a question of being responsive to the industry and practical needs [...] Now I think these are much deeper questions [...] Who benefits from the work we do? [...] Who benefits from making things faster beyond a certain point? The constant search for speed. What sort of people do we become when we cannot wait half a second for a web page to load because TLS is doing a round trip and we're cutting corners.
In here, Bellare is obviously hinting at Eric Rescorla's work with TLS 1.3, in particular the 0-RTT or early data feature of the new protocol. If you don't know what it is, it's a new feature which allows a client to send encrypted data as part of its very first flight of messages. As I explained in this video, it does not protect against replay attacks, nor benefits from forward secrecy.
Replay: a passive observer can record these specific messages, then replay them at a later point in time. You can imagine that if the messages were bank transactions, and replaying them would prompt the bank to initiate a new transaction, then that would be a problem.
Forward Secrecy: TLS sessions in TLS 1.3 benefits from this security property by default. If the server's long-term keys are stolen at a certain point in time, previous sessions won't be decryptable. This is because each session's security is augmented by doing an ephemeral key exchange with keys that are deleted right after the handshake. To break such a session you would need to obtain these ephemeral keys in addition to the long-term key of the server. Sending 0-RTT data happens before any ephemeral key exchange can happen. The data is simply encrypted via a key derived from a pre-shared key (PSK). Here the lack of forward secrecy means that if the PSK is stolen at a later point in time, that data will be decryptable. This is much less of an issue for browsers as these PSK are often short-lived, but it's not always the case in other scenarios.
0-RTT has been pretty controversial, it has generated a lot of discussion on the TLS 1.3 mailing list (see 1, 2, 3) and concerns about its security have taken an entire section in the specification itself.
While I spent quite some time telling you about TLS 1.3's 0-RTT in this post, it is just one example of a security trade-off that WE made, all of us, for the benefit of a few big players. Was it the right thing to do? Maybe, maybe not.
What are the other examples? Well guess why we're using AES-GCM? Because it is hardware accelerated. But who asked Intel for it? Why are we standardizing a shitty WPA 3.0 protocol? Probably because some Wi-Fi Alliance is telling us to use it, but what the F is going on there? Why is full disk encryption (FDE) completely flawed? I am not even talking about the recent Self-encrypting deception: weaknesses in the encryption of solid state drives (SSDs) research, but rather the fact that vendors implementing FDE are never using authentication on ciphertexts! and continue to refuse to tackle the issue via primitives like wide-block ciphers. Probably because it's not fast enough!
Now look at what cryptographic primitives people are pushing for nowadays: AES-GCM, Chacha20-Poly1305, Curve25519, BLAKE2. This is pretty much what you're forced into if you're using any protocol in 2019 (yes even the Noise Protocol Framework). Are these algorithms bad? Of course not. But they are there because large companies wanted them. And they wanted them because they were fast. I touched on that in Maybe you shouldn't skip SHA-3 after Adam Langley's wrote an article on SHA-3 not being fast enough.
We're in a crypto era where the hotness is in the "cycles per byte" (cpp).
All of this is concerning, because once you look at it this way, you see that big players have a huge influence over our standards and the security trade-offs we end up doing for speed are not always worth it.
If you're not a big player, you most likely don't care about these kinds of optimizations. The cryptography you use is not going to be the bottleneck of your application. You do not have to do these trade-offs.
Mathias Hall-Andersen, Alishah Chator, Nick Sullivan and I have released a new construction called nQUIC.
nQUIC = Noise + QUIC
If you don't know what QUIC is, let me briefly explain: it is the last invention of Google, which is being standardized with the IETF. It's a take on the lessons learned developing HTTP/2 about the limitations of TCP. You can see it as a better TCP(2.0) for a better HTTP(/3) with encryption built in by default.
The idea is that, when you visit a page, you end up fetching way more files than you think. There is some .css, some .js, a bunch of .png and maybe even other pages via some iframes. To do this, browsers have historically opened multiple TCP connections (to the same server perhaps) in order to receive the file faster. This is called multiplexing and it's not too hard to do, you just need to use a different TCP port for every connection you create. The problem is that it takes time for each TCP connection to start (there is a TCP handshake as well as a TLS handshake) and then to figure out how fast they can go (TCP flow control).

So in HTTP/2, instead of opening several TCP connections to the same server, we just open one. We then do the multiplexing inside of this one connection.

So now you're doing one TCP handshake, then you optimize the connection via TCP's mechanism, and you rely on that to receive whatever the server sends to you. It sends you a bunch of blocks, in whatever order, that you can buffer and glue back together. For example, you might receive some html, then some jpg, then the rest of the html.
One problem is that if faults start appearing on the network, all the different objects you're trying to receive will be impacted, not just one of them. So one ACK can mess every element on the page.
Comes QUIC which fixes these multiplexing issues by re-inventing TCP. Because of middle boxes and firewall issues, QUIC is built on top of UDP instead of creating another protocol on top of IP. It doesn't matter much in theory because UDP is just IP with ports (and ports are useful).
QUIC has different streams, which can carry different content (in order) and are not impacted by issues happening in other streams. You can thus carry the html page in one stream, an image in another stream, the css file in another stream, etc.
On top of that, the people at Google thought that encryption would be very useful to have baked into the protocol instead of making it optional and a responsability of applications (that's what TLS is). Google started this encryption mechanism with QUIC Crypto, which was a very simple protocol, and then decided to replace it with TLS 1.3. While this might make sense for the web, it doesn't really make sense in other settings where simpler security protocols could be used. This is what I talked about in more length in this blog post. Go read it before reading the rest of this post, I'll wait.
You read it? Nice. Well you'll be delighted to see that the nQUIC I've talked about in the first line of this article is exactly what I've been talking about: QUIC secured by the Noise Protocol Framework instead of TLS 1.3.
You can read about the research here. What we found is that it is extremly easy to integrate Noise into QUIC, because it was made to be encapsulated into a lower protocol, whereas integrating TLS 1.3 into QUIC is very hackish. It is also faster, because of the lack of signatures. It is way more secure, thanks to the lack of complexity and x509 parsing as well as the symbolic proofs provided by the research community (see for example NoiseExplorer, and its wonderful talk at Real World Crypto 2019). Finally, we have also added post-compromise security to the protocol, which is a must for long-lived sessions.










