Quick access to articles on this page:
more on the next page...
As some of the readers of this blog know, I worked for two years at Novi (Facebook) on the Diem (formerly known as Libra) cryptocurrency. The project was recently dismantled, most likely due to regulator unwillingness to help a non-government backed cryptocurrency reach millions of people at scale.
Today, a group of 17 ex Novi/Diem engineers and researchers announced Aptos, presumably a fork of Diem. From what I understand, this means that a state-of-the-art blockchain that has been pushing the envelop in terms of innovation, security, and performance, and that's been in development for the last 4 years, now has a path to launch.
I'm guessing that we're going to see the typical proof-of-stake approach being implemented (unlike Diem's proof of authority) as well as a revamped set of smart contracts (written in Move) to govern the new blockchain. Besides that, the blockchain was already in a solid shape a year ago so I don't foresee any major changes.
Congratulation to the new team :) this is exciting.
Over 90 WordPress themes, plugins backdoored in supply chain attack
(source: bleepingcomputer.com)
A product can be seen as a production line. That's what The Phoenix Project novel argues. It makes sense to me. Things gets assembled and passed around, work stations can become bottlenecks, and at the end of the line you deliver the product to the user. In that production line, pieces come from your own warehouse, or from external vendors. That distinction my friend, is what we call "insider threat vs supply chain attacks" in security.
Insider threat is a problem that's mostly ignored today. Large corporations have spies in them, that's a given. They have poor ways to deal with them, but that's fine, because most of these spies are working from other governments and they're tolerated in the grand scheme of things. They might inject backdoors here and there (see the juniper incident) but most of the times they remain unnoticed and unproblematic.
Supply chain attacks, on the other hand, are from less sophisticated attackers. They're from script kiddies, blackhats, "hackers", and others that we generally don't label much as advanced (like in advanced persistent threat). But they are getting more and more advanced.
To counter supply chain attacks, the first thing you can do is inventory (some people might call this threat modeling). The idea, really, is to list all of the pieces and the flows that make up your product. An acyclic directed graph of machines and humans. Once you have that, it's much clearer what the different attack vectors are.
I'm a software person, so I mostly focus on software security. When you write software, you worry about a few things:
- your dependencies
- the flows around your code evolution
- what goes into a release
- how that release gets into production
The fourth point is sort of an infra problem, so it's not the most urgent problem you should think about as a developer. I'd say the third point could be an infra problem as well, unless you're lucky enough to have release engineers or dev infra people working in your company. The second point is probably Github, and all the corner cases you have around it. For the most part, you can choose to trust Github. The first point, the dependencies you're using, that is your problem.
I learned a few things, back at Facebook when I was working on libra/diem, and I think that could be useful to others. First, not languages are created equal. Languages like Golang are fantastic because they provide a rich standard library. What some would call a battery-included stdlib. Thanks to that, you rarely see Golang projects depend on more than 100 transitive dependencies (this means that I'm including dependencies that are used by your direct dependencies, and so on). Other languages, like javascript and Rust can have their dependency graph just blow up due to poor standard libraries and great package managers.
When I looked at what we were doing at the time with libra/diem, I got obsessed with the large amount of dependencies that our software used. A year in, I got inspired by Feymann's story about investigating the challenger disaster, and the way he managed to pinpoint the problem by using the wisdom of the crowd.
The wisdom of the crowd is this concept where the average of all people's guesses to a question can be extremely close to the real answer. The best demonstration to this concept is when a bunch of people are asked to estimate the number of jelly beans contained in a jar. Check that video on youtube. If you're french, fouloscopie is a great youtuber who does research about crowds and their behavior.
So I used the same methodology. I created a form and sent it to all the engineers at the company. The form asked the following: "for each pieces of our big puzzle, what is your estimation of the risk from 0 to 5? If you don't know leave it blank." The result was eye opening. The trivial parts were deemed not risky, as expected. The confusing parts (like consensus and HSM code) had estimations that were all over the place. Dependencies were ranked as the highest risk. Finally, some other parts that I had overlooked got ranked as high-risk which made a lot of sense and changed our strategy for the rest of the year.
So dependencies were definitely a problem, people agreed. What could we do? First, I developed a tool called dephell that would allow us to get some quick stats on the dependencies we were using in our Rust project. The tool was a bit buggy, and incorrect at times, but it was good enough to show us outliers. We used it on every libraries in our project to get a sense of what dependencies they were relying on. We had hundreds and hundreds of dependencies, so that was quite a hard task, but a few patterns stood out.
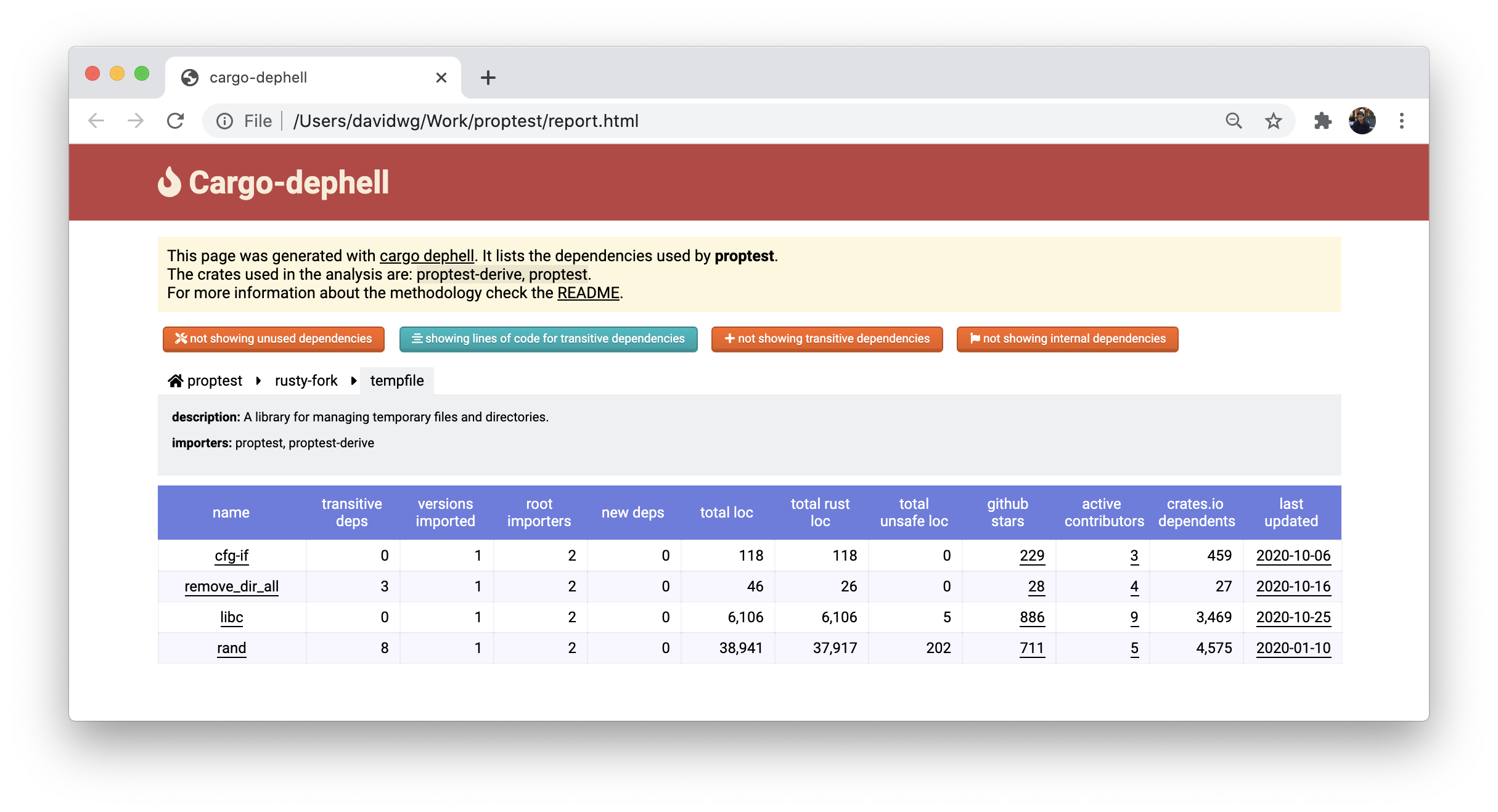
Sometimes, we used many different dependencies to solve the same problem. The fix was easy: decide which one was the most solid dependency and use that one. Other times, we would use a large dependency, that would import more dependencies, and notice that if we would rewrite it ourselves we could live with a much smaller amount of code and no dependencies. This is what I did when I wrote libra's noise implementation which removed a large amount of code and a few dozens of dependencies to a few hundreds of lines of code. Sometimes, we realized that the dependencies we were using were not great: they were not maintained, had unknown maintainers and contributors, lots of unsafe code, and so on. Finding a better alternative was usually the way to go.
That analysis got us to remove a lot of dependencies. But dependencies continue to creep in, and so we needed a flow to prevent that growth. The obvious solution was to add friction to the process of adding a dependency. Making sure that I was involved in accepting any PR that added a new dependency (via continuous integration) was enough. Most of the times it would go like this:
- hey! Can I get a review from you for this PR, it looks like you need to look at it since I'm adding a new dependency.
- for sure! I looked at the dependency and it's adding X lines of code, as well as Y additional dependencies. Is this something that's really necessary? Are there better alternatives?
- hum... actually I could write that in a few lines of code, let me try that instead.
At that point, you're having a good sense of what your dependencies are, you sorted them out and even did some cleaning, and you stopped the growth. You still have problems: dependencies evolve. We know, from experience, that the risk of not updating dependencies is higher than updating. That's because a lot of your updates will be bug fixes. So you need to update. Updating adds a few non-negligible risks though:
- a backdoor could have been introduced in a (transitive) dependency
- new dependencies could be added by the update
- new bugs could be introduced by the update
The cost of 3 is negligible compared to the bug fixes. Remember: you can't review every dependencies you're using. You wouldn't be using third-party dependencies in the first place if you had all the time in the world. 2 has to be taken into account in your dependency growth control strategy. 1 is the subject of this post.
To tackle 1, John and I created whackadep. Whackadep is a service, with a web UI, that monitors your repository. Originally architected to be language-agnostic, it was for obvious reasons built primarily for Rust codebases.
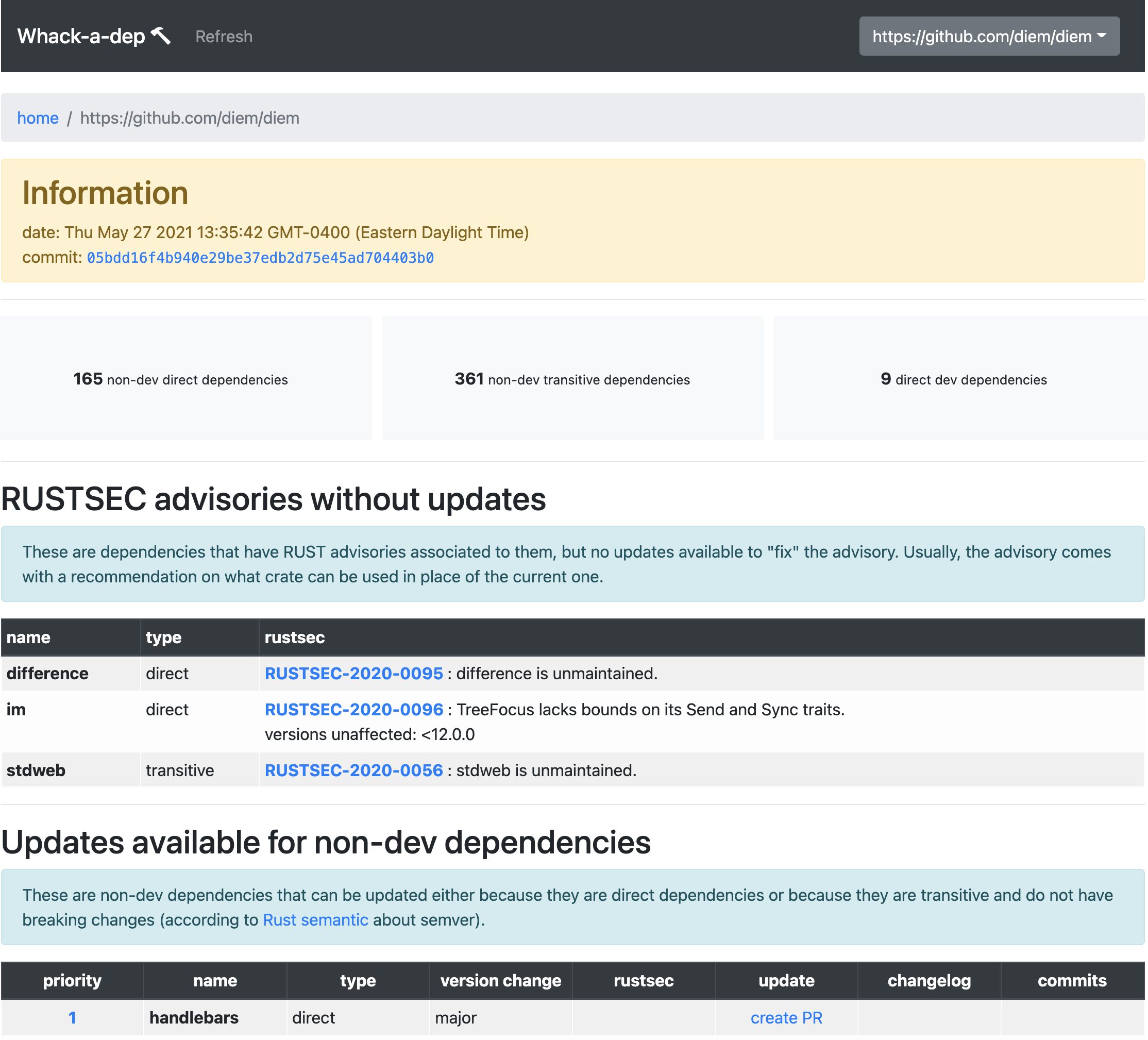
Whackadep's role was to periodically check if new updates were available, and to quickly show you two things:
- what was the risk of not updating
- what was the risk of updating
The risk of not updating is generally calculated via the help of RUSTSEC, the RustSec Advisory Database, as well as a calculation of the difference between the semantic versions. If the update is X breaking versions on top of your version, then it'll be harder to update if they're a serious bug that needs urgent fixing. All of this was taken into account to calculate a priority score that would help a human user figure out what to do.
The risk of updating was calculated from a few heuristics, but was meant to be extendable. The presence of an updated build.rs file, for example, was a big red flag. The presence of a new, never-seen-before, contributor in a release was also seen as a red flag. A number of these customizable heuristics would be used to calculate a risk score, which could be used by the user of the tool to decide if that warranted a human review.
Of course, in Rust-land, you get dependency updates every single day. So you need more reassurance that a review is not needed. For this, we came up with the idea of a trusted set of libraries. As Linus said one day (although I can't find that quote anymore): security works via a network, and if you don't do security via a network you're dumb. He said it sort of like that I believe. The idea is that you can't do everything yourself, and the only way to scale is to trust others. Thus, by whitelisting a number of libraries as being part of a club of well-maintained libraries with well-known authors, we could reduce the burden of reviewing dependencies.
Anyway, the whole point of this article is to show you that dependencies are a huge problem in most software stacks, and that solutions don't really exist to deal with this. Human processes are doomed to fail, and thus you need an automated and machine-built component to help you there. Interestingly, I just finished reading Zero to One a few days ago, and in the book Peter Thiel makes the point that machines shouldn't try to replace humans but instead provide services to help make them superheroes. This is what whackadep was aiming to do: give developers super powers. I hope I inspired some of you to continue pursuing this idea, because we're going to need some help.

(photo by @micheile)
Zkapps (formerly known as snapps) are zero-knowledge smart contracts that will launch on Mina this year. You can learn more about them here. This tutorial teaches you how to write a tic-tac-toe game using snarkyjs, the official library to write zkapps on Mina.
Set up
You can quickly create a project by using the Snapp CLI:
$ npm install -g snapp-cli
$ snapp project my-proj

you can also follow along this tutorial with the following command:
$ snapp example tictactoe
Hello world
To write a smart contract, import what you need from snarkyjs and simply extend the SmartContract class.
import {
Field,
State,
PublicKey,
SmartContract,
state,
method,
PrivateKey,
UInt64,
Int64,
Bool,
Circuit,
Mina,
Party,
shutdown,
Optional,
Signature,
} from 'snarkyjs';
class TicTacToe extends SmartContract {
// your smart contract
}
A zero-knowledge smart contract, or zkapp, is very close in concept to the ones you see on Ethereum:
- it has a state
- it has a constructor that initializes the initial state when you deploy your zkapp
- and it has methods that can mutate the state
Let's start with the state.
A state for a tic-tac-toe
Zkapps, at the lowest level, only understand field elements, of type Field. Field is a type similar to Ethereum's u256 except that it is a bit smaller. Essentially it's a number between 0 and 28948022309329048855892746252171976963363056481941560715954676764349967630336. Every other type has to be derived from Field, and we provide a number of such helpful types in snarky. (You can also create your own types but we won't use that here.)
First, a tic-tac-toe game needs to track the state of the game. The board.
The state of a zkapp can only hold 8 field elements. This is not set in stone, but the more storage a zkapp can contain, and the harder it becomes to participate in consensus (and thus the less decentralized the network becomes). Zkapps that need to handle large state can do so via Merkle trees, but I won't be talking about that here.
A tic-tac-toe board is made of 9 tiles, that's one too many :( so what can we do about it? Well as I said, a field element is a pretty big number, so let's just encode our board into one:
class TicTacToe extends SmartContract {
// The board is serialized as a single field element
@state(Field) board: State<Field>;
}
We'll also need to keep track of who's turn is it, and if the game is finished (someone has won):
class TicTacToe extends SmartContract {
// The board is serialized as a single field element
@state(Field) board: State<Field>;
// false -> player 1 | true -> player 2
@state(Bool) nextPlayer: State<Bool>;
// defaults to false, set to true when a player wins
@state(Bool) gameDone: State<Bool>;
// player 1's public key
player1: PublicKey;
// player 2's public key
player2: PublicKey;
}
Notice that the public keys of the players are not decorated with @state. This is because we don't need to store that information on chain, we can simply hardcode it in the zkapp. If you wanted to be able to start a new game with new players, you would store these on chain so that you could mutate them via a method of the zkapp. But we're keeping it simple.
Also, PublicKey and Bool are two types provided by the standard library and built on top of Field. Bool is built on top of a single field element, so in total our on-chain state has 3 field elements. That'll work!
A constructor
Next, we must initialize that state in a constructor. let's look at the code:
class TicTacToe extends SmartContract {
// The board is serialized as a single field element
@state(Field) board: State<Field>;
// false -> player 1 | true -> player 2
@state(Bool) nextPlayer: State<Bool>;
// defaults to false, set to true when a player wins
@state(Bool) gameDone: State<Bool>;
// player 1's public key
player1: PublicKey;
// player 2's public key
player2: PublicKey;
// initialization
constructor(
initialBalance: UInt64,
address: PublicKey,
player1: PublicKey,
player2: PublicKey
) {
super(address);
this.balance.addInPlace(initialBalance);
this.board = State.init(Field.zero);
this.nextPlayer = State.init(new Bool(false)); // player 1 starts
this.gameDone = State.init(new Bool(false));
// set the public key of the players
this.player1 = player1;
this.player2 = player2;
}
}
The constructor does two things that might look weird. First, it takes an address as argument, this is the address where the zkapp will be deployed (this might disappear in future versions of snarky). Second, the constructor takes an initialBalance, which might be needed to pay the account creation fee (if you haven't already). The rest should be pretty straight forward.
Adding methods to the zkapp
We really only need one method: a method to play. We can create one with the @method decorator:
class TicTacToe extends SmartContract {
// ...
@method async play(
pubkey: PublicKey,
signature: Signature,
x: Field,
y: Field
) {
// ...
}
}
The method takes the player's public key, two coordinates, and a signature (to make sure that they own the public key) over the coordinates.
The board can be visualized as such:

The logic, at a high-level
Let's look at the logic that we will have to implement:
class TicTacToe extends SmartContract {
// ...
@method async play(
pubkey: PublicKey,
signature: Signature,
x: Field,
y: Field
) {
// 1. if the game is already finished, abort.
// 2. ensure that we know the private key associated to the public key
// and that our public key is known to the zkapp
// 3. Make sure that it's our turn,
// and set the state for the next player
// 4. get and deserialize the board
// 5. update the board (and the state) with our move
// 6. did I just win? If so, update the state as well
}
Does that make sense? In the rest of this tutorial I go over every step
Step 1: Game over is game over
if the game is already finished, abort.
To do this, we have to read the state of the zkapp with get. When you execute the program locally, this will go and fetch the state of the zkapp from the blockchain (hence the asynchronous call with await). Your execution will then only be deemed valid by the network if they see the same state (in this case the value of gameDone) on their side.
const finished = await this.gameDone.get();
finished.assertEquals(false);
Using assert functions like [assertEquals()] is the natural way to abort the program if it takes the wrong path. Under the hood, what happens is that the prover won't be able to satisfy the circuit and create a proof if the assert is triggered.
Step 2: Access control
ensure that we know the private key associated to the public key and that our public key is known to the zkapp
First, let's verify that the public key is one of the hardcoded key:
Bool
.or(pubkey.equals(this.player1), pubkey.equals(this.player2))
.assertEquals(true);
Next, let's verify that the player truly owns the private key associated with that public key by verifying a signature over the coordinates.
signature.verify(pubkey, [x, y]).assertEquals(true);
Step 3: taking turns
Make sure that it's our turn, and set the state for the next player
Earlier, we encoded a player as a boolean, with false describing the first player and true the second one. So let's derive this first.
In zero-knowledge proofs, we can't have branches with too much logic. The program pretty much always has to do the same thing. That being said, what we can do is to assign a different value to a variable depending on a condition. For example, this is how we can get the boolean that describes us as a player:
// get player token
const player = Circuit.if(
pubkey.equals(this.player1),
new Bool(false),
new Bool(true)
);
Circuit.if() takes three arguments, the first one is a condition that must be a Bool type, the other two are the returned values depending on if the condition is true or false.
Now that we have the player value, we can use it to check if it our turn:
// ensure its their turn
const nextPlayer = await this.nextPlayer.get();
nextPlayer.assertEquals(player);
And we can update the state for the next player via the set() function:
// set the next player
this.nextPlayer.set(player.not());
Step 4: fitting a board in a field element
get and deserialize the board
There's many strategies here, but a simple one is to deserialize the field element into bits (via toBits()) and interpret these bits as the board.
const serialized_board = await this.board.get();
const bits = serialized_board.toBits(9);
We can simply flatten the board like this:

Yet, this is not enough. A bit can only represent two states, and we have three: empty, false (player 1), true (player 2).
So we'll use two lists of size 9 instead:
- one to track who played on that tile
- and one to track if a tile is empty or not

As you can see, it is important to track if a tile is empty or not, because in the first list 0 represents both the empty tile and a move from the player 1.
const serialized_board = await this.board.get();
const bits = serialized_board.toBits(9 * 2);
const bits_not_empty = bits.slice(0, 9);
const bits_player = bits.slice(9, 18);
let board = [];
for (let i = 0; i < 3; i++) {
let row = [];
for (let j = 0; j < 3; j++) {
const not_empty = bits_not_empty[i * 3 + j];
const player = bits_player[i * 3 + j];
row.push([not_empty, player]);
}
board.push(row);
}
To make the rest of the logic easier to read, I'm going to use the Optional type to encode the [not_empty, player] array. It looks like this:
class Optional<T> {
isSome: Bool;
value: T;
// ...
}
It is simply a Bool that describes if it's empty (no one has played that tile yet), and if it's not empty the value associated with it (a cross or a circle, encoded as the player Bool).
Here's what the full deserialization code looks like:
const serialized_board = await this.board.get();
const bits = serialized_board.toBits(9 * 2);
const bits_not_empty = bits.slice(0, 9);
const bits_player = bits.slice(9, 18);
let board = [];
for (let i = 0; i < 3; i++) {
let row = [];
for (let j = 0; j < 3; j++) {
const not_empty = bits_not_empty[i * 3 + j];
const player = bits_player[i * 3 + j];
row.push(new Optional(not_empty, player));
}
board.push(row);
}
Step 5: Updating the board
update the board (and the state) with our move
Before we do anything, we need to check that the coordinates are valid:
x.equals(Field.zero)
.or(x.equals(Field.one))
.or(x.equals(new Field(2)))
.assertEquals(true);
y.equals(Field.zero)
.or(y.equals(Field.one))
.or(y.equals(new Field(2)))
.assertEquals(true);
Now here comes the trickiest part. Zero-knowledge smart contracts have some constraints: they don't allow you to dynamically index into an array, so you can't do this:
board[x][y].isSome = new Bool(true);
board[x][y].value = player;
instead, you have to go through every tile, and check if it's the one to update. (Note that you can't have dynamic for loops as well, they need to be of constant size).
for (let i = 0; i < 3; i++) {
for (let j = 0; j < 3; j++) {
// is this the cell the player wants to play?
const to_update = Circuit.if(
x.equals(new Field(i)).and(y.equals(new Field(j))),
new Bool(true),
new Bool(false)
);
}
}
And you can use the same tricks to make sure you can play on the tile, and to update the board:
for (let i = 0; i < 3; i++) {
for (let j = 0; j < 3; j++) {
// is this the cell the player wants to play?
const to_update = Circuit.if(
x.equals(new Field(i)).and(y.equals(new Field(j))),
new Bool(true),
new Bool(false)
);
// make sure we can play there
Circuit.if(
to_update,
board[i][j].isSome,
new Bool(false)
).assertEquals(false);
// copy the board (or update)
board[i][j] = Circuit.if(
to_update,
new Optional(new Bool(true), player),
board[i][j]
);
}
}
Finally, we can serialize and store this update into the zkapp's state:
// serialize
let not_empty = [];
let player = [];
for (let i = 0; i < 3; i++) {
for (let j = 0; j < 3; j++) {
not_empty.push(this.board[i][j].isSome);
player.push(this.board[i][j].value);
}
}
const new_board = Field.ofBits(not_empty.concat(player));
// update state
this.board.set(new_board);
Step 6: Did I just win?
did I just win? If so, update the state as well
Finally, we can check if someone won by checking all rows, columns, and diagonals. This part is a bit tedious and boring, so here's the code:
let won = new Bool(false);
// check rows
for (let i = 0; i < 3; i++) {
let row = this.board[i][0].isSome;
row = row.and(this.board[i][1].isSome);
row = row.and(this.board[i][2].isSome);
row = row.and(this.board[i][0].value.equals(this.board[i][1].value));
row = row.and(this.board[i][1].value.equals(this.board[i][2].value));
won = won.or(row);
}
// check cols
for (let i = 0; i < 3; i++) {
let col = this.board[0][i].isSome;
col = col.and(this.board[1][i].isSome);
col = col.and(this.board[2][i].isSome);
col = col.and(this.board[0][i].value.equals(this.board[1][i].value));
col = col.and(this.board[1][i].value.equals(this.board[2][i].value));
won = won.or(col);
}
// check diagonals
let diag1 = this.board[0][0].isSome;
diag1 = diag1.and(this.board[1][1].isSome);
diag1 = diag1.and(this.board[2][2].isSome);
diag1 = diag1.and(this.board[0][0].value.equals(this.board[1][1].value));
diag1 = diag1.and(this.board[1][1].value.equals(this.board[2][2].value));
won = won.or(diag1);
let diag2 = this.board[0][2].isSome;
diag2 = diag2.and(this.board[1][1].isSome);
diag2 = diag2.and(this.board[0][2].isSome);
diag2 = diag2.and(this.board[0][2].value.equals(this.board[1][1].value));
diag2 = diag2.and(this.board[1][1].value.equals(this.board[2][0].value));
won = won.or(diag2);
// update the state
this.gameDone.set(won);
The full code is available here if you want to play with it.
Moxie just wrote his first impressions on web3. If you've been wondering about web3, and want a non-bullshit and technical glance at what it is, I think this is a really good post.
While I do agree with his critics, I don't share his skepticism. Let's look at his description of how most users interact with decentralized apps (dapps):
For example, whether it’s running on mobile or the web, a dApp like Autonomous Art or First Derivative needs to interact with the blockchain somehow – in order to modify or render state (the collectively produced work of art, the edit history for it, the NFT derivatives, etc). That’s not really possible to do from the client, though, since the blockchain can’t live on your mobile device (or in your desktop browser realistically). So the only alternative is to interact with the blockchain via a node that’s running remotely on a server somewhere.
A server! But, as we know, people don’t want to run their own servers. As it happens, companies have emerged that sell API access to an ethereum node they run as a service, along with providing analytics, enhanced APIs they’ve built on top of the default ethereum APIs, and access to historical transactions. Which sounds… familiar. At this point, there are basically two companies. Almost all dApps use either Infura or Alchemy in order to interact with the blockchain. In fact, even when you connect a wallet like MetaMask to a dApp, and the dApp interacts with the blockchain via your wallet, MetaMask is just making calls to Infura!
This is a real problem. To interact with the blockchain, you need to download its whole history with a program. This takes a lot of time (sometimes days) and space. This is not realistic for most users, and even less so for mobile users. The solution has been to just trust a public node. Infura is one of them and has become quite "trusted" through being the backend behind Metamask, the most popular Ethereum wallet. This service can lie to you, and you wouldn't notice. As such, the whole security of the blockchain is moot once you start interacting through a public node.
“It’s early days still” is the most common refrain I see from people in the web3 space when discussing matters like these. In some ways, cryptocurrency’s failure to scale beyond relatively nascent engineering is what makes it possible to consider the days “early,” since objectively it has already been a decade or more.
Did you know that most of the web was not encrypted until recently? For example, Facebook defaulted to https in 2013. Not even a decade ago. Cryptocurrencies have come a long way since the advent of Bitcoin, and research has exploded in all directions. It is early days.
Now, what are the actual solutions that exist in the space?
First, newer byzantine-fault tolerant (BFT) consensus protocols have straight-forward solutions to this problem. Since each block is cryptographically certified by consensus participants, and no re-organization (or forks) can happen, the certification can be reused to provide a proof to the clients (the real ones). As such, Infura could very well give you this cryptographic proof to accompany a response to your request, and the problem would be fixed. This is what Celo is doing with Plumo, but more generally any blockchain that uses a BFT consensus (Diem/Libra, Cosmos, Algorand, Dfinity, etc.) should be able to implement something like this.
The security guarantee is not as high as verifying every block since the beginning of time (the genesis). (For this, cryptocurrencies like Mina have proposed recursive zero-knowledge proofs solutions that attest to all the state transition since genesis.) Plumo calls this ultra-light clients:
We observe that in order to verify the latest block header in BFT networks a client only needs the public keys of the current committee. As long as no committee has had a dishonest supermajority, a client who verifies a chain of committee hand-off messages certifying the PoS election results, known as epoch messages, does not need to check each block or even the headers of each block. Instead, to make (or verify a recent) transaction, the client simply asks for the latest (or otherwise relevant) block header, and verifies that it has been signed by a supermajority of the current committee. This constitutes the simplifying assumption (SA) and light client protocol proved by Plumo.
Another issue is key rotations, which increase the size of the proof (as you need to give proofs to all the key rotations before you can give a proof to the latest state of the chain), but I believe that zero-knowledge proofs can fix that as well.
Bottom line: it's actually not that grim, solutions are there, but users have to care for people to implement them, apply them, and for the solutions to receive adoption. OK, this is pretty much what Moxie says:
However, even if this is just the beginning (and it very well might be!), I’m not sure we should consider that any consolation. I think the opposite might be true; it seems like we should take notice that from the very beginning, these technologies immediately tended towards centralization through platforms in order for them to be realized, that this has ~zero negatively felt effect on the velocity of the ecosystem, and that most participants don’t even know or care it’s happening. This might suggest that decentralization itself is not actually of immediate practical or pressing importance to the majority of people downstream, that the only amount of decentralization people want is the minimum amount required for something to exist, and that if not very consciously accounted for, these forces will push us further from rather than closer to the ideal outcome as the days become less early.
But this is not counting on Infura getting hacked. And it will get hacked.
I spent some days over Christmas to read the paper Cairo – a Turing-complete STARK-friendly CPU architecture. First, it's a work of art. I find a lot of the papers in the field of general-purpose zero-knowledge proofs (GP-ZKPs) quite hard to read, but this one has a lot of emphasis on the flow and on examples. More than that, the ideas contained in the paper are quite mind-blowing (although everything is mind-blowing in the land of GP-ZKPs).
What is this paper? It's the layout, in quite the detail, of a protocol that can be used to produce zero-knowledge proofs that a program executed correctly (what they call proof of computational integrity*). While most approaches "compile" each program into its fixed protocol (with a prover part and a verifier part), Cairo is a single protocol that works for any program (of some bounded size of course). They call this the CPU approach, as opposed to the ASIC approach. Effectively, the program you want to prove is encoded in some Cairo instruction set and passed as input to another program that will simply run it, like a VM. Translated in ZKP-lingo, a circuit will constrain the execution trace to match the execution of the program passed as public input. (This last sentence might be hard to understand if you are not familiar with at least one GP-ZKP system.)
Cairo is also a higher-level language, that you can play with on the Cairo playground. If you click on "debug" you can see the program it compiles to. Essentially a series of instructions and data, which you can think of as code and data segments of a binary. The rest of the memory essentially acts as a "stack" that is used during the execution of the program.
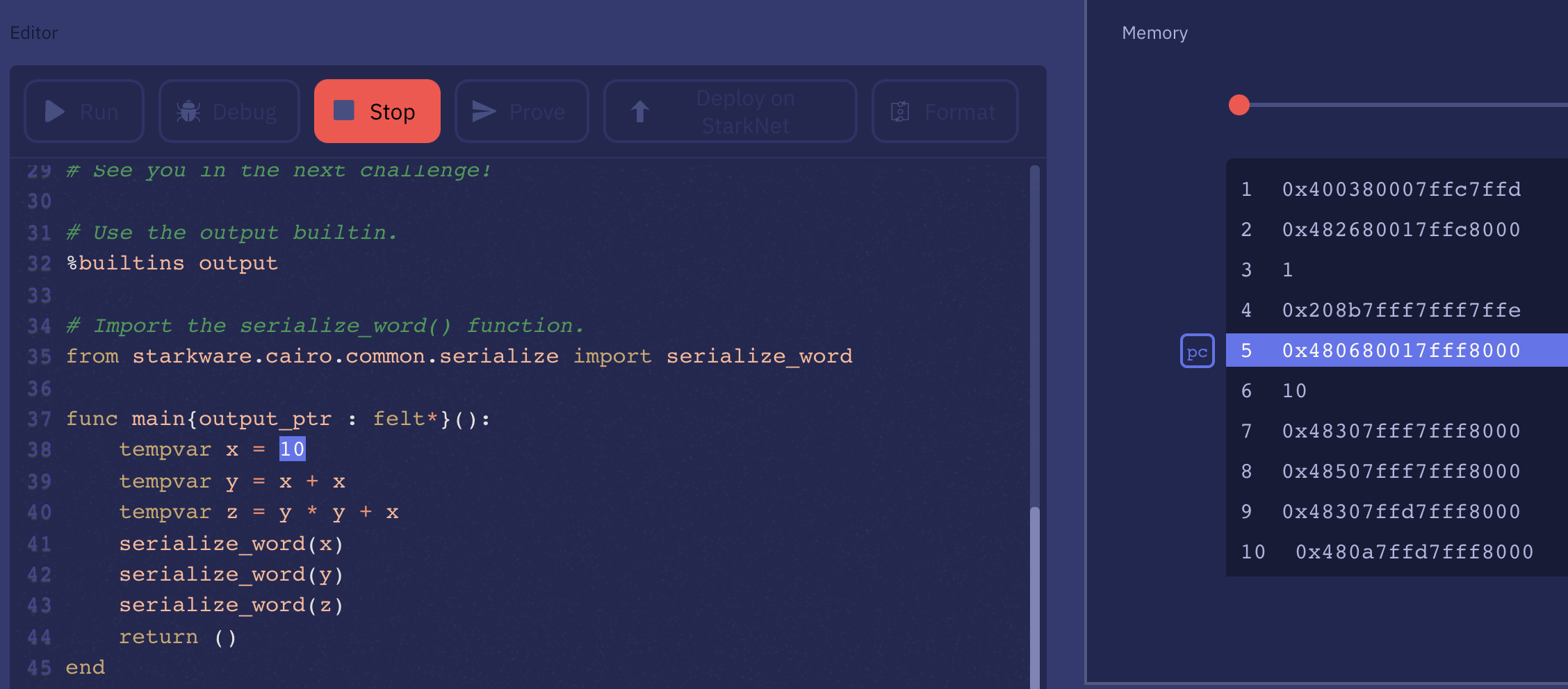
The higher-level language is out of scope of the paper. Instead, the paper details the set of instructions and its encoding, which is then unpacked in the constraint of the circuit executing the program. In the paper, they go through a simple example, the Fibonacci sequence, to illustrate how a program works and how the state transition logic works. As I had to reverse engineer it I thought I would share this here.

Here's our program, which is two instructions followed by three values.
Let's start simple and let's look at what the first instruction tells us.
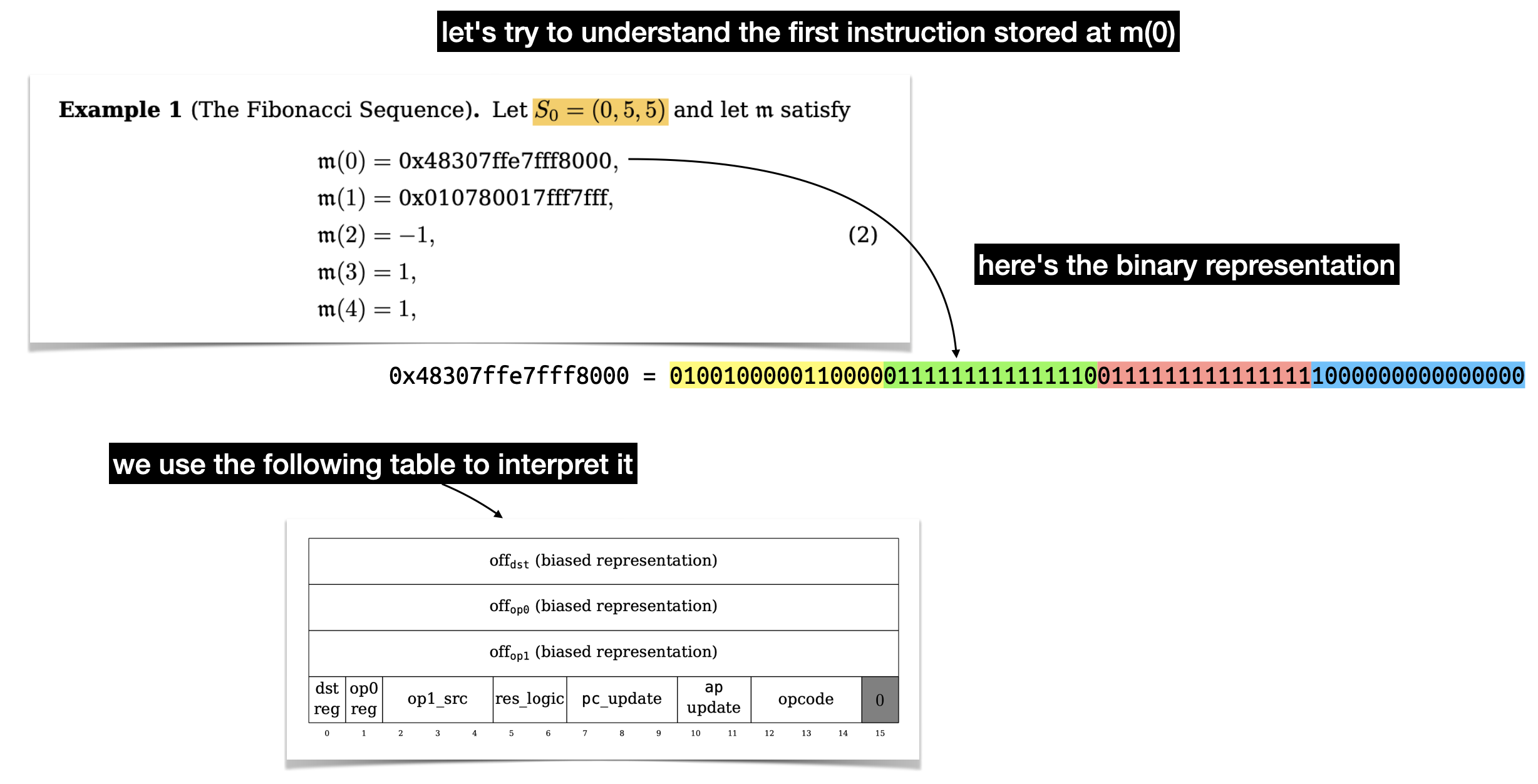
There's a lot to unpack here, there's three values of 16 bits that represent offsets in our memory. Two for the two operands (op0 and op1) of a binary operation, and one (dst) to indicate where to store the result of the operation. Let's ignore these for now and focus on the last part: the flags.
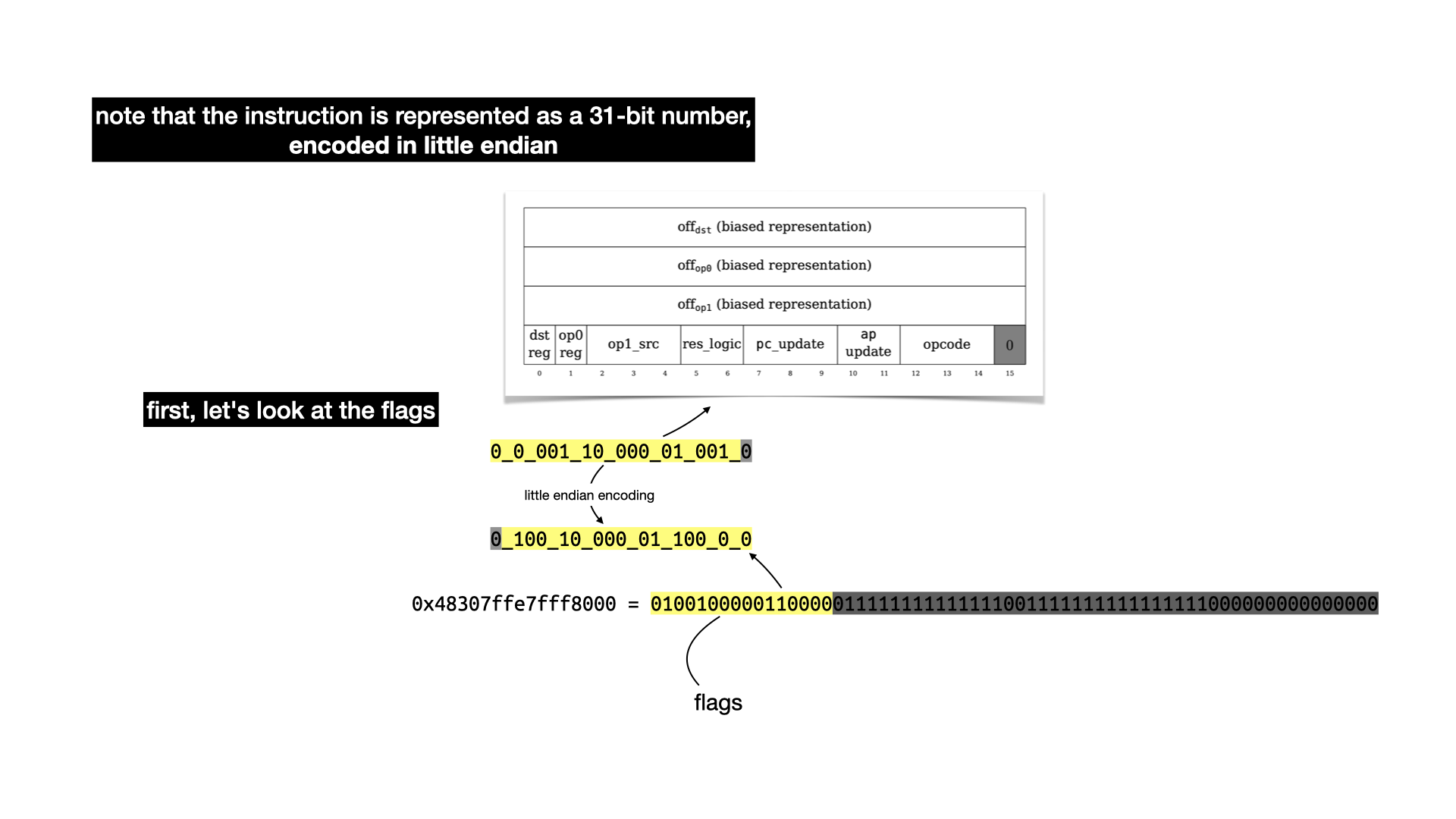
To understand what each flags do, you have to take a look at the state transition function. It's a bit confusing to follow, but there's apparently a Lean proof that it is correct (this field really keeps on giving).

A lot of this is not going to make sense without reading the paper. But there's three registers:
pc is the program counter, it points to an address in memory from where to fetch the next instruction.ap is the allocation pointer, it points to a free address in memory, useful to store data globally.fp is the frame pointer, used to store data as well when doing function calls.
The logic can be summarized as: fetch data from memory; operate on it (addition or multiplication); update the registers.
So what happens with our example's first instruction?
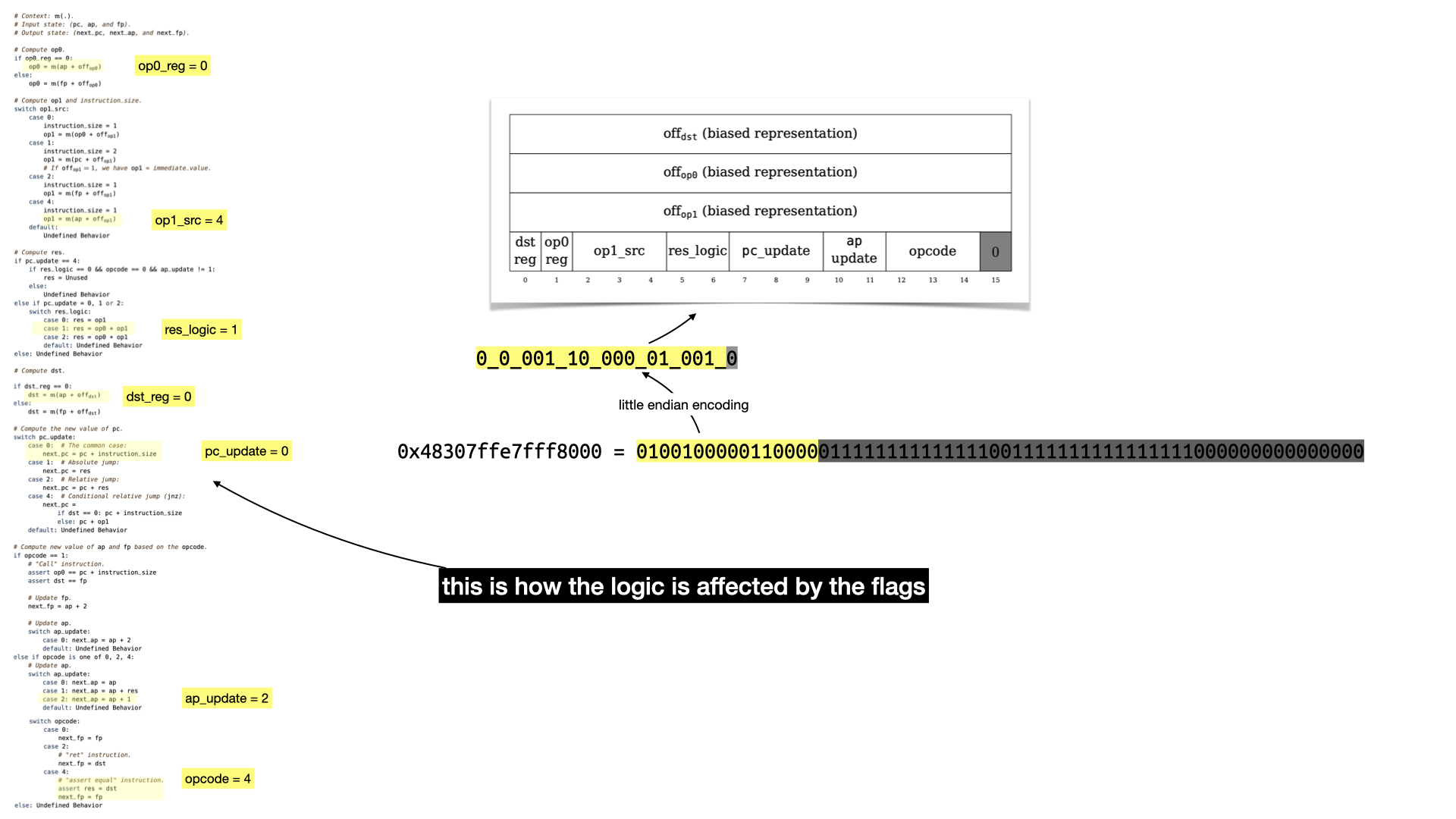
Still a bit abstract but that should give you an idea.
Before I reveal the result of the whole instruction let's look at the rest of the instruction: the offsets

The offset leaks some of the logic: -1 and -2 are the indices in the Fibonacci formula
$u_i = u_{i-1} + u_{u-2}$
Let's now reveal what the first instruction is really doing.
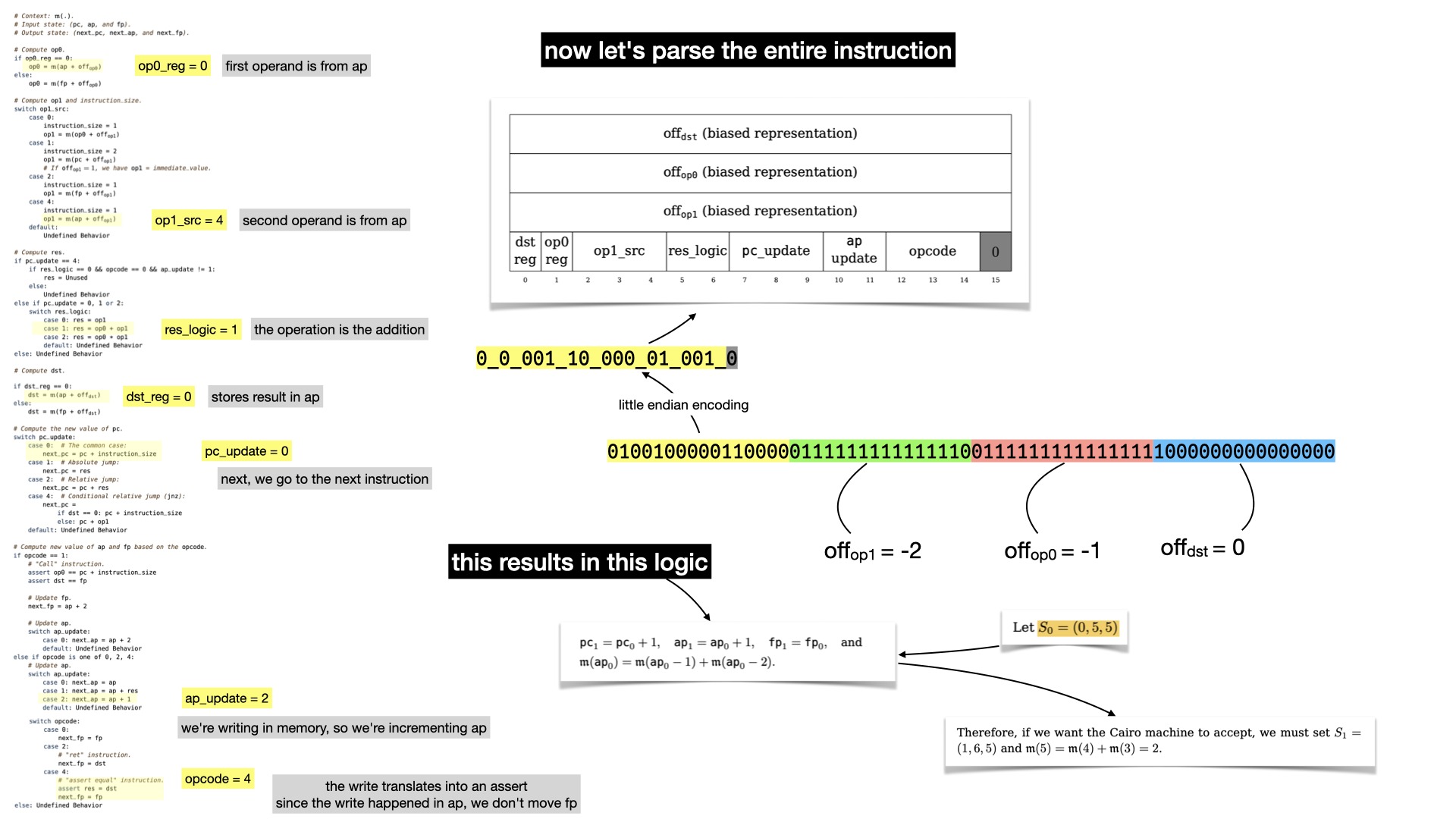
There's no doubt that if you've followed that far you must have read the paper.
What happens can be summarized as:
- we increment the program counter
pc (to go to the next instruction)
- we add the two values stored in the memory at offset
-1 and -2, and store the result in memory.
- we increment
ap, since we stored in memory. We don't touch fp since we didn't do any function call.
Let's look at the second instruction.

Let's reverse it using our table.
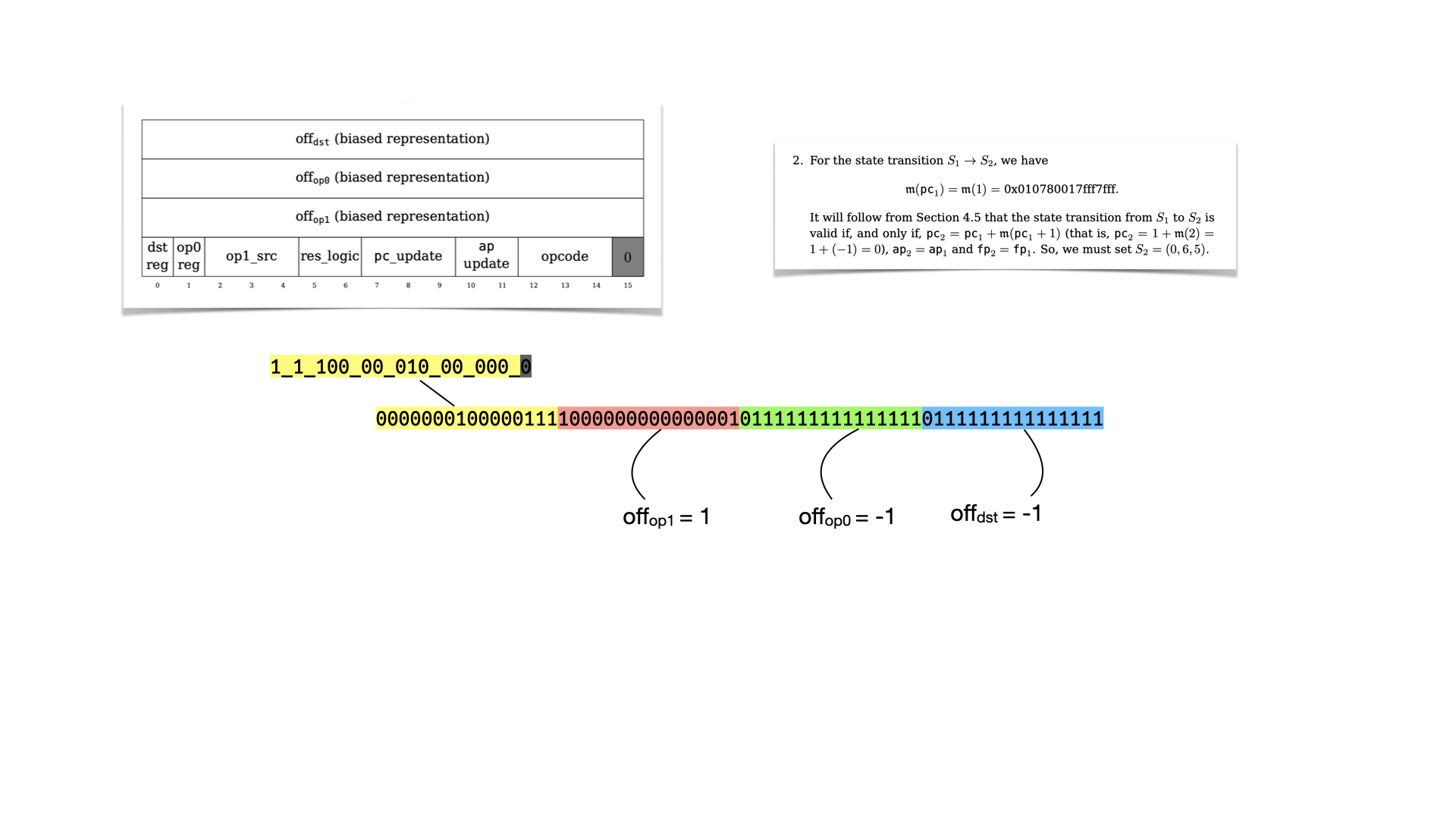
And let's look at the flags
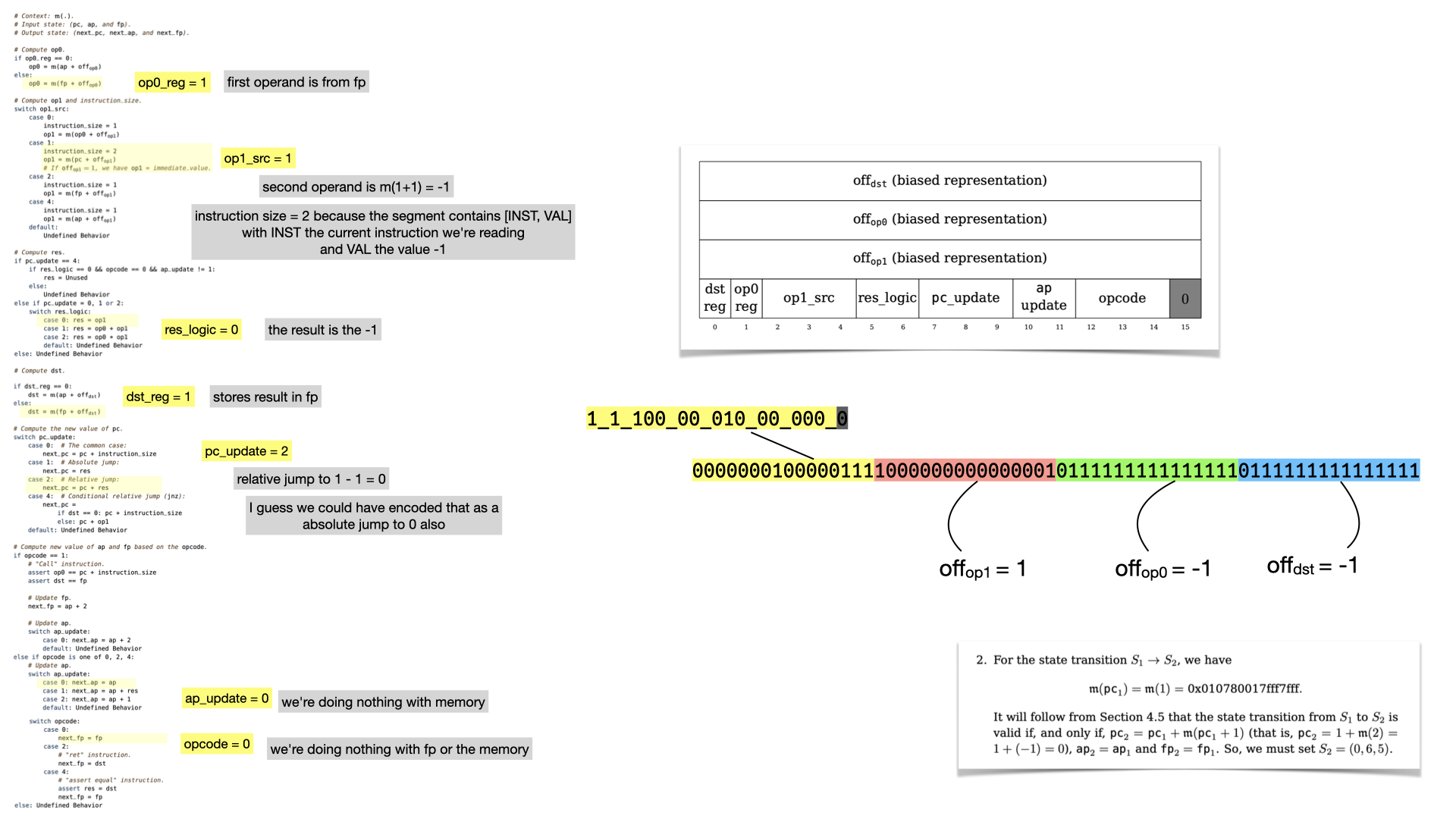
What's interesting here, is that the instruction leads to a jump! The next register values will lead to the circuit re-starting from instruction at memory address 0, because pc points to it. Thus, we're in an infinite loop, which is parameterized by the number of instructions that the prover wants to run.

I got interviewed by Quartz for their Listen to the crypto converts article.
Wong is a cryptography engineer at software development company O(1) Labs, working on the Mina cryptocurrency. He writes about crypto and cryptography at his blog, cryptologie.net, and was previously the security lead for Facebook’s Diem.
read the full interview here
I've been reading a lot of negative discussions around cryptocurrencies on some of the communities that I frequent (e.g. hackernews) and I felt the urge to write something about it.
I personally find cryptocurrencies to be an extremely interesting field of innovation because it tightly involves three interesting domains:
- The field of cryptography
- The field of economics
- The current payment system and the financial world
Lacking knowledge in any of these fields makes it extremely hard to have a good understanding of the added value of cryptocurrencies. Money is quite an abstract subject (what's a derivative? what's a CDO? what's a margin call? etc.) and it can take decades to understand how a new technology can impact money and society in general. In this post, I give my own opinion of what problems cryptocurrencies can address, while warning readers that I'm mostly involved in the field of cryptography, know a bit about the financial world, and know very little about economics. So take this post with the usual grain of salt.
The point where Blockchain became mainstream
Years ago, I was waiting in line on a beach in Chicago. I had been standing there for hours to try the HTC Vive, a virtual reality headset. What was waiting for me at the end of the line was the future, I believed it before I tried it, and I understood it after experiencing it. Yet, I managed to miss another hint of the coming times, a change that was unraveling in plain sight, invisible to my oblivious eyes.
In line, I started chatting with some older chap who got really enthusiastic when I mentioned that I was working in cryptography.
"So what do you think about the blockchain?"
I had known Bitcoin for a while at that time, but this was the first someone that appeared non-technical talked about a cryptographic term directly.
"You mean Bitcoin?"
"Yeah"
"Ah, well, I'm not sure, what else is there than the cryptocurrency itself?"
The dude then started asking me questions about where I thought the "technology" would go and how revolutionary I thought it was. Odd, I remember thinking. I couldn't see why that person was so hyped and I dismissed it as misdirected enthusiasm, thinking that there was really nothing more to Bitcoin than Bitcoin.
It's comical, in retrospect, that I failed hard to foresee the boom of the cryptocurrencies. I had invested some, and lost some during the first mtgox crash), I had even made a presentation to my classmates a few years ago as I was doing a masters on cryptography. I had found the idea really cool, perhaps it was one of the reason I ended up studying cryptography? But still, why would anyone see something more than the initial Bitcoin paper?
For many years I continued to ignore cryptocurrencies. I didn't get why more and more people would get excited. I even created some passive aggressive page, annoyed by the new use of the term "crypto" (http://cryptoisnotcryptocurrency.com).
In 2017, everything changed. At the time, I was working as a security consultant at the Cryptography Services department of NCC Group, and suddenly my team started getting more and more cryptocurrency-related work. And in turn, I got more and more interested and involved in the world of cryptocurrencies, creating the Decentralized Application Security Project Top 10 and participating in the audits of cryptocurrencies like NuCypher, Ethereum, and ZCash. The next thing I know I was leading security for the Diem cryptocurrency (formerly known as Libra) working at Novi (Facebook), two years later I was joining the cryptography team of O(1) Labs to work on the Mina cryptocurrency, and a few month ago publishing Real-World Cryptography, the first cryptography book with a chapter on cryptocurrencies.
The state of banking today
Cryptocurrencies are about the movement of money, and as such it is important to study the current ways and limitations of moving money. Without this context, cryptocurrencies do not make any sense.
Today, payment works something like this: for your bank to reach someone else's bank (your friend, your landlord, or a souvenir shop in Thailand) it needs to travel through several banks and systems. In practice, not all banks have partnerships with one another, and so your bank will have to find a route to take to reach the other bank. Different destinations mean different routes.
Banks allow movement of money by creating partnerships with other banks. It usually works like this: bank A has an account at bank B, and bank B has an account at bank A. We call that correspondent banking. If bank A wants to send some money to bank B, they'll either credit bank B's account, or bank B will debit bank A's account. (The direction might be decided on how much bank A trusts B, and vice versa.)
Of course, not all banks have partnerships, but following the six degrees of separation concept, there'll usually be a chain of banks that connect your bank from your recipient's bank.
If you're sending money within the same country, and depending on the country you're living in, you might have access to a government-operated bank that will attempt to partner with most of the territory's banks. A so-called central bank. In the US it's the Federal Reserve System (or the Fed), in France it's Banque de France, etc. Central banks have central banks too, for example, the Bank for International Settlements (BIS).
Now, let's talk speed: some of these central banks sometimes have real-time settlement systems, where money can be transferred from one bank to the other almost instantaneously. These are usually called real-time gross settlements (RTGSs), where "gross" means that you're not batching several transactions together. Most banks, as I understand, use deferred net settlements to batch transactions: once (or sometimes several times) a day money moves from one bank to another bank.
Thus, to transfer money from your bank to a recipient's bank, your money has to go through a chain of bank accounts. Some of these movements will be settled instantly, some of these movements will be settled after hours or days. This is why payments can be slow depending on the route your money takes.
Money is (badly) decentralized
If you dig deeper, you realize that different banks use different protocols, these protocols are old, badly designed, and errors happen constantly. The only way to make sure that money is not created out of thin air (double spending) is to constantly perform manual audits: having actual humans read balance sheets.
One of my friend working at a European bank described to me one of the many incidents they had. To settle with some other bank, they use some XML protocol to communicate how much Euro should move between the banks, and that twice a day. Usually, there's always money moving. Yet, one day, the correspondent bank did not send them any second transfer before the end of the day. My friend's bank took this as a "let's replay the previous settlement" and started crediting thousands of clients with sums of money they had already received. Employees had to work nights to revert everything and make sure that money was not lost. Imagine that.
And that's just one bank, every bank is doing their own thing to an extent. There are some standardization effort, as there usually is when things get bad, but they move slowly. It also doesn't fix the elephant in the room: money is too heavily and badly decentralized, and every bank is on a quest to partner with every other bank, creating an $O(n^2)$ nightmare.
All the solutions that attempt at fixing the system are pretty much trying to centralize more of the system. The fastest points of payments are central banks and other single points of failure like Wise. One interesting development is that some of these central banks are realizing that they need to support instant payments, better security, good interoperability, and perhaps all of that even for people like you and I (the retail). This is what you might have heard as central bank digital currencies (CBDCs).
This reduces the $O(n^2)$ issue, but it also introduces another one: the issue of trust. Why would central banks trust one another? The more you centralize, the more trust you need to have in that single point of failure.
This is the big innovation behind cryptocurrencies: they seek to centralize the financial backbone to facilitate the movement of money. That is, cryptocurrencies are distributed systems, which ultimate goal is to simulate centralized systems while removing single points of failure. In such systems, users all connect to what appears to be, and work like, a single server. No need to connect users between them, in the peer-to-peer way I described previously, now the simulated single machine is connecting everyone together. Money takes the shortest route possible.
In some sense, a cryptocurrency is like a central bank that anyone can connect to and that processes transfer in real time, but internally it has no single points of failure, provides insurance based on cryptography, and offers transparency to external users.
A tiny introduction to the fundamentals
Don't run away. I promise this is a tiny, brief, understandable, introduction to the fundamentals of cryptocurrencies.
Imagine that a hundred participants decide to create this centralized bank. To do that, they all decide to start from the same ledger, a book of all account balances (and transactions). The first page (or block) might read:
Bob has 3 tokens, Alice has 2 tokens
This is the genesis, in crypto term. Once each participant has retrieved their copy of the ledger, they need to figure out a way to agree on who gets to add new pages in the book. For example, adding a page could look like:
Alice sends 2 tokens to Charles; Bob sends 1 token to Alice
And as they add pages, they also need to make absolutely sure that they are all adding the same pages. If a participant adds a different page than everyone else, we have what we call a fork. That participant would start living in a different world.
A very simple way to decide on who gets to add pages to the ledger, is to do a round robin: I go first, then you, then him, then her, then me again, then you, etc. That works well if the set of participants is known and fixed (which is what Libra/Diem does, and it's called proof of authority).
Other cryptocurrencies might want to dynamically choose who gets to be the next leader based on how much tokens they have (this is called proof of stake, like Tendermint).
Now, Bitcoin did things differently, it let everybody have a chance at choosing the next page! To participate, you play a lottery with your computer and if you get the winning ticket you get to decide on the next set of transactions (the next block). This was called proof of work, and as you probably know it, the lottery is computationally expensive to play. Due to that, today, most modern cryptocurrencies use a proof of stake approach.
Last Tuesday was the start of ZK HACK, a "7-week virtual event featuring weekly workshops and advanced puzzle solving competitions". All related to zero-knowledge proofs, as the name suggests. The talks of the first day were really good, and you can rewatch them here. At the end of the first day, a puzzle called Let's hash it out was released. This post about solving this puzzle.
The puzzle
The puzzle is a Github repo containing a Rust program. If you run it, it displays the following message:
Alice designed an authentication system in which users gain access by presenting it a signature on a username, which Alice provided.
One day, Alice discovered 256 of these signatures were leaked publicly, but the secret key wasn't. Phew.
The next day, she found out someone accessed her system with a username she doesn't know! This shouldn't be possible due to existential unforgeability, as she never signed such a message.
Can you find out how it happend and produce a signature on your username?
Looking at the code, it looks like there's indeed 256 signatures over 256 messages (that are just hexadecimal strings though, not usernames).
The signature verification
The signatures are BLS signatures (a signature scheme that makes use of pairing and that I've talked about it here).
Looking at the code, there's nothing fancy in there. There's a verification function:
pub fn verify(pk: G2Affine, msg: &[u8], sig: G1Affine) {
let (_, h) = hash_to_curve(msg);
assert!(Bls12_381::product_of_pairings(&[
(
sig.into(),
G2Affine::prime_subgroup_generator().neg().into()
),
(h.into(), pk.into()),
])
.is_one());
}
which pretty much implements the BLS signature verification algorithm to check that
$$
e(\text{sig}, -G_2) \cdot e(\text{h}, \text{pk}) = 1
$$
Note: if you read one of the linked resource, "BLS for the rest of us", this should make sense. If anything is confusing in this section, spend a bit of time reading that article.
We know that the signature is simply the secret key $sk$ multiplied with the message:
$$\text{sig} = [\text{sk}]h$$
The public key is simply the secret key $\text{sk}$ hidden in the second group:
$$\text{pk} = [\text{sk}]G_2$$
So the check gives us:
$$
\begin{align}
& \;e([sk]h, -G_2) \cdot e(h, [sk]G2) \
=& \;e(h, G_2)^{-\text{sk}} \cdot e(h, G_2)^\text{sk} \
=& \;1
\end{align}
$$
The hash to curve
Actually, the username is not signed directly. Since a signature is the first argument in the pairing it needs to be an element of the first group (so $[k]G_1$ for some value $k$).
To transform some bytes into a field element $k$, we use what's called a hash-to-curve algorithm. Here's what the code implements:
pub fn hash_to_curve(msg: &[u8]) -> (Vec<u8>, G1Affine) {
let rng_pedersen = &mut ChaCha20Rng::from_seed([
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1,
]);
let parameters = CRH::<G1Projective, ZkHackPedersenWindow>::setup(rng_pedersen).unwrap();
let b2hash = blake2s_simd::blake2s(msg);
(
b2hash.as_bytes().to_vec(),
CRH::<G1Projective, ZkHackPedersenWindow>::evaluate(¶meters, b2hash.as_bytes())
.unwrap(),
)
}
What I'm reading is that it:
- initializes some collision-resistant hash function (CRH) from a hardcoded seed
- uses the BLAKE2 hash function to hash the username (
msg) into 256 bits.
- Uses the CRH to hash the BLAKE2 digest into a group element
Looking at CRH, it's simply a Pedersen hashing (I've talked about that hash function here) that converts a series of bits $b_1, b_2, b_3, \cdots$ into
$$
[b_1]G_{1,1} + [b_2]G_{1, 2} + [b_3]G_{1, 3} + \cdots
$$
where the $G_{1,i}$ are curve points that belongs to the first group (generated by $G_1$) and derived randomly via the hardcoded seed (in a way that prevents anyone from guessing their discrete logarithm).
What are we doing?
What are we looking for? We're trying to create a valid signature (maybe a signature forgery attack then?) on our own nickname (so more than just an existantial forgery, a chosen-message attack).
We can't change the public key (so no rogue key attack), and the message is fixed. This leaves us with the signature as the only thing that can be changed. So indeed, a signature forgery attack.
To recap, we have 256 valid signatures:
- $e(\text{sig}_1, -G_2) \cdot e(h(m_1), \text{pk}) = 1$
- $\vdots$
- $e(\text{sig}_{256}, -G_2) \cdot e(h(m_{256}), \text{pk}) = 1$
and we want to forge a new one such that:
$$
e(\text{bad_sig}, -G_2) \cdot e(h(\text{"my nickname"}), \text{pk}) = 1
$$
Forging a signature
Reading on the aggregation capabilities of BLS, it seems like the whole point of that signature scheme is that we can just add things with one another. So let's try to think about adding signatures shall we?
What happens if I add two signatures?
$$
\begin{align}
&\; \text{sig}_1 + \text{sig}_2 \
=&\; [\text{sk}]h_1 + [\text{sk}]h_2
\end{align}
$$
if only we could factor $sk$ out... but wait, we know that $h_1$ and $h_2$ are additions of the same curve points (by definition of the Pedersen hashing):
$$
\begin{align}
&\; \text{sig}_1 + \text{sig}_2 \
=&\; [\text{sk}]h_1 + [\text{sk}]h_2 \
=&\; \text{sk}\
&\; + \text{sk}
\end{align}
$$
where the $b_{i}$ (resp. $b'_{i}$) are the bits of $h_1$ (resp. $h_2$). So the added signature are equal to the signature of the added bitstrings:
$$
[b_{1} + b'{1},\; b{2} + b'{2},\; b{3} + b'_{3},\; \cdots]
$$
We just forged a signature! Now, that shouldn't mean much, because remember, these bits represent the output of a hash function and a hash function is resistant against pre-image attacks.
Wait a minute...
Our hash function is a collision-resistant hash function, but that's it.
Linear combinations
OK, so we forged a signature by adding two signatures. But we probably didn't get what we wanted, what we wanted is to obtain the bits $\tilde{b}_1, \tilde{b}_2, \tilde{b}_3, \cdots$ that represent the hashing of my own username.
Maybe if we add more signatures together we can get? Actually, we can use all the signatures and combine them. And not just by adding them, we can take any linear combination (we're in a field, not constrained by 0 and 1).
So here's the system of equations that we have to solve:
- $\tilde{b}_1 = x_1 b_1 + x_2 b'_1 + x_3 b''_1$
- $\vdots$
- $\tilde{b}_{256} = x_1 b_{256} + x_2 b'_{256} + x_3 b''_{256}$
Note that we can see that as solving $xA = b$ where each row of the matrix $A$ represents the bits of a digest, and $b$ is the bitvector of my digest (the hash of my username).
Once we find that linear combinations, we just have to apply it to the signatures to obtain a signature that should work on my username :)
$$
\text{bad_sig} = x_1 \text{sig}_1 + x_2 \text{sig}_2 + x_3 \text{sig}_3 + \cdots
$$
Coding the answer
Because I couldn't find a way to solve a system of equations in Rust, I simply extracted what I needed and used Sage to do the complicated parts. Here's the Rust code that creates the matrix $A$ and the vector $b$:
// get puzzle data
let (_pk, ms, _sigs) = puzzle_data();
// here's my name pedersen hashed
let (digest_hash, _digest_point) = hash_to_curve("mimoo".as_bytes());
// what's that in terms of bits?
use ark_crypto_primitives::crh::pedersen::bytes_to_bits;
let bits = bytes_to_bits(&digest_hash);
let bits: Vec<u8> = bits.into_iter().map(|b| b as u8).collect();
// order of the subgroup of G1
println!("R = GF(0x73eda753299d7d483339d80809a1d80553bda402fffe5bfeffffffff00000001)");
// xA = b
print!("A = matrix(R, [");
for m in ms {
let (digest, _point) = hash_to_curve(&m);
let bits = bytes_to_bits(&digest);
let bits: Vec<u8> = bits.into_iter().map(|x| x as u8).collect();
print!("{:?}, ", bits);
}
println!("b = vector(R, {:?})", bits);
Note: the system of equation is over some field $R$. Why? Because eventually, the linear combination happens between curve points that are elements of the first group, generated by $G_1$, and as such are scalars that live in the field created by the order of the group generated by $G_1$.
In sage, I simply have to write the following:
x = A.solve_left(b)
and back in Rust we can use these coefficients to add the different signatures with one another:
let mut bad_sig = G1Projective::zero();
for (coeff, sig) in coeffs.into_iter().zip(sigs) {
let coeff = string_int_to_field_el(coeff);
bad_sig += sig.mul(coeff);
}
// the solution
verify(pk, "mimoo".as_bytes(), bad_sig.into());
It works!




















