Schnorr just released a new paper Fast Factoring Integers by SVP Algorithms with the words "This destroyes the RSA cryptosystem." (spelling included) in the abstract.
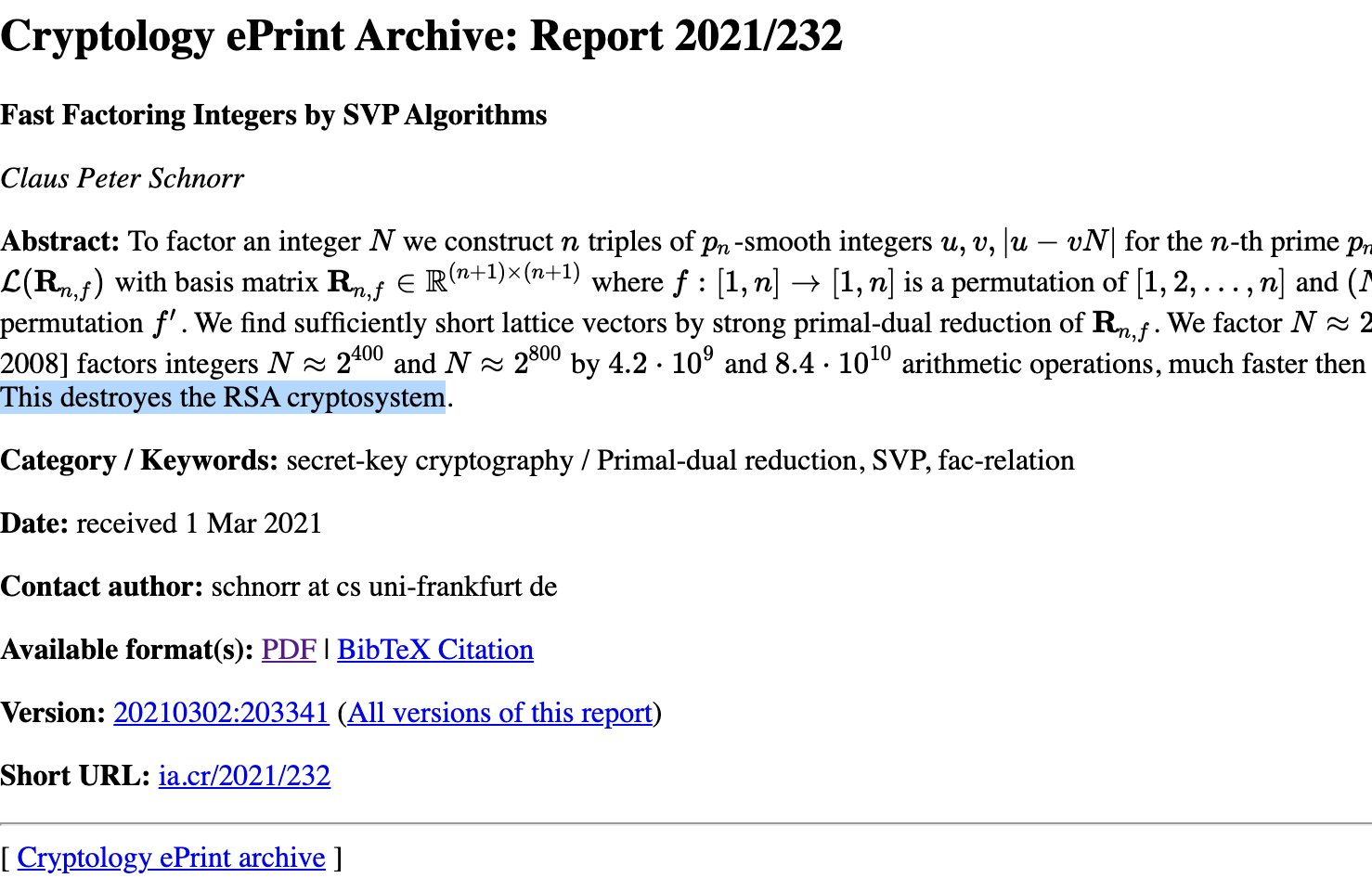
What does this really mean? The paper is honestly quite dense to read and there's no conclusion in there.
UPDATE: Several people have pointed out that the "This destroyes the RSA cryptosystem" is not present in the paper itself, that is until the paper was updated to include the sentence without the typo.
UPDATE: There was some discussion about a potential fake, but several people in the industry are confirming that this is from Schnorr himself:
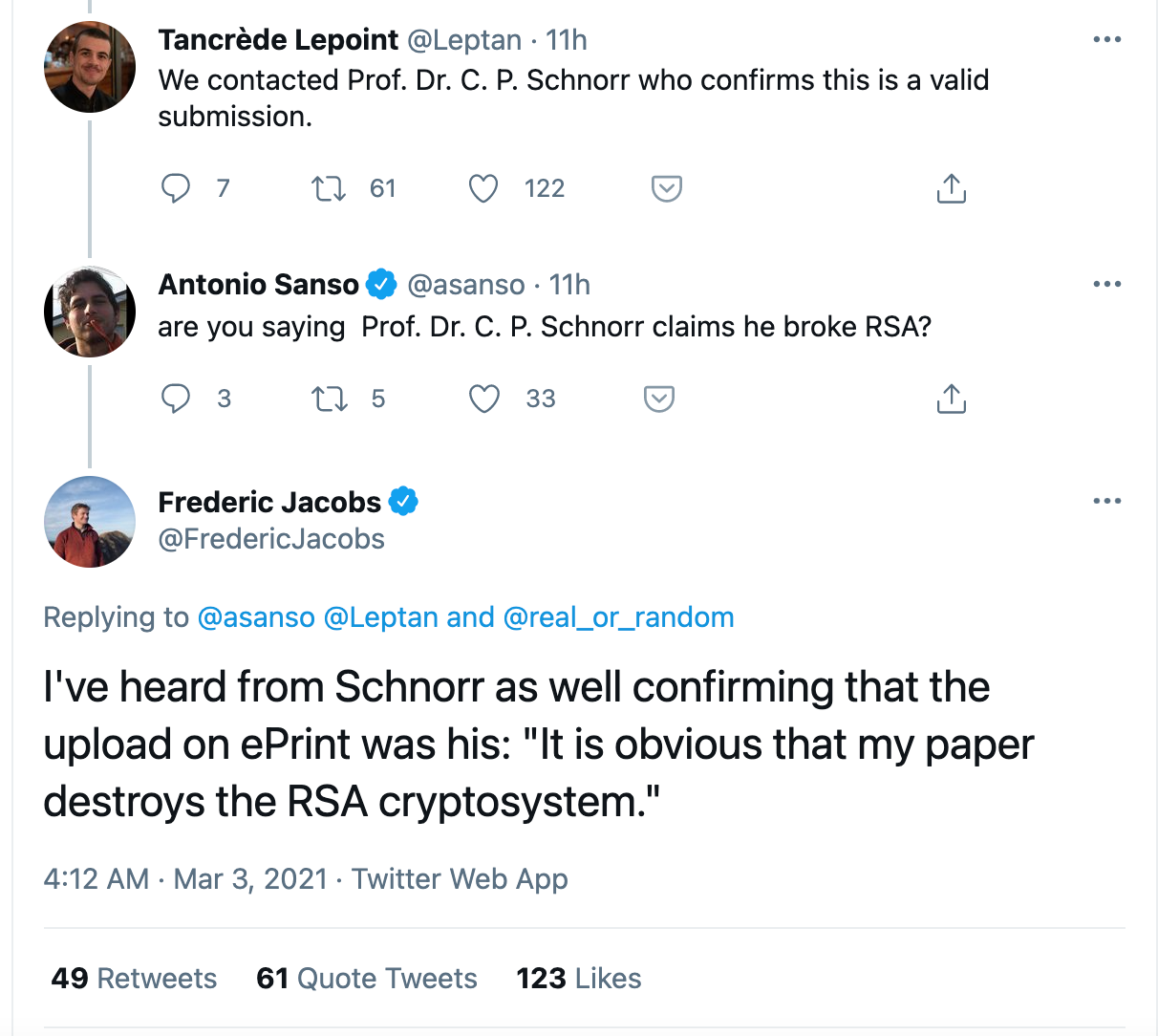
UPDATE: Sweis is calling for a proof of concept:
According to the claims in Schnorr’s paper, it should be practical to set significant new factoring records. There is a convenient 862-bit RSA challenge that has not been factored yet. Posting its factors, as done for the CADO-NFS team’s records, would lend credence to Schnorr’s paper and encourage more review of the methodology.
UPDATE: Léo Ducas has been trying to implement the claim, without success.
UPDATE: Geoffroy Couteau thinks the claim is wrong:
several top experts on SVP and CVP algorithms have looked at the paper and concluded that it is incorrect (I cannot provide names, since it was in the context of anonymous reviews).
UPDATE: Daniel Shiu pointed out an error in the paper
UPDATE: Pedro Fortuny Ayuso is very skeptical of the claim. Will he end up eating his shirt?
Schnorr is 78 years old. I am not gerontophobic (being 50 I am approaching that age) but: Atiyah claimed the Riemann Hypothesis, Hironaka has claimed full resolution of singularities in any characteristic... And I am speaking of Fields medalists.
So: you do really need peer-review for strong arguments.
You might wonder how people find bugs. Low-hanging fruit bugs can be found via code review, static analysis, dynamic analysis (like fuzzing), and other techniques. But what about deep logic bugs. Those you can’t find easily. Perhaps the protocol implemented is quite complicated, or correctness is hard to define, and edge-cases hard to detect. One thing I’ve noticed is that re-visiting protocols are an excellent way to find logic bugs.
Ian Miers once said something like that: "you need time, expertise, and meaningful engagement”. I like that sentence, although one can point out that these traits are closely linked--you can’t have meaningful engagement without time and expertise--it does show that finding bugs take "effort".
OK. Meaningful engagement can lead to meaningful bugs, and meaningful bugs can be found at different levels.
So you're here, seating in your undies in the dark, with a beer on your side and some uber eats lying on the floor.
Your computer is staring back at you, blinking at a frequency you can't notice, and waiting for you to find a bug in this protocol.
What do you do?
Perhaps the protocol doesn't have a proof, and this leads you to wonder if you can write one for it...
It worked for Ariel Gabizon, who in 2018 found a subtle error in a 2013 zk-SNARK paper used by the Zcash cryptocurrency he was working on.
He found it by trying to write a proof for the paper he was reading, realizing that the authors had winged it.
While protocols back in the days could afford to wing it, these days people are more difficult--they demand proofs.
The bug Ariel found could have allowed anyone to forge an unlimited amount of money undetected.
It was silently fixed months later in an upgrade to the network.
Ariel Gabizon, a cryptographer employed by the Zcash Company at the time of discovery, uncovered a soundness vulnerability. The key generation procedure of [BCTV14], in step 3, produces various elements that are the result of evaluating polynomials related to the statement being proven. Some of these elements are unused by the prover and were included by mistake; but their presence allows a cheating prover to circumvent a consistency check, and thereby transform the proof of one statement into a valid-looking proof of a different statement. This breaks the soundness of the proving system.
What if the protocol already had a proof though?
Well that doesn't mean much, people enjoy writing unintelligible proofs, and people make errors in proofs all the time.
So the second idea is that reading and trying to understand a proof might lead to a bug in the proof.
Here's some meaningful engagement for you.
In 2001, Shoup revisited some proofs and found some darning gaps in the proofs for RSA-OAEP, leading to a newer scheme OAEP+ which was never adopted in practice.
Because back then, as I said, we really didn't care about proofs.
[BR94] contains a valid proof that OAEP satisfies a certain technical property which they call “plaintext awareness.” Let us call this property PA1. However, it is claimed without proof that PA1 implies security against chosen ciphertext attack and non-malleability. Moreover, it is not even clear if the authors mean adaptive chosen ciphertext attack (as in [RS91]) or indifferent (a.k.a. lunchtime) chosen ciphertext attack (as in [NY90]).
Later in 2018, a series of discoveries on the proofs for the OCB2 block cipher quickly led to practical attacks breaking the cipher.
We have presented practical forgery and decryption attacks against OCB2, a high-profile ISO-standard authenticated encryption scheme. This was possible due to the discrepancy between the proof of OCB2 and the actual construction, in particular the interpretation of OCB2 as a mode of a TBC which combines XEX and XE.
We comment that, due to errors in proofs, ‘provably-secure schemes’ sometimes still can be broken, or schemes remain secure but nevertheless the proofs need to be fixed. Even if we limit our focus to AE, we have many examples for this, such as NSA’s Dual CTR [37,11], EAX-prime [28], GCM [22], and some of the CAESAR submissions [30,10,40]. We believe our work emphasizes the need for quality of security proofs, and their active verification.
Now, reading and verifying a proof is always a good idea, but it’s slow, it’s not flexible (if you change the protocol, good job changing the proof), and it’s limited (you might want to prove different things re-using parts of the proofs, which is not straight forward).
Today, we are starting to bridge the gap between pen and paper proofs and computer science: it is called formal verification.
And indeed, formal verification is booming, with a number of papers in the recent years finding issues here and there just by describing protocols in a formal language and verifying that they withstand different types of attacks.
Prime, Order Please! Revisiting Small Subgroup and Invalid Curve Attacks on Protocols using Diffie-Hellman:
We implement our improved models in the Tamarin prover. We find a new attack on the Secure Scuttlebutt Gossip protocol, independently discover a recent attack on Tendermint’s secure handshake, and evaluate the effectiveness of the proposed mitigations for recent Bluetooth attacks.
Seems Legit: Automated Analysis of Subtle Attacks on Protocols that Use Signatures:
We implement our models in the Tamarin Prover, yielding the first way to perform these analyses automatically, and validate them on several case studies. In the process, we find new attacks on DRKey and SOAP’s WS-Security, both protocols which were previously proven secure in traditional symbolic models.

But even this kind of techniques has limitation! (OMG David when will you stop?)
In 2017 Matthew Green wrote:
I don’t want to spend much time talking about KRACK itself, because the vulnerability is pretty straightforward. Instead, I want to talk about why this vulnerability continues to exist so many years after WPA was standardized. And separately, to answer a question: how did this attack slip through, despite the fact that the 802.11i handshake was formally proven secure?
He later writes:
The critical problem is that while people looked closely at the two components — handshake and encryption protocol — in isolation, apparently nobody looked closely at the two components as they were connected together. I’m pretty sure there’s an entire geek meme about this.
pointing to the "2 unit tests. 0 integration tests." joke.

He then recognizes that it’s a hard problem:
Of course, the reason nobody looked closely at this stuff is that doing so is just plain hard. Protocols have an exponential number of possible cases to analyze, and we’re just about at the limit of the complexity of protocols that human beings can truly reason about, or that peer-reviewers can verify. The more pieces you add to the mix, the worse this problem gets.
In the end we all know that the answer is for humans to stop doing this work. We need machine-assisted verification of protocols, preferably tied to the actual source code that implements them. This would ensure that the protocol actually does what it says, and that implementers don’t further screw it up, thus invalidating the security proof.
Well, Matthew, we do have formally generated code! HACL* and fiat-crypto are two examples.
Anybody has heard of that failing? I’d be interested…
In any case, what’s left for us? A lot! Formally generated code is hard, and generally covers small parts of your protocol (e.g. field arithmetic for elliptic curves).
So what else can we do?
Implementing the protocol, if it hasn’t been implemented before, is a no-brainer.
In 2016, Taylor Hornby an engineer at Zcash wrote about a bug he found while implementing the zerocash paper into the Zcash cryptocurrency:
In this blog post, we report on the security issues we’ve found in the Zcash protocol while preparing to deploy it as an open, permissionless financial system.
Had we launched Zcash without finding and fixing the InternalH Collision vulnerability, it could have been exploited to counterfeit currency. Someone with enough computing power to find 128-bit hash collisions would have been able to double-spend money to themselves, creating Zcash out of thin air.
Perhaps re-implementing the protocol in a different language might work as well?
One last thing, most of the code out there is not formally verified.
So of course, reviewing code works, but you need time, expertise, money, etc.
So instead, what about testing?
This is what Wycheproof does by implementing a number of test vectors that are known to cause issues:
These observations have prompted us to develop Project Wycheproof, a collection of unit tests that detect known weaknesses or check for expected behaviors of some cryptographic algorithm. Project Wycheproof provides tests for most cryptographic algorithms, including RSA, elliptic curve crypto and authenticated encryption. Our cryptographers have systematically surveyed the literature and implemented most known attacks. We have over 80 test cases which have uncovered more than 40 bugs. For example, we found that we could recover the private key of widely-used DSA and ECDHC implementations.
In all of that, I didn't even talk about the benefits of writing a specification... that's for another day.
If you didn't know, I've been writing a book (called Real-World Cryptography) for almost 2 years now on applied cryptography, why would I do this? I answered this in a post here.
I've finished writing all 15 chapters which are split into a first part on primitives, the ingredients of cryptography, and a second part on protocols, the recipes of cryptography:
- Introduction
- Hash functions
- Message authentication codes
- Authenticated encryption
- Key exchanges
- Asymmetric encryption and hybrid encryption
- Signatures and zero-knowledge proofs
- Randomness and secrets
- Secure transport
- End-to-end encryption
- User authentication
- Crypto as in cryptocurrency?
- Hardware cryptography
- Post-quantum cryptography
- Next-generation cryptography and final words
Is this it? Unfortunately it is not, I now will start the long revision process. I am collecting feedback on various chapters, so if you want to help me write the best book possible please contact me with a chapter in mind :)
warning: some errors got into this post. If you're following it to the letter they might be confusing to you. Note that they have been fixed in the book.
In part 1 of this series I explained what exactly zk-SNARKs attempt to prove. The answer was confusing: zk-SNARKs are surely efficient at proving things, but they’re only useful at proving that you know a polynomial constrained by some known roots. How is that useful for us? How does one uses such a system to prove more general statements? This is what I will answer in the second part of this series. Make sure that you read part 1 before getting into this, as this won’t make too much sense otherwise :)
From programs to polynomials
So far the constraints on the polynomial that the prover must find is that it has some roots (some values that evaluate to 0 with our polynomial). But how do we translate a more general statement into a polynomial knowledge proof? Typical statements in cryptocurrencies (which are the applications currently making the most use of zk-SNARKs these days) are of the form:
- prove that a value is in the range $[0, 2^64)$ (this is called a range proof)
- prove that a (secret) value is included in some given (public) Merkle tree
- prove that the sum of some values is equal to the sum of some other values
- etc.
And here is the difficult part… as I said in part 1 of this series, converting a program execution into the knowledge of a polynomial “sorts of requires a graduate course into the subject”. The good news is that I’m not going to tell you all about the details, but give you enough to give you a sense of how things work. From there, you should be able to understand what are the parts that are missing from my explanation and fill in the gaps as you wish.
A program to an arithmetic circuits
First, let’s acknowledge that any program can be re-written (more or less easily) in math. The reason why we would want to do that should be obvious: we can’t prove code, but we can prove math.
For example, let’s take the following function where every input is public except for a which is our secret input:
fn my_function(w, a, b) {
if w == true {
return a + b;
} else {
return a x b;
}
}
In this simple example, if every input and output is public except for a, one can still deduce what a is. So this example also serves as an example of what you shouldn’t try to prove in zero-knowledge. Anyway, the program can be re-written in math with this equation:
$$
w(a+b) + (1-w)(ab) = v
$$
Where $v$ is the output and $w$ is either $0$ (false) or $1$ (true). Notice that we this equation is not really a program or a circuit, it just looks like a constraint: if you execute the program correctly, and then fill in the different inputs given and outputs obtained in the equation, the equality should be correct.
That’s one mental step we need to take: instead of executing a function in zero-knowledge (which doesn’t mean much really), what we can do is use zk-SNARKs to prove that some given inputs and outputs (secret or public) correctly match the execution of a program.
In any case, we’re only one step into the process of converting our execution to something we can prove with zk-SNARKs, the next step is to convert that in a series of constraints that can be converted in the knowledge of a polynomial. What zk-SNARKs want is a rank-1 constraint system (R1CS). R1CS are really just a series of equations that are of the form $L \times R = O$ where $L, R, O$ can only be the addition of some variables, thus the only multiplication is between $L$ and $R$. It really doesn’t matter why we need to transform our arithmetic circuit into such a system of equations, besides that it helps doing the conversion to the final stuff we can prove.
Try to do this with the equation we have, and we can obtain something like
- $a \times b = m$
- $w \times (m - a - b) = v - a - b$
We actually forgot the constraint that $w$ is either $0$ or $1$, which we can add to our system via a clever trick:
- $a \times b = m$
- $w \times (m - a - b) = v - a - b$
- $w \times w = w$
Does that make sense? You should really see this system as a set of constraints: if you give me a set of values that you claim match the inputs and outputs of the execution of my program, then I should be able to verify that they also correctly verify these $equalities$. If one of the equality is wrong, then it must mean that the program does not output the value you gave me for the inputs you gave me.
Another way to think about it is that zk-SNARKs allow you to verifiably remove inputs or outputs of the transcript of a correct execution of a program.
R1CS to a polynomial
The question now is: how do we transform this system into a polynomial? With a series of tricks!
Since we have three different equations in our system, the first step is to agree on three roots for our polynomial.
We can simply choose $1, 2, 3$ as roots. Meaning that our polynomial solves $f(x) = 0$ for $x = 1$, $x = 2$, and $x = 3$.
Why do that? So that we can make our polynomial represent all the equations in our system at the same time, by representing the first equation when evaluated at $1$, and representing the second equation when evaluated at $2$, and so on. So the prover’s job is now to create a polynomial $f(x)$ such that:
- $f(1) = a \times b - m$
- $f(2) = w \times (m - a - b) - (v - a -b)$
- $f(3) = w \times w - w$
And notice that all these equations should evaluate to $0$ if the values correctly match an execution of our original program. In other words, our polynomial $f(x)$ has roots $1, 2, 3$ only if we created it correctly. And this is all what zk-SNARKs are about if you remember part 1 of this blog series, we have the protocol to prove that our polynomial $f(x)$ indeed has these roots (that were decided during the set up phase of our protocol).
It would be too simple if this is was the end of my explanation, because now the problem is that the prover has way too much freedom in choosing their polynomial $f(x)$, they can simply find a polynomial that has roots $1, 2, 3$ without caring about the values $a, b, m, v, w$. They can do pretty much whatever they want. What we want is a system that locks every parts of the polynomial except for the secret values that the verifier must not learn about.
It takes two to evaluate a polynomial hiding in the exponent
Let's recap:
- We want a prover that has to correctly execute the program with their secret value $a$ and the public values $b$ and $w$ and obtain the output $v$ that they can publish.
- The prover then must create a polynomial by only filling the parts that the verifier must not learn about: the values $a$ and $m$.
Thus, in a real zk-SNARK protocol you want the prover to have the least amount of freedom possible when they create their polynomials and then evaluate it to a random point (as seen in the first part of this blogpost series).
To do this, the polynomial is created somewhat dynamically by having the prover only fill in their part, and having the verifier fill in the other parts.
For example, let’s take the first equation $f(1) = a \times b - m$ and represent it as $f_1(x) = aL_1(x) \times bR_1(x) - mO_1(x)$ where $L_1(x), R_1(x), O_1(x)$ are polynomials that evaluate to $1$ for $x=1$ and to 0 for $x=2, 3$. This is necessary so that they only influence our first equation, and it is easy to use algorithms like Lagrange Interpolation to find such polynomials. Notice two things:
- We now have the inputs, intermediate values, and outputs, as coefficients of our polynomials.
- The polynomial $f(x)$ is the sum $f_1(x) + f_2(x) + f_3(x)$ where we can define $f_2(x)$ and $f_3(x)$ to represent equations 2 and 3, similarly to $f_1(x)$.
The prover can then:
- take the exponentiation of the random point $r$ hidden in the exponent to reconstruct the polynomials $L_1(r)$ and $O_1(r)$
- exponentiate $g^{L_1(r)}$ with the secret value $a$ to obtain $(g^{L_1(r)})^a=g^{aL_1(r)}$ which represents $a \times L_1(x)$ evaluated at the unknown and random point $x=r$ (and hidden in the exponent).
- Multiply $g^{O_1(r)}$ with $g^{m}$ to obtain $g^{O_1(r)}g^{m}=g^{O_1(r)+m}$ which represents the hidden evaluation of $O_1(x) + m$ at the random point $r$ (and hidden in the exponent).
And then the verifier can fill in the missing parts:
- reconstruct $g^{bR_1(x)}$ for some value $b$ and using the same techniques the prover used
- reconstruct $f_1(r)$ by using a bilinear pairing (seen in part 1 of this blog post series) as such: $f_1(r) = e(g^{aL(r)}, g^{bR(r)}) - e(g, g^{O(r) + m}) = e(g, g)^{aL(r) \times bR(r)} - e(g,g)^{O(r) + m}$
If you extrapolate these techniques to the whole polynomial $f(x)$ you can figure out the final protocol.
Of course, this is still a gross simplification of a real zk-SNARK protocol, my explanations still leave way too much power to the prover. All the other tricks that you can learn about are meant to restrict what the prover can do, ensuring that they correctly and consistently fill in the missing parts, and optimizing what can be optimized.
I want to know more
I learned everything in the tutorial Why and How zk-SNARK Works: Definitive Explanation which goes much more in depth and explains all of parts that I’ve overlooked.
And if you like this content, be sure to check my book real-world cryptography.






