Quick access to articles on this page:
more on the next page...
What are ZK-SNARKs and how do they work? This is a question I’ve had for years, and always felt like the resources I found gave no clear intuition as to how all of that stuff worked. So today, after a breakthrough in my own understanding, I thought it would be good to re-share what I’ve learned in a more understandable picture. Something that tells you what is the right way of thinking about these things, and what are the gaps that you can fill for yourself if you want to.
Getting terminology out of the way
The first part of the question is pretty easy to answer. ZK-SNARKs, no matter what their funny name might imply, are simply zero-knowledge proofs that are:
- non interactive
- general purpose
- and succinct
Huh, what are all these words? you ask, intimidated by their vagueness.
Well first, zero-knowledge proofs are cryptographic proofs that you know something, without revealing the something (zero-knowledgeness). That “something” is usually called the witness, but this detail doesn’t matter much. There are a lot of resources about zero-knowledge proofs so I won’t explain much about how they work, or what their exact cryptographic properties are (completeness, soundness, zero-knowledgeness).
Zero-knowledge proofs are often seen used to prove that you know the discrete logarithm in some base of an element of some group (e.g. what is $x$ in $g^x \mod p$), or similarly-limited statements.
“Limited yes, but still useful!” yells Schnorr, inventor of the Schnorr signature scheme which is fabricated by taking a zero-knowledge proof of the knowledge of a discrete logarithm, and making it non-interactive. A zero-knowledge proof or ZKP is an interactive protocol between a prover (who knows the witness) and a verifier (who has to be convinced). An interactive protocol sucks in the real world, as it often limits the number of potential use-cases of the primitive, and slows down protocols depending on the number of round trips that need to happen between the prover and the verifier. Fortunately, some ZKPs can be constructed without interaction with a verifier. In other words, a prover can simply create a proof, and that proof can be verified by anyone at any point in time later without further help from the prover. When ZKPs are made non-interactive, we simply call them non-interactive zero-knowledge proofs or NIZKs. I talk more about the link between signatures and zero-knowledge proofs here.
ZKPs and NIZKs can also be constructed on much more general statements like “I know an input to some function such that the execution gives some output”, or more specifically “I know $a$ in $f(a, b) = c$”. If this still doesn’t make sense think about the usual example given to illustrate general-purpose ZKPs: “I know the solution of the sudoku”.
We’re almost there: ZK-SNARKs are general-purpose non-interactive zero-knowledge proofs, and more! They are also succinct, meaning that the proofs they produce are small in size and are fast to verify, which makes them so special they deserve to be called ZK-SNARKs. Not every modern proof systems deserve that special classification, for example STARKs don’t :(
As a recap:
- zero-knowledge proof: a cryptographic proof that you know something, without revealing the something
- non interactive: a proof that was constructed without the help of a verifier
- general purpose: a proof of a more general statement, like the knowledge of secret inputs or outputs of a program
- succinct: a small proof that is fast to verify
But not only did you ask, what are ZK-SNARKs, but you also asked about how they work.
The actual stuff
And oh boy, this is a complex subject to answer. First and foremost, there are many many schemes, too many of them, and so I’m not sure exactly how to answer that question. But I have some idea of how some of them work, and so I imagine that most of them follow that pattern, or improve on it, so let me explain…
There’s two parts to your typical ZK-SNARK:
- The proving system, which I'll explain in this post.
- The translation or compilation of a program to something the proving system can prove, which I'll explain in part 2 of this post.
The first part is not too hard to understand, while the second sort of requires a graduate course into the subject…
Proving your knowledge of a constrained polynomial
Here it is, remember that one: ZK-SNARKs are all about proving that you know some polynomial $f(x)$ that has some roots.
By roots I mean that the verifier has some values in mind (e.g. $1$ and $2$) and the prover must prove that the secret polynomial they have in mind evaluates to $0$ for this values (e.g. $f(1) = f(2) = 0$).
By the way, a polynomial that has 1 and 2 as roots (in our example) can be written as $f(x)=(x-1)(x-2)h(x)$ for some polynomial $h(x)$. (If you’re not convinced try to evaluate that at $x=1$ and $x=2$.)
So we say that the prover must prove that they know an $f(x)$ and $h(x)$ such that $f(x) = t(x)h(x)$ for some target polynomial $t(x) = (x-1)(x-2)$ (in the example that $1$ and $2$ are the roots that the verifier wants to check).
But that’s it, that’s what ZK-SNARKs proving systems usually provide: something to prove that you know some polynomial. I’m repeating this because the first time I learned about that it made no sense to me: how can you prove that you know some secret input to a program, if all you can prove is that you know a polynomial. Well, that’s why part 2 of this explanation is so difficult: it’s about translating a program into a polynomial. But more on that later.
Back to our proving system, how does one prove that they know such a function $f(x)$? Well they just have to prove that they know an $h(x)$ such that you can write $f(x)$ as $f(x) = t(x)h(x)$. Ugh… Not so fast here. We’re talking about zero-knowledge proofs right? How can we prove this without giving out $f(x)$? Well, by using three tricks!
- homomorphic commitments
- bilinear pairings
- different polynomials evaluate to different values most of the time
So let's go through each of them shall we?
Homomorphic commitments
The first trick is to use commitments to hide the values that we’re sending to the prover. But not only do we hide them, we also want to allow the verifier to perform some operations on them so that they can verify the proof. Specifically verify that if the prover commits on their polynomial $f(x)$ as well as $h(x)$, then we have
$$
com(f(x)) = com(t(x)) com(h(x)) = com(t(x)h(x))
$$
where $com(t(x))$ is computed by the verifier as these are the known constraints on the polynomial.
These operations are called homomorphic operations and we can’t perform them if we use hash functions as commitment mechanisms. Instead, we can simply “hide the values in the exponent” (e.g. for a value $v$ then send the commitment $g^v \mod{p}$) as these are commitments that allow for these homomorphic operations. (To convince yourself, observe that if $a = bc$ then $g^a = g^b g^c = g^{b+c}$.
Wait, this is not what we wanted… we wanted $g^a = g^{bc}$.
Bilinear pairings
$g^a = (g^b)^c = g^{bc}$ gets us there, but only if $c$ is a known value and not a commitment (e.g. $g^c$). Unfortunately this is a limitation for our proving protocol, as there will be multiplication operations between commitments. This is where bilinear pairings can be used to unblock us, and this is the sole reason why we use bilinear pairings in a ZK-SNARK (really just to be able to multiply the values inside the commitments).
I don’t want to go too deep into what bilinear pairings are, but just know that it is just another tool in our toolkit that:
- Takes two values of our group (the values generates by $g$ raised to different powers modulo $p$) and place them in another group.
- By moving stuff from one group to the other, we can multiply things that couldn't be multiplied previously.
So using $e$ as the typical way of writing a bilinear pairing, we have $e(g_1, g_2) = h_3$ and we can use it to perform multiplications hidden in the exponent via this one equation:
$$
e(g^b, g^c) = e(g)^{bc}
$$
But no more about bilinear pairings! Again that’s the only reason why we use these in ZK-SNARKs. It’s just a trick to make our homomorphic commitments more homomorphic, to allow us to do:
$$
com(f(x)) = com(t(x)) com(h(x)) = com(t(x)h(x))
$$
Where does the succinctness comes from?
Finally, the succinctness of ZK-SNARKs come from the fact that two functions that differ will evaluate to different points most of the time.
What this means for us is that if my $f(x)$ is not really equal to $t(x)h(x)$, meaning that I don’t have a polynomial $f(x)$ that really has the roots we’ve chosen with the verifier, then evaluating $f(x)$ and $t(x)h(x)$ at a random point $r$ will not give out the same result (most of the time). In other words for almost all $r$, $f(r) \neq t(r)h(r)$.
This is known as the Schwartz-Zippel lemma, which I pictured in the following illustration.
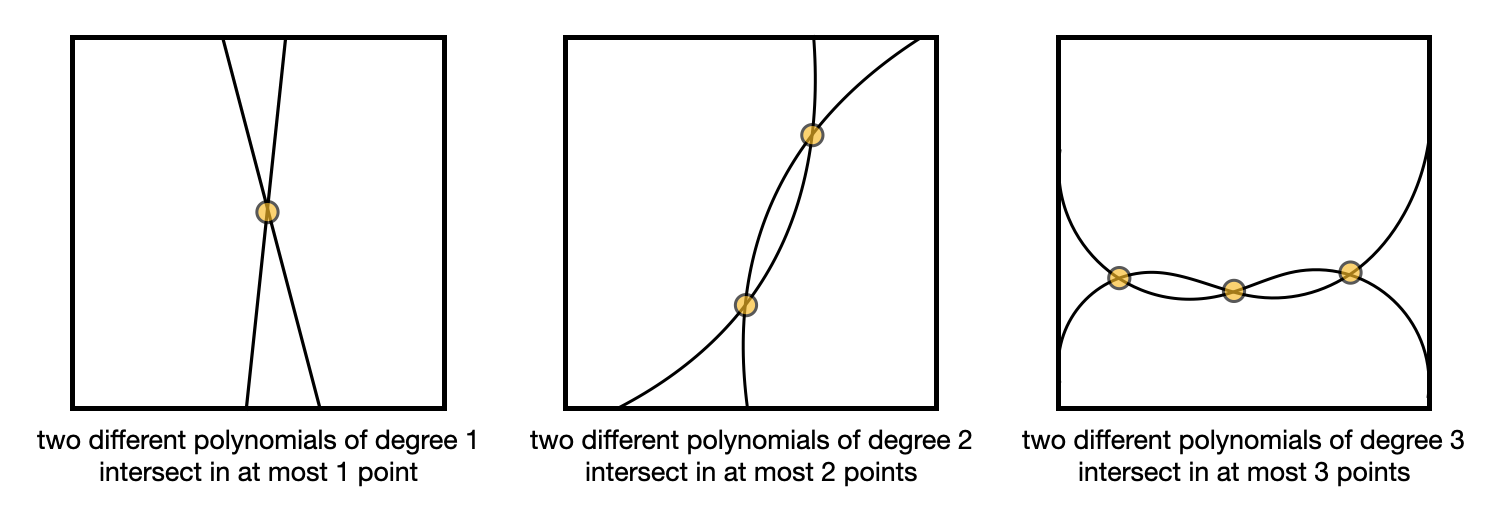
Knowing this, it is enough to prove that $com(f(r)) = com(t(r)h(r))$ for some random point $r$. This is why ZK-SNARKs are so small; by comparing points in a group you end up comparing entire polynomials!
But this is also why there is a “trusted setup” needed before most ZK-SNARKs can work. If a prover learns the random point $r$, then they can forge bad polynomials that will verify. So a trusted setup is about:
- creating a random value $r$
- committing different exponentiation of it $g^r, g^{r^2}, g^{r^3}, \ldots$ so that they can be used by the prover to compute their polynomial without knowing the point $r$
- destroying the value $r$
Does the second point makes sense? If my polynomial as the prover is $f(x) = x^2 + x$ then all I have to do is compute $g^{r^2} g^r$ to obtain a commitment of my polynomial evaluated at that random point $r$.
Part 2 is here.
Lamport says:
I have long felt that, because it was posed as a cute problem about philosophers seated around a table, Dijkstra's dining philosopher's problem received much more attention than it deserves. (For example, it has probably received more attention in the theory community than the readers/writers problem, which illustrates the same principles and has much more practical importance.) I believed that the problem introduced in [41] was very important and deserved the attention of computer scientists. The popularity of the dining philosophers problem taught me that the best way to attract attention to a problem is to present it in terms of a story.
What are all these cute stories in cryptography?
- Alice and Bob
For our scenarios we suppose that A and B (also known as Alice and Bob) are two users of a public-key cryptosystem.
- Dining cryptographers
Three cryptographers are sitting down to dinner at their favorite three-star restaurant. Their waiter informs them that arrangements have been made with the maitre d'hotel for the bill to be paid anonymously. One of the cryptographers might be paying for the dinner, or it might have been NSA (U.S. National Security Agency). The three cryptographers respect each other's right to make an anonymous payment, but they wonder if NSA is paying.
- The fully homomorphic dragon
One night, Alice dreams of immense riches, caverns piled high with silver, gold and diamonds. Then, a giant dragon devours the riches and begins to eat its own tail! She awakes with a feeling of peace. As she tries to make sense of her dream, she realizes that she has the solution to her problem.
- The Byzantine Generals Problem
We imagine that several divisions of the Byzantine army are camped outside an enemy city, each division commanded by its own general. The generals can communicate with one another only by messenger. After observing the enemy, they must decide upon a common plan of action. However, some of the generals may be traitors, trying to prevent the loyal generals from reaching agreement.
- The Zero-Knowledge Cave
- Mental Poker
Once there were two “mental chess ” experts who had become tired of their pastime. “Let’s play ‘Mental Poker, ‘for variety” suggested one. “Sure” said the other. “Just let me deal!”
- The Birthday Attack
In probability theory, the birthday problem or birthday paradox concerns the probability that, in a set of n randomly chosen people, some pair of them will have the same birthday. By the pigeonhole principle, the probability reaches 100% when the number of people reaches 367 (since there are only 366 possible birthdays, including February 29). However, 99.9% probability is reached with just 70 people, and 50% probability with 23 people.
- Yao's millionaire problem
Two millionaires wish to know who is richer; however, they do not want to find out inadvertently any additional information about each other’s wealth. How can they carry out such a conversation?
- Coin Flipping by Phone
Alice and Bob want to flip a coin by telephone. (They have just divorced, live in different cities, want to decide who gets the car.) Bob would not like to tell Alice HEADS and hear Alice (at the other end of the line) say "Here goes... I'm flipping the coin... You lost!"
Do you know of any other story?
I read a Why Not Rust? article the other day that was quite good but dismissed the most important reason to use a language to me: security. After having worked on a Rust codebase for almost two years now, I thought I would chime in, even though I'll preface the post by saying that Rust is totally the right language you should use if you know what you're doing and are aiming for performance and security, yet I still have some pain points that will make me recommend Golang over Rust sometimes. Keep in mind that I have also spent my whole career looking for bugs in applications written in dozens of different languages, so my post might be highly controversial but it has to be looked from these lenses.
Shallow standard library
Working with Rust is like working with Javascript in many ways. While the package manager Cargo is truly awesome, the fact that the standard library misses most features will have you import many third-party dependencies. These dependencies in turn import other third-party dependencies, that import other third-party dependencies, and so on. This blow up of dependencies can quickly become a nightmare, and this is of course a perfect vector of attack for backdoors, like we've seen happen before in javascript land (https://www.infoq.com/news/2018/05/npm-getcookies-backdoor/, https://www.zdnet.com/article/hacker-backdoors-popular-javascript-library-to-steal-bitcoin-funds/).
Not only this, but if you're a newcomer to Rust, how do you even pick the right library? I can't even fathom how anyone writing a project in Rust gets to pick a good library for generating cryptographic random numbers, or for doing any type of crypto like encrypting or hashing, or for decoding hex strings, or for decoding JSON, or for using TCP, or even for using TLS! On the other hand Golang has all of that in its standard library, that means that when you use Golang you:
- can't pick the wrong algorithm (e.g. DES instead of AES)
- can't pick a bad implementation (the standard library is known to be high quality)
- can't pick a dependency that ends up importing plenty of other third-party dependencies (unlike Rust, the Golang standard library never imports third-party libraries)
- don't have to worry about version updates (you're just updating your version of Golang instead of the versions of many dependencies)
- don't have to worry about transitive dependencies that you can't update (again, Golang standard library doesn't rely on third-party dependencies)
For Libra we've used a number of techniques in order to reduce the number of third-party dependencies we use. This included figuring out when we used different dependencies that did the same thing, or figuring out what obscure dependencies we should avoid, we even re-wrote a large number of dependencies to avoid dependencies that ended up exploding the number of transitive third-party dependencies we imported. One useful tool we used for some of that is dephell which is built on top of guppy.
Rustfmt is imperfect
rustfmt is great, but rustfmt sucks. Why does it suck? Two reasons:
- it's not mandatory
- it's configurable
On the other hand, Golang's compiler is very strict and will yell at you early on if you have dead code, unused dependencies, badly formatted code, and so on. It doesn't replace gofmt, but it's much more opinionated and is much more effective at making Golang's codebases more readable (especially if they forget to run gofmt). In addition, if you do use gofmt, you can't configure it! This is very apparent when you read Golang code, it always looks the same! And it is pretty fucking fantastic if you ask me, because not only Golang is easy to learn, but you can quickly get used to any Golang codebase due to the consistent formatting of the language.
Too many ways to do things
Rust has a somewhat different syntax from other languages of its genre, and you sometimes see things that you might not be used to see (statement as expression, match statements, lifetimes, etc.) I couldn't care less about these, these are things you can learn, and you end up getting used to them. What I can't get used to is the sheer number of ways to do something. There are so many keywords in Rust, and there's so many ways to end up bike shedding on the best way to write the exact same statement, that I consider it a waste of time. It's a waste of time for the developers, but also for the reviewers who will often run into keywords that they've never seen before. For example, there are too many ways to panic on purpose: panic!(), unwrap(), except(), unreachable!(), todo!(), unimplemented!(), assert!(), and so on.
Generics and macros
Rust is too expressive. This is of course great for some use-cases, but holy shit if a developer wants to be too clever, they can create the most unintelligible codebase that you'll ever seen. This is probably the most controversial point, but security is not just safety, it's also readability. As we say "complexity is the enemy of security", and generics undeniably add complexity. This is of course up to the developers to abuse them, but the great thing about Golang is that there aren't many things to abuse, codebases are often straight forward and you can quickly understand what is happening.
Ok, you're being unreasonable David
Sure, I'm omitting a lot of good Rust things in here, but this is a post about the security downsides of Rust, not the upsides, which let's be clear still make Rust the perfect language to write a sensitive application in. You just need to know what you're doing. This also means that Rust has a lot of room to mature, while generics are here to stay, there is no excuse to keep slipping the shallow stdlib under the rug.
I’ve now been writing a book on applied cryptography for a year and a half.
I’m nearing the end of my journey, as I have one last ambitious chapter left to write: next-generation cryptography (a chapter that I’ll use to talk about cryptography that will become more and more practical: post-quantum cryptography, homomorphic encryption, multi-party computation, and zk-SNARKs).
I’ve been asked multiple times why write a new book about cryptography? and why should I read your book?.
To answer this, you have to understand when it all started…
A picture is worth a thousand words
Today if you want to learn about almost anything, you just google it.
Yet, for cryptography, and depending on what you're looking for, resources can be quite lacking.
It all started a long time ago.
For a class, I had to implement a differential power analysis attack, a breakthrough in cryptanalysis as it was the first side-channel attack to be published.
A differential power analysis uses the power consumption of a device during an encryption to leak its private key.
At the time, I realized that great papers could convey great ideas with very little emphasis on understanding.
I remember banging my head against the wall trying to figure out what the author of the white paper was trying to say.
Worse, I couldn’t find a good resource that explained the paper.
So I banged my head a bit more, and finally I got it.
And then I thought I would help others.
So I drew some diagrams, animated them, and recorded myself going over them.
That was my first screencast.
This first step in education was enough to make me want to do more.
I started making more of these videos, and started writing more articles about cryptography on this blog (today totaling more than 500 articles).
I realized early that diagrams were extremely helpful to understand complicated concepts, and that strangely most resources in the field shied away from them.
For example, anyone in cryptography who thinks about AES-CBC would immediately think about the following wikipedia diagram:
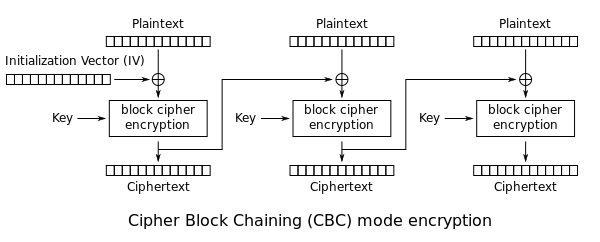
So here I was, trying to explain everything I learned, and thinking hard about what sorts of simple diagrams could easily convey these complex ideas.
That’s when I started thinking about a book, years and years before Manning Publications would reach out to me with a book deal.
The applied cryptographer curriculum
I hadn’t started cryptography due to a long-life passion.
I had finished a bachelor in theoretical mathematics and didn’t know what was next for me.
I had also been programming my whole life, and I wanted to reconcile the two.
Naturally, I got curious about cryptography, which seemed to have the best of both world, and started reading the different books at my disposal.
I quickly discovered my life's calling.
Some things were annoying me though. In particular, the long introductions that would start with history.
I was only interested in the technicalities, and always had been.
I swore to myself, if I ever wrote a book about cryptography, I would not write a single line on Vigenère ciphers, Caesar ciphers, and others.
And so after applying to the masters of Cryptography at the university of Bordeaux, and obtaining a degree in the subject, I thought I was ready for the world.
Little did I know.
What I thought was a very applied degree actually lacked a lot on the real world protocols I was about to attack.
I had spent a lot of time learning about the mathematics of elliptic curves, but nothing about how they were used in cryptographic algorithms.
I had learned about LFSRs, and ElGamal, and DES, and a series of other cryptographic primitives that I would never see again.
When I started working in the industry at Matasano, which then became NCC Group, my first gig was to audit OpenSSL (the most popular TLS implementation).
Oh boy, did it hurt my brain.
I remember coming back home every day with a strong headache.
What a clusterfuck of a library.
I had no idea at the time that I would years later become a co-author of TLS 1.3.

But at that point I was already thinking: this is what I should have learned in school.
The knowledge I’m getting now is what would have been useful to prepare me for the real world.
After all, I was now a security practitioner specialized in cryptography.
I was reviewing real-world cryptographic applications.
I was doing the job that one would wish they had after finishing a cryptography degree.
I implemented, verified, used, and advised on what cryptographic algorithms to use.
This is the reason I’m the first reader of the book I’m writing.
This is what I would have written to my past self in order to prepare me for the real world.
The use of cryptography is where most of the bugs are
My consulting job led me to audit many real world cryptographic applications like the OpenSSL, the encrypted backup system of Google, the TLS 1.3 implementation of Cloudflare, the certificate authority protocol of Let’s Encrypt, the sapling protocol of Zcash, the threshold proxy re-encryption scheme of NuCypher and dozens and dozens of other real-world cryptographic applications that I unfortunately cannot mention publicly.
Early in my job, I was tasked to audit the custom protocol a big corporation (that I can’t name) had written to encrypt their communications.
It turns out that, they were signing everything but the ephemeral keys, which completely broke the whole protocol (as one could have easily replaced the ephemeral keys).
A rookie mistake from anyone with some experience with secure transport protocols, but something that was missed by people who thought they were experienced enough to roll their own crypto.
I remember explaining the vulnerability at the end of the engagement, and a room full of engineers turning silent for a good 30 seconds.
This story repeated itself many times during my career.
There was this time where while auditing a cryptocurrency for another client, I found a way to forge transactions from already existing ones (due to some ambiguity of what was being signed).
Looking at TLS implementations for another client, I found some subtle ways to break an RSA implementation, which in turned transformed into a white paper (with one of the inventor of RSA) leading to a number of Common Vulnerabilities and Exposures (CVEs) reported to a dozen of open source projects.
More recently, reading about Matrix as part of writing my book, I realized that their authentication protocol was broken, leading to a break of their end-to-end encryption.

There’s so many details that can unfortunately collapse under you, when making use of cryptography.
At that point, I knew I had to write something about it.
This is why my book contains many of these anecdotes.
As part of the job, I would review cryptography libraries and applications in a multitude of programming languages.
I discovered bugs (for example CVE-2016-3959 in Golang’s standard library), I researched ways that libraries could fool you into misusing them (for example see my paper How to Backdoor Diffie-Hellman), and I advised on what libraries to use.
Developers never knew what library to use, and I always found the answer to be tricky.
I went on to invent the disco protocol, and wrote a fully-featured cryptographic library in less than 1,000 lines of code in several languages.
Disco only relied on two cryptographic primitives: the permutation of SHA-3 and curve25519.
Yes, from only these two things in 1,000 lines of code a developer could do any type of authenticated key exchange, signatures, encryption, MACs, hashing, key derivation, etc.
This gave me a unique perspective as to what a good cryptographic library was supposed to be.
I wanted my book to contain these kind of practical insights.
So naturally, the different chapters contain examples on how to do crypto in different programming languages, using well-respected cryptographic libraries.
A need for a new book?
As I was giving one of my annual cryptography training at Black Hat, one student came to me and asked if I could recommend a good book or online course on cryptography.
I remember advising the student to read the book from Boneh & Shoup and Cryptography I from Boneh on Coursera.
The student told me “Ah, I tried, it’s too theoretical!”.
This answer stayed with me.
I disagreed at first, but slowly realized that they were right.
Most of these resources were pretty heavy in math, and most developers interacting with cryptography don’t want to deal with math.
What else was there for them?
The other two somewhat respected resources at the time were Applied Cryptography and Cryptography Engineering (both from Schneier).
But these books were starting to be quite outdated.
Applied Cryptography spent 4 chapters on block ciphers, with a whole chapter on cipher modes of operation but none on authenticated encryption.
Cryptography Engineering had a single mention of elliptic curve cryptography (in a footnote).
On the other hand, many of my videos or blog posts were becoming good primary references for some cryptographic concepts.
I knew I could do something special.
Gradually, many of my students started becoming interested in cryptocurrencies, asking more and more questions on the subject.
At the same time, I started to audit more and more cryptocurrency applications.
I finally moved to a job at Facebook to work on Libra.
Cryptocurrency was now one of the hottest field to work on, mixing a multitude of extremely interesting cryptographic primitives that so far had seen no real-world use case (zero knowledge proofs, aggregated signatures, threshold cryptography, multi-party computations, consensus protocols, cryptographic accumulators, verifiable random functions, verifiable delay functions, ... the list goes on)
I was now in a unique position.
I knew I could write something that would tell students, developers, consultants, security engineers, and others, what modern applied cryptography was all about.

This was going to be a book with very little formulas, but filled with many diagrams.
This was going to be a book with little history, but filled with modern stories about cryptographic failures that I had witnessed for real.
This was going to be a book with little about legacy algorithms, but filled with cryptography that I've personally seen being used at scale: TLS, the Noise protocol framework, Wireguard, the Signal protocol, cryptocurrencies, HSMs, threshold cryptography, and so on.
This was going to be a book with little theoretical cryptography, but filled with what could become relevant: password-authentication key exchanges, zero-knowledge proofs, post-quantum cryptography, and so on.
Real-World Cryptography
When Manning Publications reached out to me in 2018, asking if I wanted to write a book on cryptography for them, I already knew the answer.
I already knew what I wanted to write about.
I had just been waiting for someone to give me the opportunity, the excuse to spend my time writting the book I had in mind.
Coincidentally, they had a series of "real-world" book, and so naturally I suggested that my book extend it.

Real-World Cryptography is available for free in early-access.
I want this to be the best book on applied cryptography.
For this reason, if you have any feedback to give, please send it my way :)
The book should be ready in print for the end of the year.
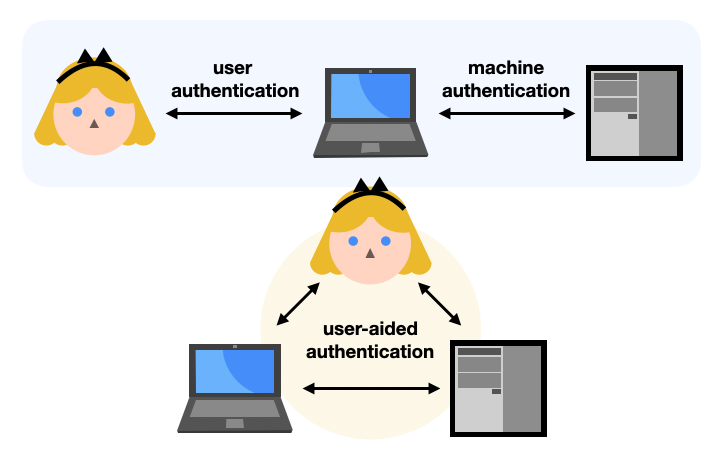
The Secure Remote Password (SRP) protocol is first and foremost a Password Authenticated Key Exchange (PAKE).
Specifically, SRP is an asymmetric or augmented PAKE: it’s a key exchange where only one side is authenticated thanks to a password. This is usually useful for user authentication protocols. Theoretically any client-server protocol that relies on passwords (like SSH) could be doing it, but instead such protocols often have the password directly sent to the server (hopefully on a secure connection). As such, asymmetric PAKEs offer an interesting way to augment user authentication protocols to avoid the server learning about the user’s password.
Note that the other type of PAKE is called a symmetric or balanced PAKE. In a symmetric PAKE two sides are authenticated thanks to the same password. This is usually useful in user-aided authentication protocols where a user attempts to pair two physical devices together, for example a mobile phone or laptop to a WiFi router. (Note that the recent WiFi protocol WPA3 uses the DragonFly symmetric PAKE for this.)
In this blog post I will answer the following questions:
- What is SRP?
- How does SRP work?
- Should I use SRP today?
What is SRP?
The stanford SRP homepage puts it in these words:
The Secure Remote Password protocol performs secure remote authentication of short human-memorizable passwords and resists both passive and active network attacks. Because SRP offers this unique combination of password security, user convenience, and freedom from restrictive licenses, it is the most widely standardized protocol of its type, and as a result is being used by organizations both large and small, commercial and open-source, to secure nearly every type of human-authenticated network traffic on a variety of computing platforms.
and goes on to say:
The SRP ciphersuites have become established as the solution for secure mutual password authentication in SSL/TLS, solving the common problem of establishing a secure communications session based on a human-memorized password in a way that is crytographically sound, standardized, peer-reviewed, and has multiple interoperating implementations. As with any crypto primitive, it is almost always better to reuse an existing well-tested package than to start from scratch.
But the Stanford SRP homepage seems to date from the late 90s.
SRP was standardized for the first time in 2000 in RFC 2944 - Telnet Authentication: SRP.
Nowadays, most people refer to SRP as the implementation used in TLS. This one was specified in 2007 in RFC 5054 - Using the Secure Remote Password (SRP) Protocol for TLS Authentication.
How does SRP work?
The Stanford SRP homage lists 4 different versions of SRP, with the last one being SRP 6. Not sure where version 4 and 5 are, but version 6 is the version that is standardized and implemented in TLS. There is also the revision SRP 6a, but I’m also not sure if it’s in use anywhere today.
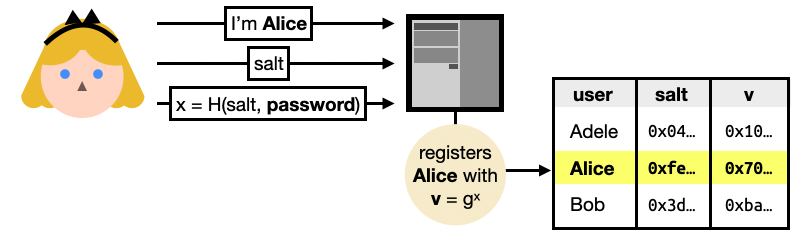
To register, Alice sends her identity, a random $salt$, and a salted hash $x$ of her password.
Right from the start, you can see that a hash function is used (instead of a password hash function like Argon2) and thus anyone who sees this message can efficiently brute-force the hashed password. Not great. The use of the user-generated salt though, manage to prevent brute-force attacks that would impact all users.
The server can then register Alice by exponentiating a generator of a pre-determined ring (an additive group with a multiplicative operation) with the hashed password. This is an important step as you will see that anyone with the knowledge of $x$ can impersonate Alice.
What follows is the login protocol:
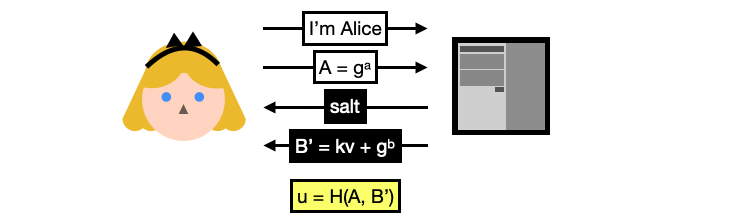
You can now see why this is called a password authenticated key exchange, the login flow includes the standard ephemeral key exchange with a twist: the server’s public key $B’$ is blinded or hidden with $v$, a random value derived from Alice’s password. (Note here $k$ is a constant fixed by the protocol so we will just ignore it.)
Alice can only unblinds the server’s ephemeral key by deriving $v$ herself. To do this, she needs the $salt$ she registered with (and this is why the server sends it back to Alice as part of the flow).
For Alice, the SRP login flow goes like this:
- Alice re-computes $x = H(salt, password)$ using her password and the salt received from the server.
- Alice unblinds the server’s ephemeral key by doing $B=B’- kg^x = g^b$
- Alice then computes the shared secret $S$ by multiplying the results of two key exchanges:
- $B^a$, the ephemeral key exchange
- $B^{ux}$, a key exchange between the server’s public key and a value combining the hashed password and the two ephemeral public keys
Interestingly, the second key exchange makes sure that the hashed password and the transcript gets involved in the computation of the shared secret. But strangely, only the public keys and not the full transcript are used.
The server can then compute the shared secret $S$ as well, using the multiplication of the same two key exchanges:
- $A^b$, the ephemeral key exchange
- $v^{ub}$, the other key exchange involving the hashed password and the two ephemeral public keys
The final step is for both sides to hash the shared secret and use it as the session key $K = H(S)$.
Key confirmation can then happen after both sides make successful use of this session key. (Without key confirmation, you’re not sure if the other side managed to perform the PAKE.)
Should I use SRP today?
The SRP scheme is a much better way to handle user passwords, but it has a number of flaws that make the PAKE protocol less than ideal. For example, someone who intercepts the registration process can then easily impersonate Alice as the password is never directly used in the protocol, but instead the salted hash of the password which is communicated during the registration process.
This was noticed by multiple security researchers along the years. Matthew Green in 2018 wrote Should you use SRP?, in which he says:
Lest you think these positive results are all by design, I would note that there are [five prior versions] of the SRP protocol, each of which contains vulnerabilities. So the current status seems to have arrived through a process of attrition, more than design.
After noting that the combination of multiplication and addition makes it impossible to implement in elliptic curve groups, Matthew Green concludes with:
In summary, SRP is just weird. It was created in 1998 and bears all the marks of a protocol invented in the prehistoric days of crypto. It’s been repeatedly broken in various ways, though the most recent [v6] revision doesn’t seem obviously busted — as long as you implement it carefully and use the right parameters. It has no security proof worth a damn, though some will say this doesn’t matter (I disagree with them.)
Furthermore, SRP is not available in the last version of TLS (TLS 1.3).
Since then, many schemes have been proposed, and even standardized and productionized (for example PAK was standardized by Google in 2010)
The IETF 104, March 2019 - Overview of existing PAKEs and PAKE selection criteria has a list:

In the summer of 2019, the Crypto Forum Research Group (CFRG) of the IETF started a PAKE selection process, with goal to pick one algorithm to standardize for each category of PAKEs (symmetric/balanced and asymmetric/augmented):

Two months ago (March 20th, 2020) the CFRG announced the end of the PAKE selection process, selecting:
- CPace as the symmetric/balanced PAKE (from Björn Haase and Benoît Labrique)
- OPAQUE as the asymmetric/augmented PAKE (from Stanislaw Jarecki, Hugo Krawczyk, and Jiayu Xu)
Thus, my recommendation is simple, today you should use OPAQUE!
If you want to learn more about OPAQUE, check out chapter 11 of my book real world cryptography.
As part of my book's chapter on end-to-end encryption I've been writing about the horrors of PGP.
As a recap of what's bad with PGP:
- No authenticated encryption. This is my biggest issue with PGP personally.
- Receiving a signed message means nothing about who sent it to you (see picture below).
- Usability issues with GnuPG (the main implementation).
- Discoverability of public keys issue.
- Bad integration with emails.
- No forward secrecy.
For more, see my post on a history of end-to-end encryption and the death of PGP.
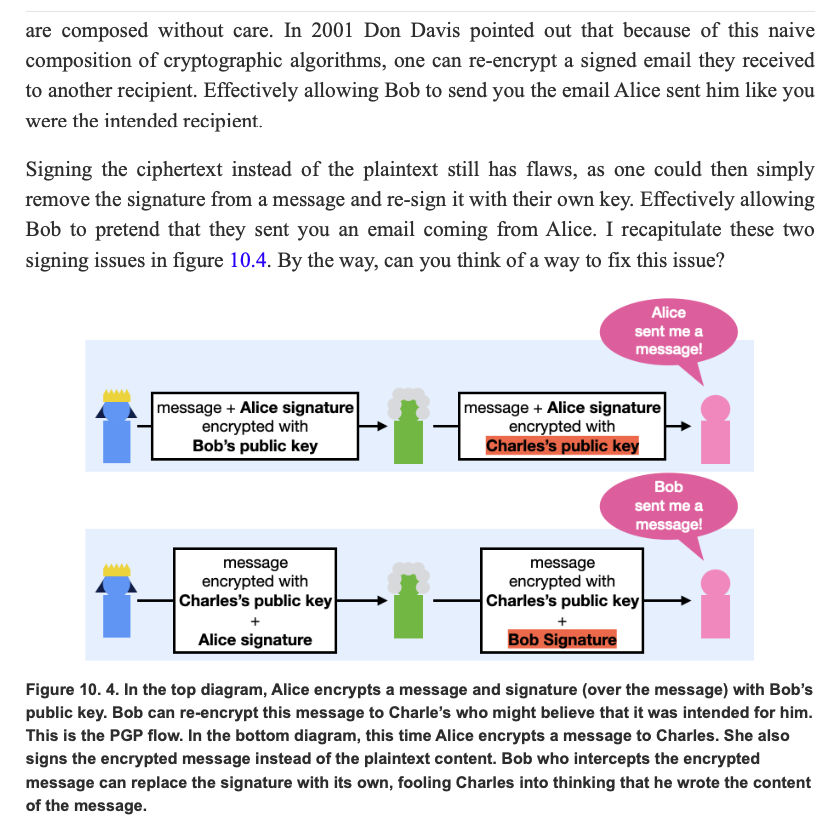
(excerpt from the book Real World Cryptography)
The latter two I don't care that much. Integration with email is doomed from my point of view. And there's just not way to have forward secrecy if we want a near-stateless system.
Email is insecure. Even with PGP, it’s default-plaintext, which means that even if you do everything right, some totally reasonable person you mail, doing totally reasonable things, will invariably CC the quoted plaintext of your encrypted message to someone else (we don’t know a PGP email user who hasn’t seen this happen). PGP email is forward-insecure. Email metadata, including the subject (which is literally message content), are always plaintext. (Thomas Ptatcek)
OK so what can I advise to my readers? What are the alternatives out there?
For file signing, Frank Denis wrote minisign which looks great.
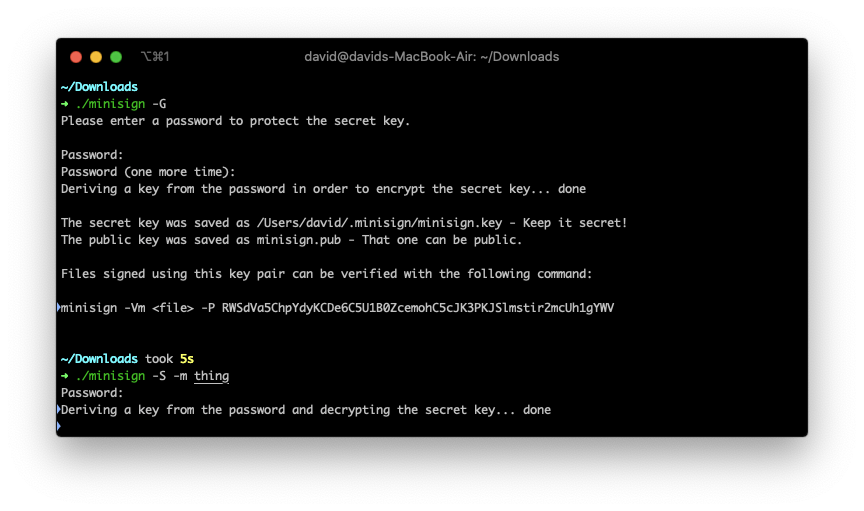
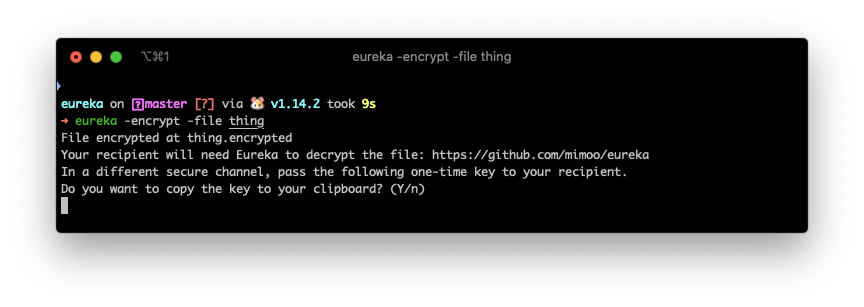
For file encryption, I wrote eureka which does the job.
There's also magic wormhole which is often mentioned, and does some really interesting cryptography, but does not seem to address a real use-case (in my opinion) for the following reason: it's synchronous. We already have a multitude of asynchronous ways to transfer files nowadays (dropbox, google drive, email, messaging, etc.) so the problem is not there. Actually there's really no problem... we just all need to agree on one way of encrypting a file and eureka does just that in a hundred lines of code.
(There is a use-case for synchronous file transfer though, and that's when we're near by. Apple's airdrop is for that.)
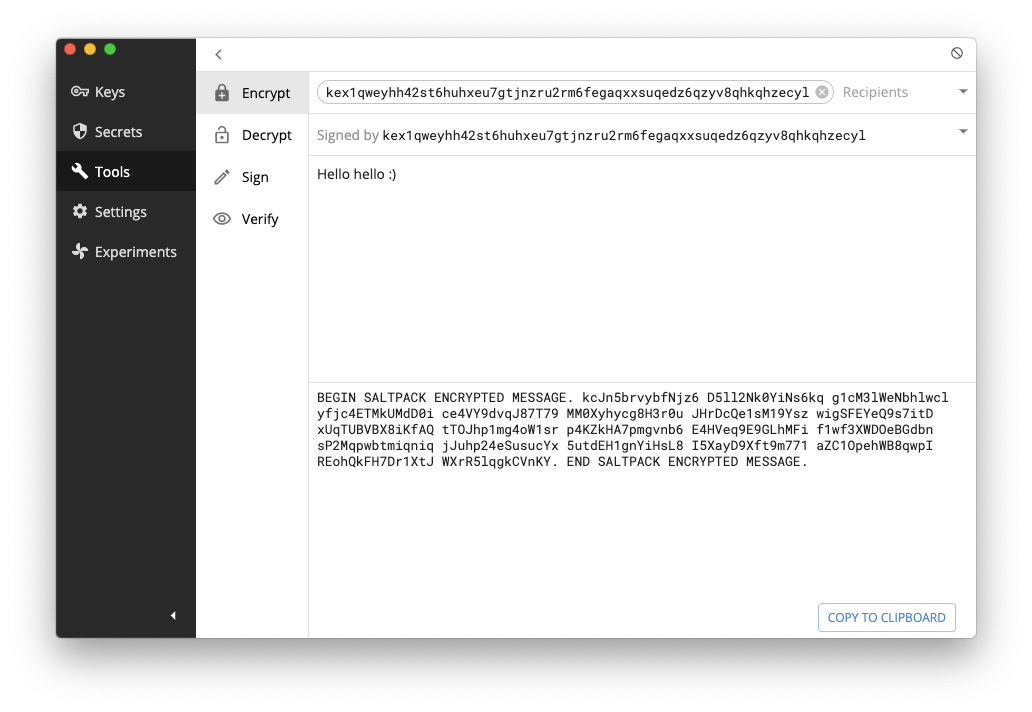
For one-time authenticated messaging (some people call that signcryption) which is pretty much the whole use-case of PGP, there seems to be only one contender so far: saltpack. The format looks pretty great and seems to address all the issues that PGP had (except for forward secrecy, but again I don't consider this a deal breaker). It seems to only have two serious implementations: keybase and keys.pub. Keybase a bit more involved, and keys.pub is dead simple and super well put.
Note that age and rage (which are excellent engineering work) seem to try to address this use case. Unfortunately they do not provide signing as Adam Caudill pointed out. Let's keep a close eye on these tools though as they might evolve in the right direction.
To obtain public keys, the web of trust (signing other people keys) hasn't been proven to really scale, instead we are now in a different key distribution model where people broadcast their public keys on various social networks in order to instill their identity to a specific public key. I don't think there's a name for it... but I like to call it broadcast of trust.
For encrypted communications, Signal has clearly succeeded as a proprietary solution, but everyone can benefit from it by using other messaging apps like WhatsApp and Wire or even federated protocols like Matrix. Matrix' main implementation seems to be Riot which I've been using and really digging so far. It also looks like the French government agrees with me.
Same thing here, the web of trust doesn't seem to work, and instead what seems to be working is relying on centralized key distribution servers and TOFU but verify (trust the first public key you see, but check the fingerprint out-of-band later).

This is end of my blog post series on cryptography with hardware.
I’ve written about smart cards and secure elements in part 1 and about HSMs and TPMs in part 2.
Trusted Execution Environment (TEE)
So far, all of the hardware solutions we’ve talked about have been standalone secure hardware solutions (with the exceptions of smart cards which can be seen as tiny computers).
Secure elements, HSMs, and TPMs can be seen as an additional computer.

(picture taken from The right secure hardware for your IoT deployment)
Let’s now talk about integrated secure hardware!
Trusted Execution Environment (TEE) is a concept that extends the instruction set of a processor to allow for programs to run in a separate secure environment. The separation between this secure environment and the ones we are used to deal with already (often called “rich” execution environment) is done via hardware. So what ends up happening is that modern CPUs run both a normal OS as well as a secure OS simultaneously. Both have their own set of registers but share most of the rest of the CPU architecture (and of course system). By using clever CPU-enforced logic, data from the secure world cannot be accessed from the normal world.
Due to TEE being implemented directly on the main processor, not only does it mean a TEE is a faster and cheaper product than a TPM or secure element, it also comes for free in a lot of modern CPUs.
TEE like all other hardware solutions has been a concept developed independently by different vendors, and then a standard trying to play catch up (by Global Platform).
The most known TEEs are Intel’s Software Guard Extensions (SGX) and ARM’s TrustZone. But there are many more like AMD PSP, RISC-V MultiZone and IBM Secure Service Container.
By design, since a TEE runs on the main CPU and can run any code given to it (in a separate environment called an “enclave”), it offers more functionality than secure elements, HSMs, TPMs (and TPM-like chips).
For this reason TEEs are used in a wilder range of applications. We see it being used in clouds when clients don’t trust servers with their own data, multi-party computation (see CCF), to run smart contracts.
TEE’s goal is to first and foremost thwart software attacks. While the claimed software security seems to be really attractive, it is in practice hard to segregate execution while on the same chip as can attest the many software attacks against SGX:
Trustzone is not much better, Quarkslab has a list of paper successfully attacking it as well.

(picture taken from Certification of the Trusted Execution Environment – one step ahead for secure mobile devices)
In theory a TPM can be re-implemented in software only via a TEE (which was done by Microsoft) but one must be careful as again, TEE as a concept provides no resistance against hardware attacks besides the fact that things at this microscopic level are way too tiny and tightly packaged together to analyze without expensive equipment. But by default a TEE does not mean you’ll have a secure internal storage (you need to have a fused key that can’t be read to encrypt what you want to store), or a hardware random number generator, and other wished hardware features. But every manufacturers sure has different offers with different levels of physical security and tamper resistance when it comes to chip that supports TEE.
Hardware Security Tokens
Finally, hardware security tokens are keys that you can usually plug into your machine and that can do some cryptographic operations. For example yubikeys are small dongles that you can plug in the USB port of a laptop, and that will perform some cryptographic operations if you touch its yellow ring.

The word “token” in hardware security token comes from the fact that using it produces a “token” per-authentication request instead of sending the same credentials over and over again.
Yubikeys started as a way to provide 2nd factor authentication, usually in addition to a password, which an attacker can’t exploit in a phishing attack. The idea is that if an attacker calls your grandmother, and asks her to spell out the yubikey output, she won’t be able to. There is no output. Furthermore, modern yubikeys implement the FIDO 2 protocol which will not produce the correct response unless you are on the right webpage (if we are talking about usage for the web). The reason is that the protocol signs metadata that is linked to what’s in the url bar of your browser.
More recently laptops and mobile devices have started offering other ways to provide the same value as a hardware security token via their own secure module. For example Apple provides a biometric-protected (Touch ID or Face ID) authenticator via the secure enclave.
It’s not clear how much protection against hardware attacks your typical hardware security token has to implement since the compromise of one is not enough to authenticate as a user in most cases (unless you use one as single factor authentication). Yet yubikeys are known to have secure elements inside. Still, this doesn’t exclude software attacks if badly programmed.
For example in 2013, a low-cost and non-intrusive side-channel attack managed to extract keys from a yubikey.
Cryptocurrency has similar dongles that will sign transactions for a user, but the threat model is different and they will usually have to authenticate the user in some ways and provide tamper resistance. Here is a picture of a Nano ledger.

As with any hardware solutions, attacks have been found there as well (for example one the trezor).
Conclusion
As a summary, this 3-part blog series surveys different techniques that exist to deal with physical attacks:
- Smart cards are microcomputers that needs to be turned on by an external device like a payment terminal. They can run arbitrary java applications. Bank cards are smart cards for example.
- Secure elements are a generalization of smart cards, which rely on a set of Global Platform standards. SIM Cards are secure elements for example.
- TPMs are re-packaged secure elements plugged on personal and enterprise computers’ motherboards. They follow a standardized API (by the Trusted Computing Group) that are used in a multitude of ways from measured/secure boot with FDE to remote attestation.
- HSMs can be seen as external and big secure elements for servers. They’re faster and more flexible. Seen mostly in data centers to store keys.
- TEEs like TrustZone and SGX can be thought of secure elements implemented within the CPU. They are faster and cheaper but mostly provide resistance against software attacks unless augmented to be tamper-resistant. Most modern CPUs ship with TEEs and various level of defense against hardware attacks.
- Hardware Security Tokens are dongles like yubikeys that often repackage secure elements to provide a 2nd factor by implementing some authentication protocol (usually TOTP or FIDO2).
- There are many more that I haven’t talked about. In reality vendors can do whatever they want. We’ve seen a lot of TPM-like chips. Apple has the secure enclave, Google has Titan, Microsoft has Pluton, Atmel for example sells “crypto elements”.
Keep in mind that no hardware solution is the panacea, you're only increasing the attack's cost. Against a sophisticated attacker all of that is pretty much useless. For this reason design your system so that one device compromised doesn't imply all devices are compromised. Even against normal adversaries, compromising the main operating system often means that you can make arbitrary calls to the secure element. Design your protocol to make sure that the secure element doesn't have to trust the caller by either verifying queries, or relying on an external trusted part, or by relying on a trusted remote party, or by being self-contained, etc. And after all of that, you still have to worry about side channel attacks :)
PS: thanks to Gabe Pike for the many discussions around TEE!
In the previous post (part 1) you learned about:
- The threat today is not just an attacker intercepting messages over the wire, but an attacker stealing or tampering with the device that runs your cryptography. So called Internet of Things (IoT) devices often run into this type of threats and are by default unprotected against sophisticated attackers.
- Hardware can help protect cryptography applications in highly-adversarial environment. One of the idea is to provide a device with a tamper-resistant chip to store and perform crypto operations. That is, if the device falls in the hands of an attacker, extracting keys or modifying the behavior of the chip will be hard. But hardware-protected crypto is not a panacea, it is merely defense-in-depth, effectively slowing down and increasing the cost of an attack.
- smart cards were one of the first such secure microcontroller that could be used as a micro computer to store secrets and perform cryptographic operations with them. These are supposed to use a number of techniques to discourage physical attackers.
- the concept of a smart card was generalized as a secure element, which is a term employed differently in different domains, but boils down to a smart card that can be used as a coprocessor in a greater system that already has a main processor.
- Google having troubles dealing with the telecoms to host credit card information on SIM cards (which are secure elements), the concept of secure element in the cloud was born. In the payment space this is called host card emulation (HCE). It works simply by storing the credit card information (which is a 3DES symmetric key shared with the bank) in a secure element in the cloud, and only giving a single-use token to the user: if the phone is compromised, the attacker can only use it to pay once.
All good?
In this part 2 of our blog series you will learn about more hardware that supports cryptographic operations! These are all secure elements in concept, and are all doing sort of the same things but in different contexts. Let’s get started!
Hardware Security Module (HSM)
If you understood what a secure element was, well a hardware secure module (HSM) is pretty much a bigger secure element.
Not only the form factor of secure elements require specific ports, but they are also slow and low on memory. (Note that being low on memory is sometimes OK, as you can encrypt keys with a secure element master key, and then store the encrypted keys outside of the secure element.)
So HSM is a solution for a more portable, more efficient, more multi-purpose secure element. Like some secure elements, some HSMs can run arbitrary code as well.
HSMs are also subject to their own set of standards and security level. One of the most widely accepted standard is FIPS 140-2: Security Requirements for Cryptographic Modules, which defines security levels between 1 and 4, where level 1 HSMs do not provide any protection against physical attacks and level 4 HSMs will wipe their whole memory if they detect any intrusion!
Typically, you find an HSM as an external device with its own shelf on a rack (see the picture of a luna HSM below) plugged to an enterprise server in a data center.

(To go full circle, some of these HSMs can be administered using smart cards.)
Sometimes you can also find an HSM as a PCIe card plugged into a server’s motherboard, like the IBM Crypto Express in the picture below.

Or even as small dongles that you can plug via USB (if you don’t care about performance), see the picture of a YubiHSM below.

HSMs are highly used in some industries. Every time you enter your PIN in an ATM or a payment terminal, the PIN ends up being verified by an HSM somewhere. Whenever you connect to a website via HTTPS, the root of trust comes from a Certificate Authority (CA) that stores its private key in an HSM, and the TLS connection is possibly terminated by an HSM. You have an Android or iPhone? Chances are Google or Apple are keeping a backup of your phone safe with a fleet of HSMs. This last case is interesting because the threat model is reversed: the user does not trust the cloud with its data, and thus the cloud service provider claims that its service can’t see the user’s encrypted backup nor can access the keys used to encrypt it.
HSMs don’t really have a standard, but most of them will at least implement the Public-Key Cryptography Standard 11 (PKCS#11), one of these old standards that were started by the RSA company and that were progressively moved to the OASIS organization (2012) in order to facilitate adoption of the standards.
While PKCS#11 last version (2.40) was released in 2015, it is merely an update of a standard that originally started in 1994. For this reason it specifies a number of old cryptographic algorithms, or old ways of doing things. Nevertheless, it is good enough for many uses, and specifies an interface that allow different systems to easily interoperate with each other.
While HSMs’ real goals are to make sure nobody can extract key material from them, their security is not always shining.
A lot about the security of these hardware solutions really relies on their high price, the protection techniques used not being disclosed, and the certifications (like FIPS and Common Criteria) mostly focusing on the hardware side of things. In practice, devastating software bugs have been found and it is not always straight forward to know if the HSM you use is vulnerable to any of these vulnerabilities (Cryptosense has a good summary of known attacks against HSMs).
By the way, not only the price of one HSM is high (it can easily be dozens of thousands of dollars depending on the security level), in addition to an HSM you often have another HSM you use for testing, and another one you use for backup (in case your first HSM dies with its keys in it). It can add up!
Furthermore, I still haven’t touched on the elephant in the room with all of these solutions: while you might prevent most attackers from reaching your secret keys, you can't prevent attackers from compromising the system and making their own calls to the secure hardware module (be it a secure element or an HSM). Again, these hardware solutions are not a panacea and depending on the scenario they provide more or less defense-in-depth.
By the way, if it applies to your situation modern cryptography can offer better ways of reducing the consequences of key material compromise and mis-use. For example using multi-signatures! Check my blog post on the subject.
Trusted Platform Module (TPM)
A Trusted Platform Module (TPM) is first and foremost a standard (unlike HSMs) developed in the open by the non-profit Trusted Computing Group (TCG).
The latest version is TPM 2.0, published with the ISO/IEC (International Organization for Standardization and the International Electrotechnical Commission).
A TPM complying with the TPM 2.0 standard is a secure microcontroller that carries a hardware random number generator also called true random number generator (TRNG), secure memory for storing secrets, cryptographic operations, and the whole thing is tamper resistant.
If this description reminds you of smart cards, secure element, and HSMs well… I told you that everything we were going to be talking about in this chapter were going to be secure elements of some form. (And actually, it’s common to see TPMs implemented as repackaging of secure elements.)
You usually find a TPM directly soldered to the motherboard of many enterprise servers, laptops, and desktop computers (see picture below).

Unlike solutions that we’ve seen previously though, a TPM does not run arbitrary code. It offers a well-defined interface that a greater system can take advantage of. Due to these limitations, a TPM is usually pretty cheap (even cheap enough that some IoT devices will ship with one!).
Here is a non-exhaustive list of interesting applications that a TPM can enable:
- User authentication. Ever heard of the FBI iPhone fiasco? TPMs can be used to require a user PIN or password. In order to prevent low entropy credentials to be easily bruteforced, a TPM can rate limit or even count the number of failed attempts.
- Secure boot. Secure boot is about starting a system in a known trusted state in order to avoid tampering of the OS by malware or physical intrusion. This can be done by using a platform’s TPM and the Unified Extensible Firmware Interface (UEFI) which is the piece of code that launches an operating system. Whenever the image of a new boot loader or OS or driver is loaded, the TPM can store the associated expected hash and compare it before running the code, and failing if the hash of the image is different. If you hold a public key you can also verify that a piece of code has been signed before running it. This is a gross over-simplification of how secure boot works in practice, but the crypto is pretty straight forward.
- Full disk encryption (FDE). This allows to store the key (or encrypt the key) that encrypts all data on the device at rest. If the device has been proven to be in a known good state (via secure boot) and the user authenticates correctly, the key can be released to decrypt data. When the devices is locked or shut down, the key vanishes from memory and has to be released by the TPM again. This is a must feature if you lose, or get your device stolen.
- Remote attestation. This allows a device to authenticate itself or prove that it is running specific software. In other words, a TPM can sign a random challenge and/or metadata with a key that can be tied to a unique per-TPM key (and is signed by the TPM vendor). Every TPM comes with such a unique key (called an endorsement key) along with the vendor’s certificate authority signature on the public key part. For example, during employee onboarding a company can add a new employee’s laptop’s TPM endorsement key to a whitelist of approved devices. Later, if the user wants to access one of the company’s service, the service can request the TPM to sign a random challenge along with hashes of what OS was booted to authenticate the user and prove the well-being of the user’s device.
There are more functionalities that a TPM can enable (there's afterall hundreds of commands that a TPM implements) which might even benefit user applications (which should be able to call the TPM).
Note that having a standard is great for inter-operability, and for us to understand what is going on, but unfortunately not everyone use TPMs. Apple has the secure enclave, Microsoft has Pluton, Google has Titan.
Perhaps, on a darker note, it is good to note that TPMs have their own controversies and have also been subjected to devastating vulnerabilities. For example the ROCA attack found that an estimated million TPMs (and even smart cards) from the popular Infineon vendor had been wrongly generating RSA private keys for years (the prime generation was flawed).
To recap, you’ve learned about:
- HSMs. They are external, bigger and faster secure elements. They do not follow any standard interface, but usually implement the PKCS#11 standard for cryptographic operations. HSMs can be certified with different levels of security via some NIST standard (FIPS 140-2).
- TPMs. They are chips that follow the TPM standard, more specifically they are a type of secure element with a specified interface. A TPM is usually a secure chip directly linked to the motherboard and perhaps implemented using a secure element. While it does not allow to run arbitrary programs like some secure elements, smart cards, and HSMs do, it enables a number of interesting applications for devices as well as user applications.
That’s it for now, check this blog again to read part 3 which will be about TEEs!
Many thanks to Jeremy O'Donoghue, Thomas Duboucher, Charles Guillemet, and Ryan Sleevi who provided help and reviews!



























