Last time I wrote about TLS pre-master keys and master keys.
I just realized one more thing in TLS that doesn't make sense (besides the fact that different versions of TLS have different PRFs). Here's RFC 5246 (the RFC on TLS 1.2) on how to use the PRF transform your pre-master key into a master key:

Here's the same RFC on how to use the PRF to transform your master key into your 4 or 6 keys:

Noticed anything?
Took me some time, the first takes the server random appended to the client random, while the second takes the client random appended to the server random. I'm willing to bet this is not to circumvent any attack but rather to confuse the implementer...
Everything you want to know about TLS 1.2 is in RFC 5246. But as you may know, if you've read RFCs before, it is not easy to parse (plus they have some sort of double spaces non-sense).
Before we can encrypt/MAC everything with keys to secure our connection, we need to go over a key exchange called the Handshake to safely agree on a set of keys for both parties to use. The handshake can currently use 5 different algorithms to do the key exchange: RSA, Diffie-Hellman, Elliptic Curve Diffie-Hellman and the ephemeral versions of the last two algorithms.
This blogpost is about what happens between this key exchange and the encryption/authentication of data.
The Pre-Master Secret
The pre-master key is the value you directly obtain from the key exchange (e.g. \(g^{ab} \pmod{p}\) if using Diffie-Hellman). Its length varies depending on the algorithm and the parameters used during the key exchange. To make things simpler, we would want a fixed-length value to derive the keys for any cipher suite we would want to use. This is the reason behind a pre master secret. The fixed-length value we'll call master secret. Here the RFC tells us how to compute it from the pre-master secret after having removed the leading zeros bytes.
master_secret = PRF(pre_master_secret, "master secret",
ClientHello.random + ServerHello.random)
[0..47];
The two random values ClientHello.random and ServerHello.random, sometimes called "nonces", are randomly generated and sent during the ClientHello of each parties. This is to bound the soon-to-be master key to this session. PRF stands for Pseudo-random function, basically some concrete construction that emulates a random oracle: given an input will produce an output computationally indistinguishable from a truly random sequence. But let's move on, and we will see later what exactly is that PRF.
The Master Secret
A master secret is always 48 bytes. So now that we have a fixed length value, we can derive 4 keys from it:
- client_write_MAC_key
- server_write_MAC_key
- client_write_key
- server_write_key
As you can probably guess, MAC keys are for the authentication and integrity with whatever MAC algorithm you chose in the cipher suite, write keys are for the symmetric encryption.
Interestingly, two keys are generated for every purpose: one key per side. This is mostly by respect of good practices. Always segregate the use of your keys.
The symmetric ciphers chosen in the handshake will dictate how long these keys we generate need to be. Note that AEAD ciphers that combine both authentication and encryption will not need MAC keys but will need two other keys instead: client_write_IV and server_write_IV. This is because their MAC keys are directly derived from the encryption keys.
The same PRF we used on the pre-master key will be used on the master-key over and over until enough bytes have been created for the keys. From the section 6.3 of the RFC:
key_block = PRF(SecurityParameters.master_secret,
"key expansion",
SecurityParameters.server_random +
SecurityParameters.client_random);
The key_block value is then cut into enough keys.
That's it! Here's a recap:
Diffie-Hellman -> pre-master key -> 48bytes master key -> 4 variable-length keys.
The PRF
OK. Now that we got a nice global view of the process, let's dig deeper. The PRF used in TLS 1.2 is discussed here. It is quite different from the PRF used in TLS 1.1, see here.
Remember, for example how it was used to transform the pre-master key into a master key:
master_secret = PRF(pre_master_secret, "master secret",
ClientHello.random + ServerHello.random)
[0..47];
This is how the PRF function is used:
PRF(secret, label, seed) = P_<hash>(secret, label + seed)
If you want to follow along with code, here's the relevant golang code
P_hash(secret, seed) = HMAC_hash(secret, A(1) + seed) +
HMAC_hash(secret, A(2) + seed) +
HMAC_hash(secret, A(3) + seed) + ...
where + indicates concatenation, A() is defined as:
A(0) = seed
A(i) = HMAC_hash(secret, A(i-1))
This was a copy/paste from the RFC. To make it clearer: We use the label string ("master secret" in our example) concatenated with the two peers' random values as a seed.
We then MAC the seed with our pre-master secret as the key. We use the first output. Iterating the MAC gives us the subsequent values that we can append to our output.
\[ u_0 = label + serverHello.random + clientHello.random \]
\[ u_i = HMAC(secret, u_{i-1}) \]
\[ output = u_1 , u_2 , \cdots \]
This goes on and on until the output is long enough to cover the 48 bytes of the master key (or the 4 keys if we're applying to PRF on the master key).
If P_256 is being used, then SHA-256 is being used. This means the output of HMAC will be 256 bits (32 bytes). To get the 48 bytes of the master key, two iterations are enough, and the remaining bytes can be discarded.
I'm doing some tests on how Pollard Rho performs. I implemented the thing in Sage here and it doesn't perform that well I found. Pollard Kangaroo is also bad, but that must come from my implementation (I didn't really go further here since I don't really need Kangaroo: I already know the order + the value I'm looking for is not in any particular interval)
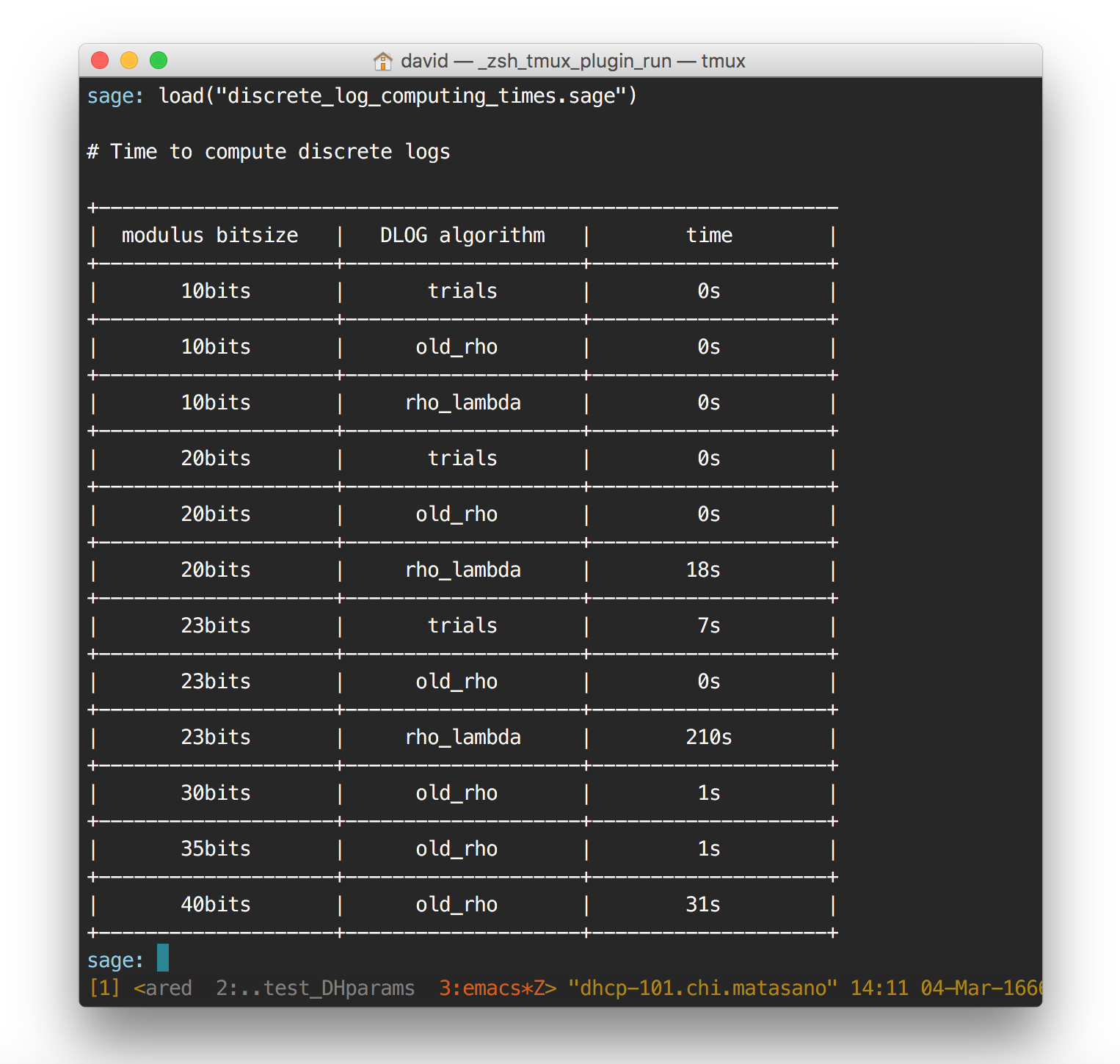
old_rho is Pollard rho, rho_lambda is the mislabeled Pollard Kangaroo algorithm, trials is the simple enumeration.
I implemented the algorithm in Go, along some nice functions/variables that make Go's bignumber library a bit easier to tolerate. And guess what? What takes Sage 63 seconds to compute only take Go 5 seconds. The implementation is a copy/paste of what I did in Sage, no optimizations.
There is a new attack on OpenSSL. It's called DROWN.

Two problems:
-
in OpenSSL versions prior to January of this year, SSLv2 is by default not disabled. They thought that removing all the SSLv2 cipher suites from the default cipher string (back in 2010) would work but... nope. Even if not advertised in the serverHello, you can still do a handshake with whatever SSLv2 cipher you want. Another way of completely disabling SSLv2 exists, but it's recent and it is not the default option.
- A padding oracle attack still exists in SSLv2. This is because of the export cipher suites. These weak ciphers and key lengths the USA government was forcing on OpenSSL so that people overseas could use it. So, these export cipher suites, nowadays they are bruteforce-able. It takes a few hours though, and a few hundred dollars, so no easy active MITM. It's a rather passive attack.
This is a cross-protocol attack. This means that you are a MITM, but you leave the client doing his thing on a TLS 1.2 or whatever SSLv3+ protocol. In the mean time though, you use the SSLv2 connection as an Oracle to recover the premaster-key (and thus the session key that is derived from it).
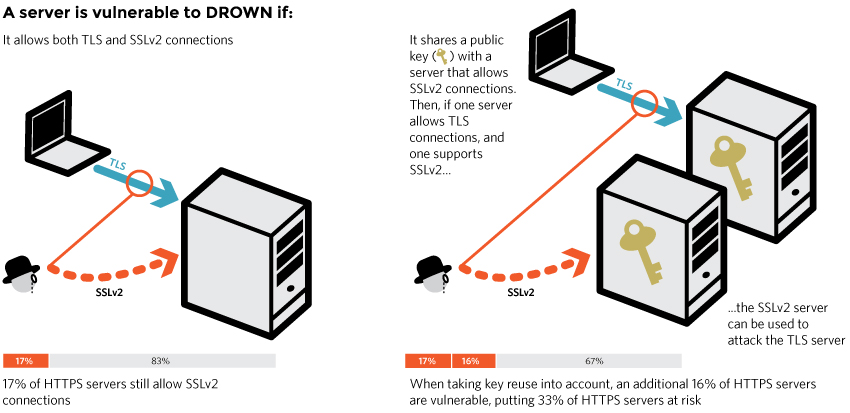
Three things:
-
The attack works on RSA handshakes. In the handshake (precisely in the clientKeyExchange) the client will encrypt his premaster-key with the server's RSA public key, this is what the attack decrypts. The server doesn't support RSA handshakes? You'll have to attack another server.
-
The server doesn't have to work with SSLv2. If another server (could even be a mail server) sharing the same RSA key and supporting SSLv2 exists, then you can use it as your oracle during the attack! Practical much?
- To use the oracle, you need to first transform the RSA encrypted premaster-key into a valid SSLv2 RSA encrypted master-key. It is quite different, because of protocol differences, and you need to use quite a few tricks (trimmers!). It doesn't work all the time, around 1 out of 1,000 RSA encrypted premaster-key can be decrypted. This is often more than enough to steal the cookies and have consequences. If you're targeting a specific individual it can take time though, so to speed up these 1,000 handshakes just inject some javascript in a non-https webpage!
That's pretty much everything. I'm still going through the paper, trying to understand the math. There is a tool here to test your website. Another way of doing this (especially for internal servers) is to get an openssl version prior to january this year and do that on all of your subdomains/domains: openssl s_client -ssl2 -connect www.cryptologie.net:443
A few weeks ago, NIST released a draft on their report on Post-Quantum Cryptography.
As we all know, some things are happening in the quantum computing world. Some are saying it will never work, some are saying it will but that it will take time until large enough quantum computers could break today's crypto.
So reading this paragraph taken from the NIST document, it can make sense on why we would want to move today to post-quantum crypto:
Historically, it has taken almost 20 years to deploy our modern public key cryptography infrastructure. It will take significant effort to ensure a smooth and secure migration from the current widely used cryptosystems to their quantum computing resistant counterparts. Therefore, regardless of whether we can estimate the exact time of the arrival of the quantum computing era, we must begin now to prepare our information security systems to be able to resist quantum computing.
Let's see where is this number coming from. SSL/TLS, its protocol or its implementation, its coverage or its efficiency, has been a huge mess so far:
-
In 2009, 7 years ago, moxie introduced SSLStrip at Blackhat, a technique to render https completely useless without preloaded HSTS.
-
It's only in 2013, 3 years ago, that facebook finally made the whole app https-only just blows my mind. And that's not thinking of the myriad of companies, commerce, banks and other websites that were all accessible through http back then.
-
Nowdays most websites are still vulnerable to moxie's 2009 attack. Think about it, TLS is supposed to protect the communications against a passive and an active attacker on the network. In the passive case, I think it succeeded (in most cases). In the active case? Even HSTS or HPKP can still be somehow circumvented. Only browsers are fully capable of protecting us nowadays.
- And this is ignoring all the horrible implementations flaws like heartbleed, the broken cert validations of browsers, the broken basicConstraints of most CAs...
We could also talk about the deprecation of md5 and sha1, but sleevi does that better than me:
-
1996, 20 years ago, researches recommend to switch from md5 to sha1 because of recent advances.
-
2013, 17 years after the recommendation, Apple finally removes its support for MD5 in certificates.
- We're still in the middle of deprecating sha1, and it's a mess.
(there's also a graphical timeline made by ange: here)
Or what about the deprecation of DES? Or RC4? Or 1024 bit DH? ..
To come back to the NIST's report, here's a nice table of the impact of quantum computing on today's algorithms:
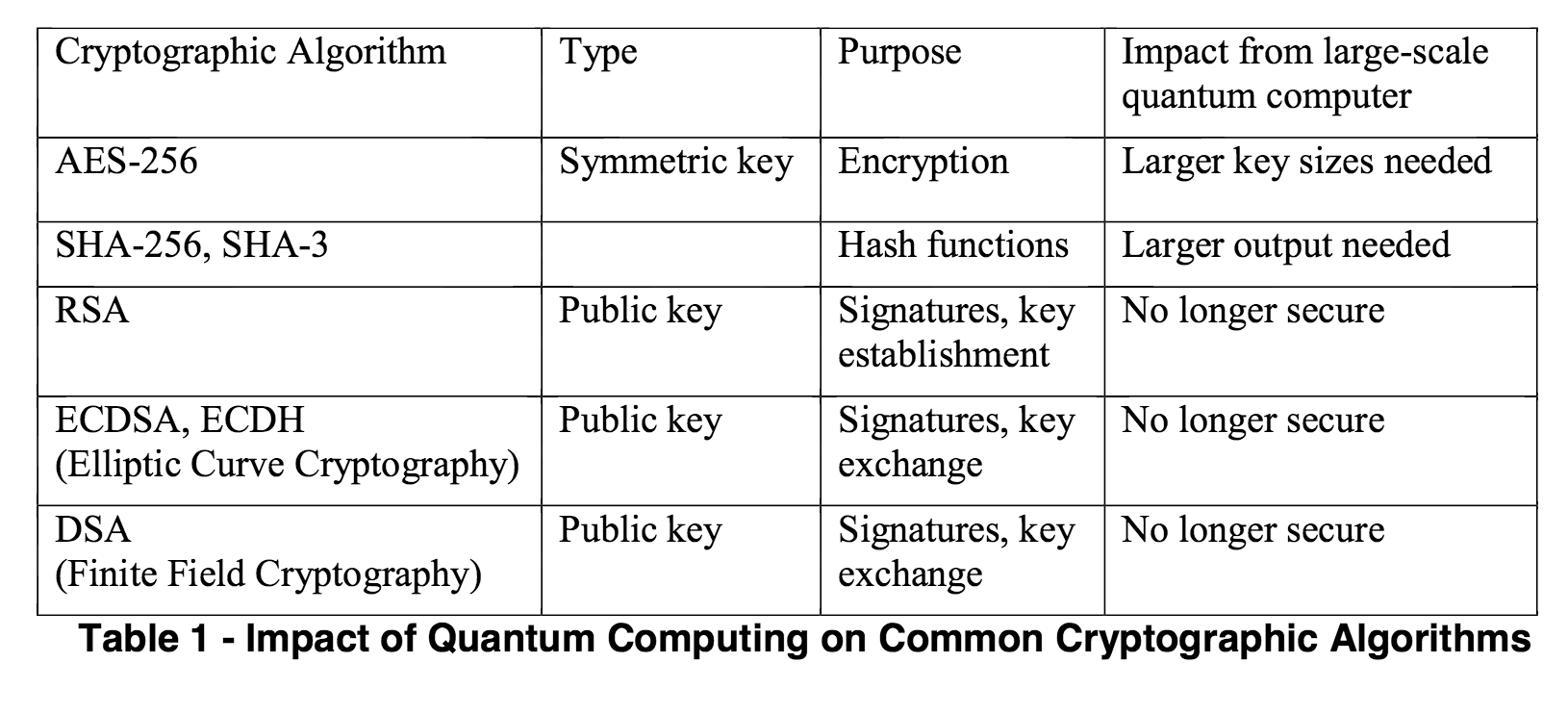
sums up pretty well what djb wrote:
Imagine that it's fifteen years from now. Somebody announces that he's built a large quantum computer. RSA is dead. DSA is dead. Elliptic curves, hyperelliptic curves, class groups, whatever, dead, dead, dead.
Contrarily to the european initiative PQCrypto, they seem to imply that they will recommend lattice-based crypto whenever their new suite B will be done. I find hard to trust any system's security proof that rely on lattice's theorical bounds because as it is known with LLL, BKZ and others: practical results are way better than these theorical limits. I don't know much about lattice crypto though, and I would you out to this paper in my to read list: Lattice-based crypto for beginners.
They agree on Hash-based signatures (which are explained in a 4 posts series on my blog), which is timy because a new version of the RFC draft for XMSS has came out, which might be the most polished hash-based signature system out there (although it is stateful unlike SPHINCS).
The paper ends on these wise words that explains how security estimation works (and has always worked):
We note that none of the above proposals have been shown to guarantee security against all quantum attacks. A new quantum algorithm may be discovered which breaks some of these schemes. However, this is similar to the state today. Although most public-key cryptosystems come with a security proof, these proofs are based on unproven assumptions. Thus the lack of known attacks is used to justify the security of public-key cryptography currently in use.
To talk about quantum computing advances, I don't know much about it but here are some notes:
-
Shor’s algorithm (the one that breaks everything) was born on 1994.
-
Late 1990s, error correcting codes and threshold theorems for quantum computing. Quantum computing might be possible?
-
2011, "the world's first commercially available quantum computer" is released by D-Wave. I believe this angered many people because this wasn't really quantum computing.
- 2015, Google and NASA have D-wave computers.
To finish this blogpost, a few things I remember from last month Real World Crypto conference:
There is definitely a skepticism in the crypto world about quantum computing, as there is a gold rush into designing new post-quantum crypto.